28.Трение.Сила трения скольжения. Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.В первом приближении величина силы трения скольжения может быть рассчитана по формуле:

, где  — коэффициент трения скольжения,  — сила нормальной реакции опоры.

По физике взаимодействия трение принято разделять на:

• Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя.

• Сухое с сухой смазкой (графитовым порошком)

• Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;

• Смешанное, когда область контакта содержит участки сухого и жидкостного трения;

Граничное, когда в области контакта могут содержатся слои и участки различной природы (окисные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения. Конусом трения называют конус, описанный предельной силой реакции шероховатой связи вокруг направления нормальной реакции.

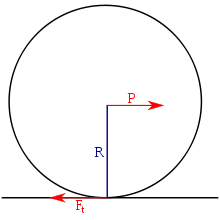
Если к телу, лежащему на шероховатой поверх­ности, приложить силу Р, образующую угол с нор­малью (рис. 27), то тело сдвинется только тогда, когда сдвигающее усилие будет больше 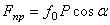(мы считаем , пренеб­регая весом тела). Но неравенство , в котором , выполняется только при , т.е. при . Следовательно, ни­какой силой, образующей с нормалью угол , меньший угла трения , тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или само­торможения тел.

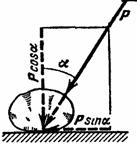Рис.27Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

29.Трение качения.Коэффициент качения.Момент качения. Тре́ние каче́ния — сопротивление движению, возникающее при перекатывании тел друг по другу. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном. В большинстве случаев величина трения качения гораздо меньше величины трения скольжения при прочих равных условиях, и потому качение является распространенным видом движения в технике. Сила трения качения 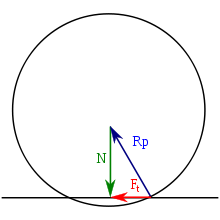Рис. 1.  — реакция опоры;  — прижимающая сила;  — сила трения качения,  — внешняя сила (приложена к центру тела и направлена вправо, на рисунке не показана); сумма векторов сил Пусть на тело вращения, располагающееся на опоре, действуют

• P — внешняя сила, пытающаяся привести тело в состояние качения или поддерживающая качение и направленная вдоль опоры;

• N — прижимающая сила;

•  — реакция опоры.

Если векторная сумма этих сил равна нулю

то ось симметрии тела движется равномерно и прямолинейно или остаётся неподвижной (см. рис. 1). Вектор определяет силу трения качения, противодействующую движению. Это означает, что прижимающая сила уравновешивается вертикальной составляющей реакции опоры, а внешняя сила уравновешивается касательной составляющей реакции опоры.

Ри с. 2.  — внешняя сила;  — сила трения качения; R — радиус тела вращения; Равномерное качение означает также, что сумма моментов сил относительно произвольной точки равна нулю. Из равновесия относительно оси вращения моментов сил, изображённых на рис. 2 и 3, следует:

откуда где

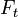•  — сила трения качения;

• f — коэффициент трения качения, имеющий размерность длины (следует отметить важное отличие от коэффициента трения скольжения, который безразмерен);

• R — радиус катящегося тела;

• N — прижимающая сила.

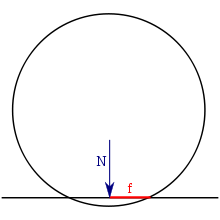
Рис. 3. Момент силы трения действующий против часовой стрелки (относительно мгновенного центра вращения в зоне контакта — правого конца отрезка f) и тормозящий качение тела вправо; N — прижимающая сила; f — коэффициент трения качения, равный длине плеча силы N.

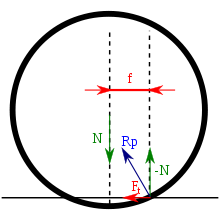Рис. 4. Коэффициент трения f;  — асимметричная реакция опорной поверхности, векторная сумма вертикальной и горизонтальной компонент;  — прижимающая сила;  — сила трения качения.

Эта зависимость подтверждается экспериментально. Для малой скорости качения сила трения качения не зависит от величины этой скорости. Когда скорость качения достигает значений, сопоставимых со значениями скорости деформации в материале опоры, трение качения резко возрастает и даже может превысить трение скольжения при аналогичных условиях.

Момент сил трения качения.Определим для подвижного цилиндра момент, тормозящий вращательное движение тела. Рассматривая данный момент относительно оси вращающегося колеса (например, колеса автомобиля), находим, что он равен произведению тормозного усилия на оси на радиус колеса. Относительно точки контакта движущегося тела с землей момент будет равен произведению внешней силы, уравновешивающей силу трения, на радиус колеса (рис. 2): .С другой стороны, момент трения равен моменту прижимающей силы на плечо, длина которого равна коэффициенту трения качения f: где

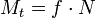•  — момент силы трения в [Н] · [м];

• R — радиус тела качения;

• P — внешняя сила;

•  — сила трения качения;

• f — коэффициент трения качения в [м].

Коэффициент трения качения

Из выписанного выше уравнения следует, что коэффициент трения качения может быть определен как отношение момента трения качения к прижимной силе N:

Графическая интерпретация коэффициента трения качения f дана на рис. 3 и 4.Коэффициент трения качения имеет следующие физические интерпретации:

• Если тело находится в покое и внешняя сила отсутствует, то реакция опоры лежит на той же линии, что и прижимающая сила. Когда тело катится, то из условия равновесия следует, что нормальная составляющая реакции опоры параллельна и противонаправлена прижимающей силе, но не лежит с ней на одной линии. Коэффициент трения качения равен расстоянию между прямыми, вдоль которых действуют прижимающая сила и нормальная составляющая реакции опоры (рис. 4).

• Движение катящегося тела без проскальзывания можно рассматривать как поворот вокруг мгновенной оси вращения (на рис. 4 — точка приложения вектора ), которая для абсолютно твёрдых тел совпадает с основанием перпендикуляра, опущенного из центра круга на опору. Для случая реальных (деформирующихся под нагрузкой) материалов мгновенный центр вращения смещён в направлении качения тела, а величина смещения равна значению коэффициента трения качения.

24.Теорема Вариньона о моменте равнодействующей. Условие равновесия рычага.В общем случае произвольная плоская система сил приводится к главному вектору F'гл и к главному моменту Mгл относительно выбранного центра приведения, причем главный момент равен алгебраической сумме моментов заданных сил относительно точки О: Было показано, что можно выбрать центр приведения, относительно которого главный момент системы будет равен нулю, и система сил приведется к одной равнодействующей , равной по модулю главному вектору . Определим момент равнодействующей относительно точки О. Учитывая, что плечо ОС силы F равно , получаем .

Две величины, порознь равные третьей, равны между собой, поэтому из предыдущих уравнений находим .

Полученное уравнение выражает теорему Вариньона: момент равнодействующей плоской системы сил относительно произвольно взятой точки равен алгебраической сумме моментов составляющих сил относительно той же точки.

Из теоремы Вариньона следует, что главный момент плоской системы сил относительно любой точки, лежащей на линии действия ее равнодействующей, равен нулю

Условие равновесия рычага

Рычагом называется твердое тело (например, стержень), которое может вращаться около неподвижной оси под действием сил, расположенных в плоскости, перпендикулярной этой оси (фиг.26). Для равновесия рычага необходимо и достаточно, чтобы сумма моментов приложенных к ему сил относительно неподвижной точки (опоры) рычага равнялась нулю. Для рычага, показанного на фиг.26, условие равновесия будет: P1h1+P2h2-P3h3=0. Условие равновесия рычага используется при определении реакций опор и решении задач на опрокидывание.

Раздел Кинематика.41,42,45,47. Способы задания движения точки.Для задания движения точки можно применять один из следую­щих трех способов: 1) векторный, 2) координатный, 3) естественный.1.       Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор , проведенный из на­чала координат О в точку М (рис. 1).

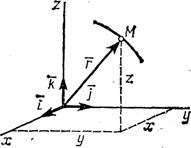Рис.1При движении точки М вектор будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, является переменным вектором (вектором-функцией), зависящим от аргу­мента : . Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор и найти положение движущейся точки. Геометрическое место концов вектора , т.е. годограф этого вектора, определяет траекторию движущейся точки.

2.       Координатный способ задания движе­ния точки. Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости , , .

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .Нетрудно установить зависимость между векторным и координатным способами задания движения.Разложим вектор на составляющие по осям координат: где - проекции вектора на оси; – единичные векторы направленные по осям, орты осей. Так как начало вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

Пример 1. Движение точки задано уравнениями 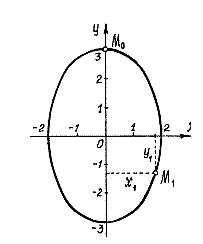Рис.Чтобы исключить время, параметр t, найдём из первого уравнения из второго Затем возведём в квадрат и сложим. Так как получим Это уравнение эллипса с полуосями 2 см и 3 см (рис.2).Начальное положение точки M₀ (при t=0) определяется координатами Через 1 сек. точка будет в положении M₁ с координатами

 3. Естественный способ задания движе­ния точки. Рис.3Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О' до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать.

44.Годограф… Годограф

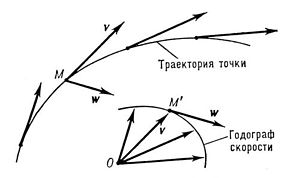Годограф скорости.Годограф (от др.-греч. ὁδός — путь, движение, направление и γράφω — пишу) в механике — кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала О (см. рис.).Понятие годографа было введено английским учёным У. Гамильтоном.Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу. Например, скорость точки является величиной, изображаемой переменным вектором v. Отложив значения, которые имеет вектор v в разные моменты времени, от начала О, получим годограф скорости; при этом величина, характеризующая быстроту изменения скорости в точке М, то есть ускорение (в этой точке), имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке М’.

51.Простейшие движения твердого тела. К простейшим движениям твердого тела относятся поступательное и вращательное.Поступательным называется движение твердого тела, при котором любая прямая, взятая в теле, остается параллельной своему начальному положению.Теорема. При поступательном движении все точки твердого тела описывают одинаковые траектории и имеют в каждый момент времени равные скорости и ускорения.

Вращательным называется движение твердого тела, при котором все точки некоторой прямой, связанной с телом, остаются неподвижными во время движения. Эта прямая называется осью вращения. (рис. 2.2.1)Положение тела определено, если задан угол  между плоскостями  и , проходящими через ось вращения (  с единичным направляющим вектором ) (рис. 2.2.1) . Плоскость  неподвижна, а плоскость  жестко связана с телом. Угол  измеряется в радианах и изменяется с течением времени,  – уравнение вращательного движения твердого тела. Угловая скорость  характеризует изменение угла поворота с течением времени. Угловое ускорение  – характеризует быстроту изменения угловой скорости.Если угловая скорость  постоянна, то вращение называется равномерным и происходит по закону . Если угловое ускорение  постоянно, то вращение называется равнопеременным и происходит согласно уравнениям: ,         .Модули скорости, ускорения, касательного, нормального ускорений точки вращающегося тела, находящейся на расстоянии  от оси вращения, определяются по формулам: , , , ,   Ускорение точки составляет угол  с направлением нормали, при этом .

54. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях.Движение груза 1 должно описываться уравнением:

,где t — время, c, c₀, c₁, c₂, — некоторые постоянные.В начальный момент времени (t = 0) положение груза определяется координатой x₀, и он имеет скорость v₀. Учесть, что в момент времени t = t₂ координата груза равна x₂.Определить коэффициенты c₀, c₁, c₂, при которых осуществляется требуемое движение груза 1. Определить также в момент времени t = t₁ скорость и ускорение груза и точки М одного из колес механизма.Схема механизма показана на рис. К2.1.

Дано: R₂ = 20 см, r₂ = 15 см, R₃ = 10 см, x₀ = 5 см, v₀ = 10 см/c, x₂ = 179 см, t₂ = 3c, t₁ = 2c.Решение. Уравнение движения груза:Уравнение скорости груза:Определение коэффициентов c₀, c₁, c₂:

При t₀ = 0, x₀ = 5 см => c₀ = 5 см; .

При t₂ = 3с, x₂ = 179 см/c² => c₂ = 16 см/с²;

При t₁ = 2с, v₁ = 74 см/c, a = 32 см/с²

Таким образом уравнение движения груза будет:

x = 16t² + 10t + 5Уравнение скорости груза:v = 72t + 5

Для определения скорости и ускорения точки М запишем уравнения, связывающие скорость груза v и угловые скорости колес ω₂ и ω₃.В соответствие со схемой механизма:Определение ускорений.Угловое ускорение колеса:Определение полного, нормального и касательного ускорений точки М.