3.2. Сложные реологические тела

При последовательном соединении элементов полная нагрузка  приходится на каждый элемент, входящий в сложное тело:

 = ₁ = ... = _n,

а полная деформация, возникающая в теле, складывается из деформаций, возникающих в отдельных составляющих сложное тело элементах: 

 = ₁ +  ... + _n.

При параллельном соединении элементов деформации одинаковы для всех элементов:

 = ₁ =  ... = _n,

а полная нагрузка  складывается из нагрузок на отдельных элементах:

 = ₁ + ... + _n.

Рассмотрим некоторые примеры построения сложных тел.

3.2.1. Упруго-пластическое тело Прандтля. Структурная формула тела Прандтля имеет вид Р  = Н — StV. Реологическая диаграмма и механическая модель этого тела приведены на рис. 9. Данное тело при напряжениях, ниже предела текучести_i <_т, деформируется упруго по закону Гука _i = G^_I , а при _i = _т деформируется пластически. У этого тела деформация при разгрузке восстанавливается лишь частично. Общая деформация сдвига ^s слагается из упругой ^e и пластической частей:

Рис. 9. Деформационная кривая тела Прандтля: _e – упругая деформация, ^p – пластическая деформация

^s = ^e + ^p.

Упругопластическое тело Прандтля представляет собой тело, у которого отсутствует деформационное упрочнение. Для поддержания развития пластической деформации не требуется повышения напряжений _i до значений, превышающих предел текучести _т: достаточно поддерживать напряжения, равные пределу текучести.

Рис. 10. Деформирование упругопластического тела,

обладающего упрочнением

На рис.10 приведена зависимость интенсивности касательных напряжений _i от интенсивности сдвиговой деформации _i для упругопластического материала, обладающего деформационным упрочнением. При деформировании такого материала за начальной величиной предела текучести _т в материале начинает накапливаться остаточная деформация ^p. Уменьшению напряжений _i на этом участке деформирования соответствует процесс разгрузки, происходящий по упругому закону (пунктирные линии а, б, в, на рис. 10). Новое повышение напряжений _i приводит к увеличению предела текучести до значения _ > _т. Это и есть упрочнение, связанное с развитием пластической деформации.

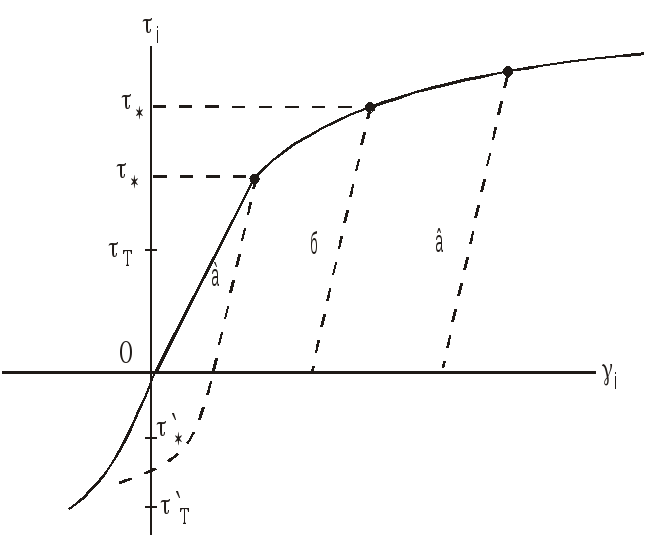
В таком материале наблюдается и эффект Баушингера: величина обратного (при растяжении материала) предела текучести (упругости) снижается _*' < _т' (рис. 10).

3.2.2. Вязкоупругое тело Максвелла, ползучесть и релаксация напряжений. Структурная формула тела Максвелла М = H — N (рис. 11 а). Реологическое уравнение, соответствующее этой структурной формуле, представляется следующим образом

_M = _H + _N,

где _H, _N – деформация элемента модели тела Гука, Ньютона. Аналогичный вид имеет и формула для скорости сдвиговой деформации в теле Максвелла:

(d_i/dt)_M = (d/dt)_H  + (d/dt)_N,

где (d/dt)_H, (d/dt)_N - скорость сдвига в телах Гука и Ньютона.

Рис. 11. Модели тела Максвелла (а) и тела Пойнтинга–Томсона (б)

Подставляя в выражение для скорости сдвиговой деформации тела Максвелла значения скоростей деформаций тел Гука (d/dt = d/dt/ G) и Ньютона (см. первое уравнение в (8)), получим дифференциальное реологическое уравнение тела Максвелла:

 + Т dτ/dt =  d/dt (9)

где T = /G – время релаксации, dim T = с. Время релаксации T является важным реологическим параметром.

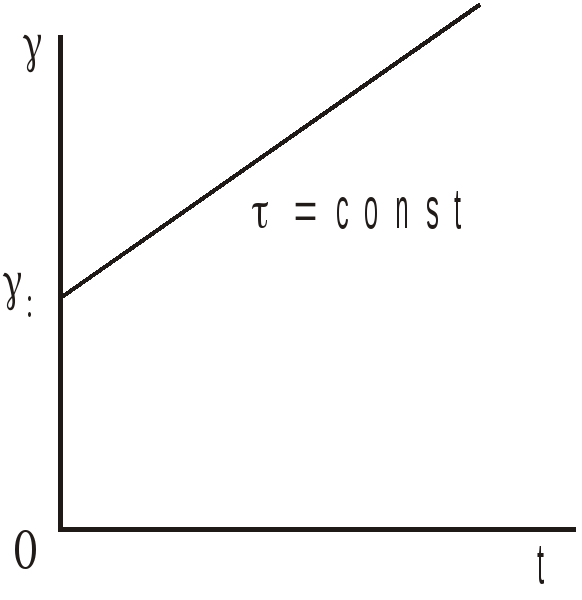
При постоянном напряжении dτ/dt = 0  и тело Максвелла превращается в тело Ньютона, т.е. тело ведет себя как вязкая жидкость. Рост деформации в теле Максвелла с течением времени t происходит по линейному закону

 = t/ + _о,

Рис. 12. Развитие деформации ползучести в теле Максвелла

где _о – величина деформации в момент времени t = 0. Этот процесс называется ползучестью (рис. 12).

При постоянной деформации ( = const) решение уравнения (9) имеет следующий вид:

 =_оe^–t/T ,

где _о есть начальное напряжение сдвига, t – время действия нагрузки.

Рис. 13. Релаксация напряжений в теле Максвелла

В соответствии с последним уравнением напряжение в теле Максвелла релаксирует (уменьшаются) практически до нуля (рис. 13).

Скорость развития релаксации напряжений определяется величиной времени релаксации: чем меньше Т, тем в большей степени материал проявляет жидкостные свойства и наоборот, чем больше Т, тем более твердообразным является материал.

Тело Максвелла следует рассматривать, как упруговязкое тело (вязкая жидкость, обладающая упругими свойствами). Проявление твердообразных и вязких свойств тела Максвелла зависит от соотношения времени t действия нагрузки и времени релаксации: если t << T, то в теле возникает, главным образом, упругая деформация и тело ведет себя как тело Гука. Если же справедливо неравенство t >> T, то в теле в большей степени проявляются свойства ньютоновской жидкости и доминирует вязкая деформация.

3.2.3. Тело Пойнтинга–Томсона: РТ = М│H₁ (рис.11 б). Структурная формула тела показывает, что в отличие от тела Максвелла в данном случае существует предел деформации, который определяется пружиной H_1.