2.4. Геометрическая интерпретация напряженного состояния

Прежде всего дадим геометрическую интерпретацию напряженного состояния изотропного тела, отобразив это состояние в трехмерном пространстве главных нормальных напряжений ₁, ₂, ₃ (рис. 4).

Начало координат соответствует отсутствию напряжений в теле. На осях координат лежат точки, отображающие простое растяжение или сжатие вдоль этих осей. На координатных плоскостях ₁₂,₂₃, ₁₃ расположены точки, отображающие плоское напряженное состояние.  

Прямая, наклоненная под одинаковыми углами  (cos  = 3^-0,5) ко всем трем координатным осям, называется пространственной диагональю или гидростатической осью. Она определяет положение точек, соответствующих гидростатическому состоянию:

₁ = ₂ = ₃ = P.

Единичный вектор h, направленный вдоль гидростатической оси, определяется выражением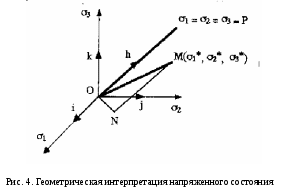

h = (i + j + k),

где i, j, k – единичные вектора по направлению осей ₁, ₂, ₃ (рис. 4). Плоскость, проходящая через начало координат (т.О) и перпендикулярная вектору h, называется девиаторной плоскостью.

Так как направление нормали к девиаторной плоскости задается проекциями вектора h на оси координат, то из общего уравнения плоскости, проходящей через рассматриваемую точку с координатами (₁^*, ₂^*, ₃^*),

A(₁ – ₁^*) + B(₂ – ₂^*) + C(₃ – ₃^*) = 0,

где A = i, B = j, C = k, следует, что уравнение такой плоскости имеет вид

₁ + ₂ + ₃ = 0.

Любая точка M трехмерного пространства ₁, ₂, ₃, имеющая координаты ₁^*, ₂^*, ₃^*, изображает некоторое напряженное состояние, характеризуемое главными напряжениями ₁, ₂, ₃ (Рис. 4).

Дадим геометрическую интерпретацию величинам _ср и _i. В качестве образа напряженного состояния мы будем рассматривать не точку М, а вектор ОМ, соединяющий начало координат О с точкой М(₁, ₂, ₃):

ОМ = _^*i + ₂^* j + ₃^* k.

Если мы разложим вектор OM, характеризующий напряженное состояние, на составляющие MN и ON, параллельную и перпендикулярную гидростатической оси, соответственно, то составляющая MN определится выражением MN = (OM ^h)h , где

OM·h = (₁^*i + ₂^*j + ₃^*k)·(i + j + k) =

= (₁^* + ₂^* + ₃^*)/  = _ср.

Следовательно

MN = _срh = _ср(i + j + k),

т.е. проекция вектора напряжений OM на гидростатическую ось пропорциональна величине среднего напряжения _ср.

Учитывая выражения для векторов MN и OM, можно записать

ON = OM – MN = (₁^*i + ₂^*j + ₃^*k) – _ср(i + j + k) =

= (₁ – _ср)i + (₂ – _ср)j + (₃ – _ср) k.

В последнем выражении величины, находящиеся в круглых скобках, представляют собой главные нормальные девиаторные напряжения

s₁ = (₁  – _ср), s₂ = (₂ – _ср), s₃ = (₃  – _ср).

Так как вектор ON по определению перпендикулярен гидростатической оси, то он должен лежать в девиаторной плоскости. Иначе говоря, проекции вектора напряжений OM (₁^*, ₂^*, ₃^*) на девиаторную плоскость равна «вектору девиаторных напряжений» s₁ , s₂ , s₃. Иначе это можно выразить и так: точка N  – проекция точки M на девиаторную плоскость  – изображает девиаторные напряжения, отвечающие точ-ке M. Любой вектор, принадлежащий девиаторной плоскости, характеризует девиатор напряжений какого-либо напряженного состояния M(₁^*, ₂^*, ₃^*).

Радиальное расстояние между любой точкой, находящейся на гидростатической оси, и точкой M, расположенной на плоскости, параллельной девиаторной плоскости (в частности, расстояние между точкой O (начало координат) и точкой N, расположенной на девиаторной плоскости, проходящей через начало координат), найдем по известной (раздел курса математики «Аналитическая геометрия в пространстве») формуле

ON = ·[(₁^* – ₂^*)² + (₂^* – ₃^*)² + (₁^* – ₃^*)²] / 6 ]^0.5 = 2^0.5·_i.

Иначе говоря, радиальное расстояние от гидростатической оси линейно зависит от интенсивности касательных напряжений _i.

Появление вектора ON связано с неравнокомпонентностью напряженного состояния. Совершенно очевидно, что когда рассматриваемая точка M находится на гидростатической оси, то вектор главных девиаторных напряжений ON отсутствует в силу того, что s₁ = 0, s₂ = 0, s₃ = 0.

Так как увеличение радиального расстояния ON означает увеличение интенсивности касательных напряжений _i , то для каждой точки M вектор ON определяет величину девиаторного напряжения, которое вызывает появление сдвигов, т.е. вектор ON определяет условие текучести для данного напряженного состояния.

Так как точка N является проекцией на девиаторную плоскость и любой другой точки, лежащей на прямой MN, то вектор главных нормальных девиаторных напряжений ON = s₁i + s₂j + s₃k является общим для всех точек любой прямой, перпендикулярной девиаторной плоскости. По этой причине если условие текучести выполняется для точки N , то оно будет выполняться и для всех точек бесконечной прямой NM. Все комбинации s₁, s₂, s₃, для которых выполняется данное условие текучести, образуют на девиаторной плоскости кривую текучести. Кривая текучести в девиаторной плоскости является направляющей цилиндра, образующие которого параллельны гидростатической оси. В пространстве главных нормальных напряжений возникает цилиндр текучести.