ФТЯР ЛЕКЦИИ

31

где R2=R+T.

По аналогии с ЯР в форме пластины докажем, что условие (16) является условием критичности, т.е. если уберем отражатель, условие (16) должно прей-

Пусть нет отражателя (Т=0). Тогда знаменатель в правой части (16) обращается в 0, а сама правая часть стремится к бесконечности. Тогда

J1( r R) J0( r R)

Т.к. функция J1( r R) ограничена при всех х, то указанное условие будет выполняться только при J0( r R) 0 или r R 2,405 (первый корень функции

Бесселя первого рода нулевого порядка) r 2,405R , что и требовалось доказать.

Как и в случае плоского ЯР введем понятие эффективной добавки за счет отражателя δ = R0 – R, где R0 – критический радиус цилиндрического ЯР без отражателя. Выразим R и подставим в левую часть условия критичности (16):

Рассмотрим ЯР, имеющий большие размеры, т.е. радиус велик по сравнению с величиной эффективной добавки δ << R. Тогда разложим (17) в ряд Тейлора по малому параметру r , ограничившись первым числом разложения (достаточно сложные математические выкладки опустим).

этом случае для правой части условия (16) воспользуемся асимптотическим раз-

В итоге сопоставляя (17) и (18), для больших ЯР получим условие критичности:

Это выражение с точностью до первых членов разложений совпадает с результатом, полученным для плоского ЯР. Надо заметить, что с уменьшением R необходимо учитывать больше членов разложения вследствие увеличения кривизны поверхности и полученное для δ выражение усложнится. Далее необходимо провести анализ δ при различных толщинах отражателя.

Таким образом, используя рассмотренный алгоритм решения подобных задач, можно решить в одногрупповом приближении задачи о сферическом ЯР с отражателем и о цилиндрическом ЯР с торцевым отражателем.

В заключении необходимо отметить, что все основные соотношения получены в предположении больших размеров ЯР. С уменьшением размеров ЯР точность одногруппового метода падает, т.к. большую роль начинают играть члены, следующие за первым членом разложения в ряды, и их надо учитывать, что приводит к получению сложных выражений.

2.6. Эффективные размеры активной зоны ЯР с отражателем. Эквивалентный ЯР

Размеры активной зоны, определенные с учетом эффективной добавки, называются эффективными размерами АЗ. Например, для реактора в форме бесконечной пластины эффективные размера АЗ составляют: Hэф = H +2δ. Так

33

как при эффективных размерах АЗ является критичной, то проводя критический анализ, можно воспользоваться расчетной моделью – эквивалентным ЯР. Эквивалентный ЯР – это реактор, имеющий эффективные размеры. Использование этой модели позволяет перейти при анализе АЗ от ЯР с отражателем к ЯР без отражателя. При этом для такого ЯР будет выполняться условие критичности реактора без отражателя (равенство материального и геометрического параметров) при условии использования в геометрическом параметре не геометрических, а эффективных размеров АЗ. Например, для цилиндрической АЗ в ЯР с отражателем с размерами H и R эффективные размеры равны:

Hэф = H + 2δ; Rэф = R + δ,

геометрический параметр определится зависимостью:

а эффективный коэффициент размножения – известным выражением:

kэф k exp(2 B22 ) . (1 B L )

Такой подход значительно облегчает решение задач и будет использоваться в дальнейшем (например, курсовой проект).

Так как в эквивалентном ЯР потоки нейтронов на границе должны обращаться в нуль, то становится ясен физический смысл эффективной добавки. Это расстояние, отсчитываемое от границы АЗ в отражатель, на котором аналитическое продолжение распределения потока нейтронов в АЗ реактора с отражателем обращается в нуль. Однако такое определение справедливо лишь в случае одногруппового приближения, когда влияние отражателя (наличие переходных областей) не учитывается. В общем случае, когда идет учет влияния отражателя, эффективная добавка более строго будет иметь физический смысл: это расстояние, отсчитываемое от границы АЗ в отражатель, на котором аналитическое продолжение асимптотического распределения потока нейтронов обращается в нуль.

34

Сферический ЯР с отражателем Рассмотрим сферический ЯР, состоящий из АЗ радиу-

сом R, окруженной отражателем толщиной Т.

Т R Порядок определения потоков нейтронов в АЗ и в отражателе остается тот же, что и в предыдущих случаях. Записывается уравнение ЯР отдельно для отражателя и

АЗ.

ля, положив Т=0. В этом случае правая часть (1) стремится к бесконечности и ; (геометрический параметр сферического ЯР

без отражателя).

Если рассмотреть условие (2), то при. Снова получена реальная картина ЯР без отражателя.

35

Проведем преобразования выражения (2), разделив обе части на: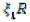

Вынесем в правой части за скобку: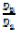

Приведем полученное выражение к удобному для анализа виду, вынеся в правой части за скобку:

(3)

Отсюда в общем случае:

Положим, что D1=D2, тогда:

Ве

рнемся к выражению (3) и проанализируем его для большого ЯР.

Разлагая левую часть (3) в ряд вследствие малости 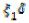ограничиваемся одним членом разложения ():

Для больших ЯР , тогда:

36

Используя условия (*) имеем, что второе слагаемое правой части стремится к нулю, отсюда:

Т.о. для больших сферических ЯР условие критичности совпадает с теми, что были получены ранее. (Анализ этих условий провести самостоятельно, аналогично плоскому ЯР).

34

3. МЕТОД МНОГИХ ГРУПП

До настоящего времени при решении задач физики ЯР нами использовался одногрупповой метод. При этом считалось, что в ЯР только тепловые нейтроны определяют все процессы, происходящие в нем: поглощение, деление ядер и др. В то же время считалось, что рожденные нейтроны надтепловых энергий не оказывают влияние на работу ЯР и служат лишь источником тепловых.

Однако анализ полученных в этом приближении результатов показывает, что большое количество допущений и приближений позволяют использовать такой подход в качестве самого первого (оценочного) приближения, например, одногрупповой метод позволяет получить неплохие результаты для гомогенных ЯР без отражателя (нереальный случай), имеющих большие размеры. С уменьшением размера АЗ точность этих результатов значительно падает. В то же время введение отражателя значительно ухудшает точность результатов метода даже для больших ЯР и аналитическое решение задач о критических размерах возможно в ограниченном числе случаев. Однако даже, когда аналитическое решение имеет место, одногупповой метод дает большие неточности. Например, распределение потока тепловых нейтронов в цилиндрическом ЯР с боковым отражателем в рамках одногруппового приближения является гладкой зависимостью, измерения фиксируют всплеск в этом распределении в отражателе.

Таким образом, одногрупповой метод может быть использован как базовый для более точных расчетов.

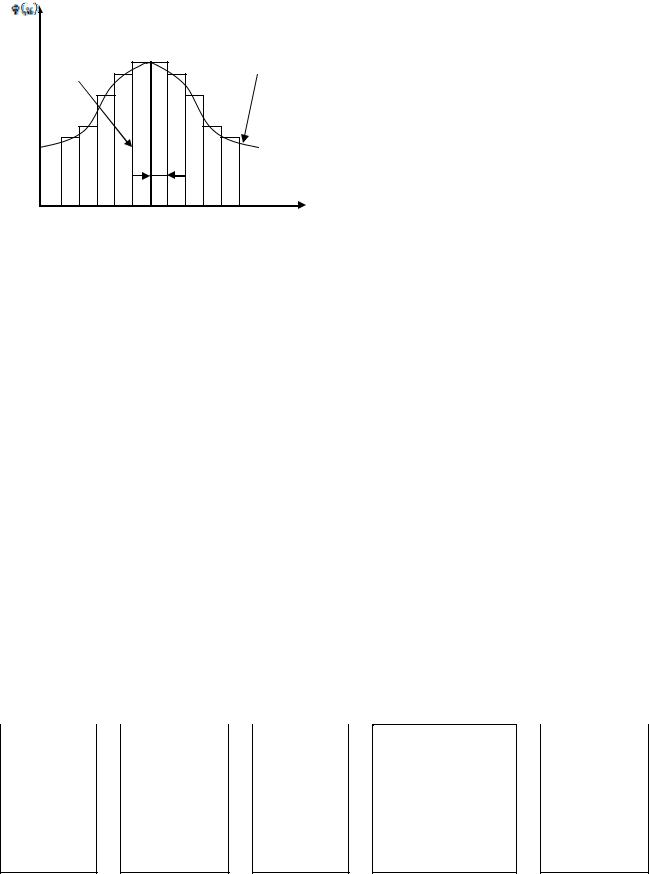
Основная причина такого положения вещей кроется в том, что не учтен тот факт, что на процессы в ЯР влияет не только поведение тепловых нейтронов, но и нейтронов других энергий. На рисунке представлен энергетический спектр нейтронов ЯР на тепловых нейтронах.

35

Видно, что условно можно выделить 3 основных составляющих спектра нейтронов:

быстрые нейтроны – нейтроны деления;

промежуточные (резонансные) нейтроны – замедляющиеся нейтроны;

тепловые нейтроны.

Также видно, что, несмотря на то, что количество тепловых нейтронов достаточно велико, потоки нейтронов других энергий тоже значительны, и они

не могут не влиять на процессы в ЯР.

Напомним, что спектр нейтронов деления описывается чаще всего уравне-

нием Уатта: n(E) C exp( E)sh 2E , где n(E) – доля нейтронов, имеющих энергию Е; C – константа, характеризующая тип делящегося нуклида (например, для U235 С ≈ 0,48). Основные характеристики этого спектра: средняя энергия E 2МэВ; наиболее вероятная энергия Ев 0,7 МэВ. Условно границей быстрой области считается энергия порядка 1 10 кэВ.

Взаимодействуя с ядрами среды, нейтроны замедляются и становятся резонансными, и спектр Уатта переходит в спектр Ферми, для которого

Ф(E) ~ E1 . Однако для этих энергий в энергетических зависимостях сечений

(особенно тяжелых ядер) наблюдаются резонансы. Поэтому спектр Ферми представляет собой не чистую зависимость E1 , а он осложнен резонансной

структурой особенно в области, прилегающей к тепловой группе, где наиболее ярко выражено резонансное поведение зависимости сечений от энергии.

Энергетическое распределение тепловых нейтронов описывается спектром Максвелла. Согласно классическому (для теплового движения атомов и молекул

36

среды) Максвелловскому распределению Ф(E) ~ exp( E) E . Это распределе-

ние имеет следующие характеристики: средняя энергия E 32 kT ; наиболее ве-

роятная энергия Ев kT, где T – температура среды, k – постоянная Больцмана. Однако в реальных конечных размножающих средах существует вероятность того, что тепловой нейтрон будет либо поглощен, либо испытает утечку. Вследствие этого время жизни теплового нейтрона конечно и полное тепловое равновесие с ядрами среды не устанавливается. В результате спектр тепловых нейтронов по форме и положению максимума сдвинут относительно классического спектра Максвелла в область более высоких энергий, т.е. средняя и наиболее вероятная энергия спектра тепловых нейтронов имеют более высокие значения, чем аналогичные характеристики классического спектра Максвелла для теплового движения ядер среды. Чем сильнее поглощение, тем более силен сдвиг в распределении Максвелла. Поэтому расчеты сечений в тепловой области при использовании параметров классического спектра Максвелла неточны. Поэтому для тепловых нейтронов принимают приближение: считается, что тепловые нейтроны распределены по спектру Максвелла, но при температуре нейтронного газа – температуре, определенной для нейтронов с учетом их поглощения и утечки. В связи с этим в рассмотрение вводят понятие стандартизированного теплового нейтрона Ест= kT при Т=20,40С Ест =0,0253эВ (Vст=2200м/с). Для этой энергии определяют сечения, которые в зависимости от решаемой задачи либо принимаются за сечения всей тепловой группы, либо яв-

ляется основой для усреднения сечений.

3.1. Сущность метода многих групп

Деление реакторного спектра на составляющие является условным. Кроме того, внутри каждой энергетической области вследствие ее достаточно больших интервалов поведение нейтронов очень различно и зависимости Ф(r, Е) очень сложны, что приводит к практической невозможности нахождения реальных распределений потоков нейтронов (и значит и критических параметров ЯР), т.к. в этом случае переменные r и E не разделяются.

Многогрупповое уравнение является исходным соотношением для расчета распределения нейтронов в ЯР в рамках метода многих групп. Его получение основано на составление баланса нейтронов, находящихся в точке с координатами r и имеющих энергию Е, т.е. рассматриваются нейтроны в состоянии (r,Е).

Составим такой баланс сначала на качественном уровне.

Реализуем записанный баланс в рамках диффузионного приближения для стационарного случая (левая часть баланса равна нулю):