
ФТЯР ЛЕКЦИИ
.pdf
87
нейтрон поглотился в топливе, он, во-первых, сначала должен поглотиться в топливном блоке в целом и, во-вторых, в самом топливе. Таким образом, коэффициент использования тепловых нейтронов можно представить как суперпозицию двух вероятностей Θ=Θ1Θ2, где Θ1 - вероятность для нейтрона поглотиться в топливном блоке, а Θ2 – вероятность для нейтрона поглотиться в самом топливе.
|
Труба |
Применим рассмотренный подход к определе- |
|
нию Θ в ячейках сложных решеток. Рассмотрим |
|
|
ТВЭЛ |
|
|
т/н |
сложную решетку, в которой расположение техноло- |
|
Зам-ль |
|
|
|
|
|
Границаячейки гических каналов соответствует разреженному типу |
|
|
|
решеток. Выделит элементарную ячейку такой решетки. |
|
|
|
|
|
Преобразуем реальную ячейку в эквивалентную следую- |
Rф |
щим образом. Ячейку в целом преобразуем уже известным |
|
|
|
способом, заменяя квадратную форму круговой, а вместо |
Rяч |
ТК зададим так называемый фиктивный цилиндрический |
|
блок. Радиус этого блока зададим равным внешнему радиусу трубы ТК, а сам фиктивный блок образуется путем гомогенизации всего содержимого ТК – горючего, оболочек ТВЭЛ, т/н, трубы ТК и др. Таким образом, реальную ячейку заменяем расчетной моделью, представляющей собой простую ячейку. Тогда согласно рассмотренному подходу коэффициент Θ можно представить следующим образом: Θ=Θ0Θф, где Θ0 - коэффициент использования тепловых нейтронов внутри фиктивного
блока; Θф - коэффициент использования тепловых нейтронов, поглощаемых в фиктивном блоке в целом, играющем в расчетной модели роль топливного блока.
Так как содержимое ТК гомогенизировано в фиктивный блок, то определение Θ0 расчет производится аналогично случаю гомогенной среды:
|
|
|
Rтоп |
топ |
|
|
0 |
|
a |
a |
|
aтоп aт/н aтр оболa |
|
||||
|
|
Raф |
|
||
|
|
|
где Raтоп - скорость поглощения тепловых нейтронов ядрами топлива; Raф - скорость поглощения тепловых нейтронов всеми материалами гомогенного фик-

88
тивного блока; топa ; тa /н; трa ; оболa ; - сечения поглощения топлива, т/н, материала трубы ТК, оболочки ТВЭЛ и др.
На втором этапе рассматриваем ячейку в целом, считая фиктивный блок аналогом блока горючего. В этом случае решается задача о коэффициенте Θ в двузонной ячейке либо с источником тепловых нейтронов в одной зоне (замедлителе), либо с источником тепловых нейтронов в двух зонах (замедлителе и фиктивном блоке).
Если теплоносителем является жидкий металл или газ, то можно пренебречь замедлением быстрых и, соответственно, рождением тепловых нейтронов в фиктивном блоке. Тогда определение Θф проводится по схеме простой ячейки
систочником тепловых нейтронов в зоне замедлителя:
1 1 a1V1 F (E 1)
ф a0V0
Если теплоносителем является легкая или тяжелая вода, то определение Θф проводится по схеме простой ячейки с источником тепловых нейтронов в зонах
замедлителя и фиктивного блока: |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a1V1 |
|
|
|
|
||
|
|
|
|
|
|
q0V0 |
|
|
|
|
|
|
|||||
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
F (E 1) |
|
|||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
q1V1 |
|
|
a0V0 |
|
|
||||||||
|
ф |
|
q V |
|
|
|
|
|
|
|
V |
|
|
||||
|
|
|
1 |
|
0 0 |
1 |
(F |
1) |
|
|
a1 1 |
(E 1) |
|
||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
q V |
|
|
|
|
|
|
|
V |
|
|||
|
|
|
|
|
1 1 |
|
|
|
|
|
|
a0 0 |
|
|
|||
На третьем этапе окончательно рассчитывают коэффициент использования тепловых нейтронов: Θ=Θ0Θф.
В заключении необходимо снова отметить, что расчеты ячейки на основе диффузионных уравнений являются недостаточно точными. Особенно эти неточности характерны для блоков топлива – источников сильного поглощения тепловых нейтронов. Однако для инженерных расчетов тепловых аппаратов такой подход приемлем. При расчете новых ЯР или нетипичных ячеек традиционных ЯР необходимо пользоваться более точными методами, основанными на различных методах решения кинетического уравнения.
5.4 Вероятность избежать резонансного захвата
89
В формуле 4-х сомножителей процесс резонансного поглощения учитывается коэффициентом φ. Причем учитывается только резонансное поглощение в U238, хотя в действительности происходит и в других изотопах горючего и других материалов, однако U238 обладает наиболее богатой резонансной структурой. Всю энергию замедляющихся нейтронов можно условно разделить на две группы: более высокоэнергетичная область, где относительно небольшие резонансы, расположенные близко друг к другу, частично перекрываясь; и область низких резонансных энергий, которая характеризуется сильными перекрывающимися уровнями и примыкает к тепловой области. Например, для U238 наиболее сильные резонансные уровни: 6,67; 20,9; 36,8; 66 эВ. Поэтому наиболее сильно резонансное поглощение именно во второй области. Следовательно, и гетерогенные эффекты в процессе резонансного поглощения наиболее присущи нейтронам надтепловых энергий.
Для гомогенной среды коэффициент φ равен:
|
N0 |
E f |
|
dE |
|
|
(E) exp Ra exp |
|
( a0 )эф |
(1) |
|||
s |
|
|||||
|
E |
|
E |
|||
|
|
|
|
|
|
|
где Ra – скорость поглощения резонансных нейтронов; N0 – ядерная концентрация резонансного поглотителя (топлива); s - замедляющая способность среды; Ef -
|
|
|
|
|
E f |
( a0 )эф |
dE |
Iэф – эффективный |
максимальная энергия нейтронов источника; |
||||||||
|
|
|
|
|
E |
|
E |
|
резонансный интеграл; ( a0 )эф a0 |
|
|
s |
|
– |
эффективное сечение поглощения; |
||
|
|
|
|
|||||
|
s |
a |
|
|
|
|||
|
|
|
|
|
|
|||
a0 – микроскопическое сечение поглощения резонансного поглотителя (топлива). Запишем выражение для эффективного сечения поглощения в следующем
виде (разделив числитель и знаменатель дроби на Σs):
( |
|
) |
|
|
|
|
|
s |
|
|
|
a0 |
|
|
|
a0 |
эф |
a0 |
|
|
|
|
|
N |
|
||||||
|
|
|
s |
a |
1 |
|
a0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
и проанализируем.
90
Если количество поглотителя будет расти N0→∞, то эффективное сечение поглощения уменьшается, и эффективный резонансный интеграл тоже уменьшается. Своего минимального значения эффективный резонансный интеграл достигнет в случае чистого резонансного поглотителя (урана). Этот эффект называется энергетической экранировкой или экранировкой резонансных уровней. Другими словами, высокие концентрации поглотителя приводят к тому, что спектр замедляющихся нейтронов «выедается», и поглотитель как бы сам себе мешает эффективно поглощать резонансные нейтроны.
С другой стороны при бесконечном разбавлении топлива замедлителем N0→0 эффективное сечение поглощения стремится к микроскопическому сечению поглощения ( a0 )эф a0 , и эффективный резонансный интеграл перехо-
дит в истинный Ia∞. В этом случае резонансный интеграл максимален.
Однако величина концентрация резонансного поглотителя N0 входит также и в множитель перед резонансным интегралом в формуле (1) для φ. Поэтому в любом случае влияние N0 на φ имеет разные знаки. Например, для бесконечно разбавленной среды Iaэф→ Ia∞ - максимален, однако перед интегралом в (1) стоит N0→0, и показатель экспоненциально стремится к нулю, а сам φ стремится к 1. Наоборот при N0→∞ Iaэф - минимален, однако N0 в выражении (1) находится также и перед интегралом, тогда показатель экспоненты стремится к –∞, а сам φ→0. Это следует и из физических соображений: в бесконечно разбавляемой среде нейтроны замедляются, не встречая ядер резонансного поглотителя и наоборот. Таким образом для увеличения φ надо или увеличивать обогащение топлива (уменьшить количество U238, для 100% обогащения φ ≈1) или смешать горючее с большим количеством эффективного замедлителя.
Другим способом увеличить φ является переход к гетерогенным системам.
Вгетерогенной системе φ выше по двум причинам:
т.к. топливо выделено пространственно, то основная часть нейтронов претерпевает процесс замедления вдали от блока горючего, тем самым избегая резонансного захвата;

91
наличия пространственного блок-эффекта за счет наружных слоев топлива (не путать с энергетической блокировкой).
Даже в случае гомогенной среды точный расчет φ возможен только в некоторых частных случаях. В гетерогенной среде это еще более сложно, так как необходимо учитывать не только зависимость потока нейтронов не только от энергии, но и от координат. Таким образом, вероятность избежать резонансного захвата для гетерогенной среды будет определяться как:
|
1 |
|
|
N0V0 |
гет |
|
|||
(E) exp Ra exp |
|
|
dr aФ(E)dE |
exp |
|
|
|
Iaэф |
(2) |
V |
яч |
|
V |
яч |
|||||
|
|
|
|
s |
|
|
|
||
где Iaгетэф - эффективный резонансный интеграл в гетерогенной среде; V0 и Vяч -
объем топлива и ячейки, соответственно; N0 - ядерная концентрация топлива;s - средняя по ячейке замедляющая способность. Таким образом, определе-
ние φ в гетерогенной среде сводится к определению Iaгетэф .
Прямое определение Iaгетэф достаточно сложно. Тем не менее, эту величину можно определить из физических соображений. Iaгетэф зависит от степени разбав-
ления топлива (необходимо учесть энергетическую блокировку), а также от размеров (объема) и формы поверхности топливного блока (необходимо учитывать пространственный блок-эффект). В связи с этим советскими учеными И.Н. Гуревичем и Н.Я. Померанчуком в 1943г. была разработана теория, согласно которой Iaгетэф может быть представлен как суперпозиция двух слагаемых. Для простой
разреженной решетки было предложено рассматривать Iaгетэф следующим образом:
Iaгетэф A B |
S |
(3) |
|
M |
|||
|
|
где S и M – площадь поверхности и масса блока горючего. Коэффициенты А и В определяются параметрами резонансных уровней U238 и зависит от вида горючего. Первое слагаемое описывает пространственно неблокируемое резонансное поглощение, как в гомогенной среде (учет энергетической блокировки) и зависит лишь от степени разбавления среды замедлителем, т.е. от N0 горючего. Вто-

92
рое слагаемое описывает пространственный блок-эффект и площадью поверх-
ности и объемом (пропорциональным массе) блока топлива. |
|
|
||||||||||
|
Коэффициенты А и В определяются экспериментально для конкретной ре- |
|||||||||||
шетки. В результате были предложены следующие соотношения: |
|
|
||||||||||
|
разреженная |
|
решетка |
с блоками |
из металлического урана: |
|||||||
|
Iaгетэф 4,05 25,8 |
S |
(при |
0,07 |
S |
0 0,53); |
|
|
||||
|
M |
|
|
|
||||||||
|
|
|
|
|
|
M |
|
|
|
|||
|
разреженная |
решетка с |
блоками |
из UО2: Iaгетэф 5,55 26,6 |
S |
|
||||||
M |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
(при 0,08 |
S |
0 0,7). |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
M |
|
|
|
|
|
|
|
|
||
При работе с приведенными формулами необходимо иметь в виду, что если размерность MS - см2/г; то размерность Iaгетэф – барн.
В простых тесных решетках ТВЭЛы расположены настолько близко друг к другу, что спектр падающих на их поверхность резонансных нейтронов существенно зависит от присутствия соседних блоков (эффект затенения). Это приводит к заметному увеличению φ. Для учета этого факта при определении Iaгетэф
используется следующий подход: считается, что в тесных решетках блоки топлива захватывают резонансные нейтроны не всей своей поверхностью, а только ее частью. Такая часть поверхности топливного блока называется эффективной поверхностью, а ее площадь обозначается – Sэф. Тогда при определении Iaгетэф по соотношению (3) во второе слагаемое вводится дополнительный множитель – коэффициент затенения блоков p (поправка Петрова), который по определению
 , где Sэф – площадь эффективной поверхности ТВЭЛ, S - полная площадь поверхности ТВЭЛ. Таким образом, коэффициент затенения p учи-
, где Sэф – площадь эффективной поверхности ТВЭЛ, S - полная площадь поверхности ТВЭЛ. Таким образом, коэффициент затенения p учи-
тывает уменьшение «поглощающей» поверхности блока вследствие затенения одного блока другим. p определяется формой и размерами топливного блока.
Точный расчет p достаточно сложен. Поэтому разработано множество эмпи-

93
рических соотношений. Так, например, для цилиндрических ТВЭЛ может использоваться следующее эмпирическое соотношение:
|
|
p 1 |
|
|
exp( t t1l1) |
|
|
|
1 |
t1l1(1 t t) |
|||
|
|
|
||||
где t1 |
- полное макроскопическое сечение взаимодействия замедлителя; l1 - пара- |
|||||
метр l |
4V1 |
, V1 и S0 – объем замедлителя в ячейке и площадь поверхности |
||||
1 |
|
S0 |
|
|
|
|
|
|
|
|
|
|
|
ТВЭЛ, соответственно; t - кратчайшее расстояние между поверхностями блоков,
измеренное в единицах l1; t a d0 , а – шаг решетки (размер ячейки); d0 - диа- |
||||||||||||
|
|
1 |
l1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метр ТВЭЛ; t |
- поправка Боналуми t |
l1 t1 (7 l |
|
t1 |
); β - коэффициент формы |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ячейки: 17 |
3 |
– для шестигранной ячейки, 17 |
8 |
– для квадратной ячейки. |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, определение Iaгетэф |
в тесных решетках проводится с учетом |
|||||||||||
коэффициента затенения p : |
|
|
|
|
|
|
|
|
|
|
||
|
|
Iaгетэф A B |
|
S |
p |
(4) |
|
|
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
M |
|
|
|
|
|
|
|
В сложных решетках в технологическом канале находится несколько ТВЭЛ, которые также затеняют друг друга. По аналогии с тесными решетками можно ввести коэффициент затенения в технологическом канале - к , который
в этом случае также равен |
к |
Sэфк |
, где Sк |
- суммарная эффективная пло- |
|
S |
эф |
|
щадь всех ТВЭЛ в технологическом канале; S - суммарная полная площадь всех ТВЭЛ в технологическом канале.
Однако определение к значительно сложнее, чем p , т.к. ТВЭЛы в сборке находятся в неравных условиях: периферийные ТВЭЛ затеняются значительно меньше, чем центральные. Поэтому точный расчет к практически невозможен. В связи с этим применяют приближение, считая, что ТВЭЛ в технологическом канале находятся в равных условиях. После чего для каждого ТВЭЛ в зависимости от его местоположения определяют поправку Петрова p . Тогда находят к :
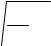
|
94 |
||
к |
|
|
- среднее значение коэффициента затенения для отдельных ТВЭЛ в |
p |
|||
технологическом канале. Таким образом, определение Iaгетэф в сложных решетках ведется по аналогии с простыми сложными решетками. При этом в происходит замена p на к :
Iaгетэф A B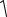 MS к
MS к
Надо заметить, что все рассуждения верны в том случае, когда отсутствует взаимное влияние технологических каналов друг на друга, что выполняется в большинстве случаев. Если каналы расположены близко, то учет из взаимного влияния необходим, и может быть проведен только численными методами.
5.5Коэффициент размножения на быстрых нейтронах
ВЯР на тепловых нейтронах основную роль играет деление под действием
тепловых нейтронов. Однако в гетерогенных ЯР нельзя пренебречь вкладом μ. Этот вклад впервые был оценен при создании ЯР на природном уране, когда расчеты без учета μ давали незначительное превышение kэф над единицей, однако реальность дала увеличение на несколько %.
При делении U235 возникают быстрые нейтроны с энергией от 0,5 до 15 МэВ (спектр Уатта). Средняя энергия – 2МэВ, наиболее вероятная – 0,7МэВ. Эти быстрые нейтроны с энергией выше порога деления U238 ( 1МэВ) могут вызвать его деление. Таким образом, в ЯР появляется некоторое дополнительно количество нейтронов.
Рассмотрим процессы, которые могут произойти с быстрыми нейронами в блоке топлива при взаимодействии с U238:
1.Деление. Сечение деления, усредненное по спектру деления, равно σf ≈0,31 б.
2.Упругое рассеяние. Т.к. ядро U238 тяжелое, то энергия нейтронов в этом взаимодействии практически не меняется, и он остается способным вновь вызвать деление U238. Среднее по спектру Уатта сечение упругого рассеяния на U238 σe ≈ 4,2 б.
3.Неупругое рассеяние. В результате энергия нейтрона становится ниже порога деления, и он не может вызвать деление U238. Среднее по спектру Уатта сечение неупругого рассеяния на U238 σe ≈ 2 б.
95
4. Радиационный захват U238. Среднее по спектру Уатта сечение радиационного захвата U238 σс ≈ 0,06 б.
Таким образом, среднее по спектру Уатта полное сечение взаимодействия быстрыхнейтроновсU238 составляетσс≈6,6б.Тежепроцессыхарактерныи дляU235.
Процесс деления на быстрых нейтронах происходит в то время, когда быстрый нейтрон, возникший при делении U235, в первый раз пересекает блок горючего. Вероятность для нейтрона, вылетевшего из блока, вернуться обратно с энергией выше порога деления пренебрежимо мала. Пренебрежем также вероятностью того, что быстрый нейтрон, рожденный в блоке горючего, вызовет деление в другом блоке, т.е. достигнет другого блока, не замедлившись. Иначе говоря, рассмотрим размножение на быстрых нейтронах в топливном блоке разреженной решетки из металлического урана. Будем считать, что топливо слабообгащенное и, следовательно, взаимодействием быстрых нейтронов с U235 пренебрегаем.
Быстрый нейтрон способен увеличить k∞, если он попадет в замедлитель, т.е. выйдет из блока, или снизит за счет неупругого рассеяния свою энергию внутри блока, тем самым, увеличивая свою ценность. Таким образом, коэффициент μ можно представить как суперпозицию количества нейтронов, вышедших из блока, приходящегося на один рожденный быстрый нейтрон (μ1), и количества нейтронов, неупруго рассеявшихся в блоке, приходящегося на один возникший быстрый нейтрон (μ2):
μ = μ1 + μ2
Надо заметить, что полученные результаты будут не справедливы в тесных решетках.
Обозначим через Р вероятность того, что родившийся какой-то точке r топливного блока быстрый нейтрон испытает в нем любое взаимодействие в точке r΄.
Определим μ1 – составляющую коэффициента μ, показывающую количество быстрых нейтронов, вышедших из блока.
Если быстрый нейтрон вызовет деление, то новые быстрые нейтроны тоже либо вызовут деление, либо вылетят из блока, либо неупруго рассеются, а новые нейтроны снова повторят судьбу, т.е. имеет место каскадный процесс.

96
Пусть произошло деление ядер, и родился быстрый нейтрон. Для него вероятность не испытать ни одного столкновения и, соответственно, выйти из блока составит 1–Р. При этом вероятность для этого нейтрона вызвать деление
составит и, как следствие, родить новые нейтроны, составит tf P . С другой
стороны, этот же нейтрон может упруго рассеется в топливе, не потеряв энергии, и остаться способным вызвать новое деление, оставаясь быстрым. Вероят-
ность такого процесса составит el P .
t
Таким образом, после первого взаимодействия в топливном блоке появится в
расчете на первичный быстрый нейтрон |
f |
P el P быстрых нейтронов. Из |
||||||||
|
t |
|||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
этих нейтронов часть снова вылетит из блока: |
|
|
P |
|
el |
|
P) – число |
|||
|
|
|||||||||
|
t |
t |
P (1 |
|||||||
|
|
|
|
|
|
|
|
|||
нейтронов, испытавших одно взаимодействие и вылетевших из блока.
По аналогии можно найти число нейтронов, испытавших два взаимодействия и
|
f |
|
|
|
|
|
2 |
|
||||
вылетевших из блока |
|
|
|
|
P |
|
|
el |
|
|
(1 P); испытавших три взаимодействия |
|
|
|
|
|
|
|
|||||||
|
t |
t |
P |
|||||||||
|
|
|
|
|
|
|
||||||
|
|
f |
|
|
|
|
|
3 |
||||
и вылетевших из блока |
|
|
|
P |
|
|
el |
|
(1 P) и т.д. |
|||
|
|
|
|
|||||||||
|
|
|
t |
P |
||||||||
|
|
t |
|
|
|
|
|
|
||||
Таким образом, часть коэффициента μ, отвечающая за нейтроны, вышедшие из блока, будет определяться следующим выражением:
|
f |
|
|
|
|
f |
|
|
|
2 |
|
||
1 |
|
|
P |
|
el |
|
|
|
P |
|
el |
|
(1 P) (1) |
|
|
|
|
||||||||||
(1 P) |
t |
t |
P (1 |
P) |
t |
t |
P |
||||||
|
|
|
|
|
|
|
|
||||||
Выражение (1) представляет геометрическую прогрессию, первый член которой
|
f |
|
|
|
|
|
|
a1 |
|
|
P |
|
el |
|
1. Тогда сумма членов этой про- |
|
|
||||||
= (1 –Р), а знаменатель q |
t |
t |
P |
||||
|
|
|
|
|
|||
грессии будет равна:
