
математика
.pdf
Задание № 16. Уравнение прямой, проходящей через точки А (5;-3) и В (2;4) имеет вид …
1) y = 7 х + 26 ;
33
2)y = − 7 х + 26 ;
33
3)y = − 3 х + 3 ;
726
4)y = −х + 2.
Задание № 17. Уравнение прямой, проходящей через точку М(2;–5) параллельно прямой 4x + y − 2 = 0 имеет вид …
1)4x + y − 3 = 0;
2)x − 4 y − 22 = 0;
3)4x − y − 3 = 0;
4)4x + y + 3 = 0.
Задание № 18. Каноническое уравнение эллипса с полуосями а=5 и b=3 имеет вид …
1) |
x2 |
+ |
y2 |
= 1; |
|
|
53
2)x2 + y2 = 0; 25 9
3)x2 + y2 = 1; 25 9
4)x2 − y2 = 1. 25 9
Задание № 19. Дано уравнение гиперболы (x +1)2 − y2 = 1 . Тогда расстояние ме-
3 4
жду её фокусами равно …
1)5;
2)10;
3)1;
4)6.
61
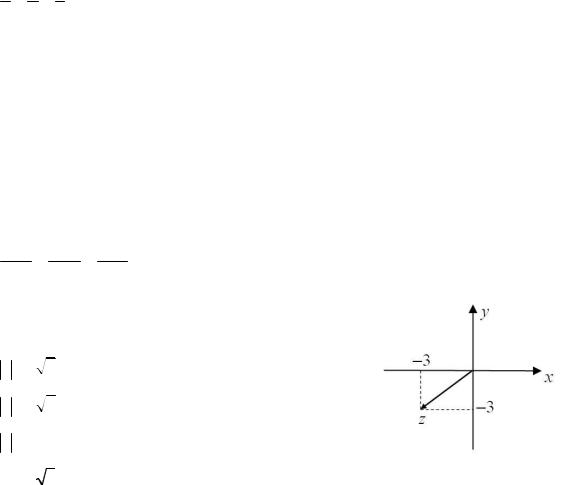
Задание № 20. Центр окружности x2 − 8x + y2 + 6 y + 21 = 0 находится в точке …
1)(-4;3);
2)(4;3);
3)(-4;-3);
4)(4;-3).
Задание № 21. Плоскость отсекает на координатных осях Ох, Оy и Oz отрезки длиной 3, 5 и 2 ед. соответственно. Тогда уравнение плоскости имеет вид …
1)3x + 5 y + 2z = 0;
2)10x + 6 y +15z − 30 = 0;
3)10x + 6 y +15z = 0;
4)x = y = z . 3 5 2
Задание № 22. Канонические уравнения прямой, проходящей через точки А(-5;3;8) и В(2;0;6), имеют вид …
1) |
x + 5 |
= |
|
y − 3 |
= |
z − 8 |
; |
||
−3 |
3 |
|
|||||||
|
|
|
14 |
|
|
||||
2) |
x − 5 |
= |
|
y + 3 |
= |
z + 8 |
; |
||
7 |
|
−3 |
−2 |
||||||
|
|
|
|
|
|
||||
3) |
x + 5 |
= |
y − 3 |
= |
z − 8 |
|
; |
||
|
−3 |
−2 |
|||||||
|
7 |
|
|
|
|
|
|||
4)x + 5 = y − 3 = z − 8 . 2 0 6
Задание № 23. На рисунке 44 изображено комплексное число. Тогда его модуль и аргумент равны …
1)z = 3
 2,ϕ = 135 ;
2,ϕ = 135 ;
2)z = 3
 2,ϕ = −135 ;
2,ϕ = −135 ;
3)z = 18,ϕ = −135 ;
|
|
= 3 |
|
|
|
4) |
z |
2,ϕ = 45 . |
Рисунок 44 |
||
Задание № 24. Значение выражения (5 − 2i)(i +1) − 3i7 |
равно … |
||||
1)7 + 6i ;
2)3 + 6i ;
3)7 ;
4)3 + 3i .
62
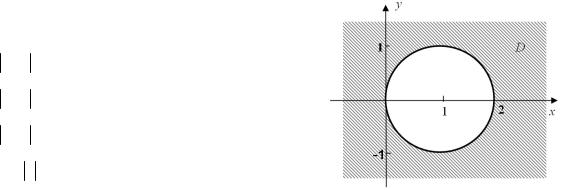
Задание № 25. Все точки комплексной плоскости z=x+yi, принадлежащие множеству D, изображённому на рисунке 45,
удовлетворяют условию …
1)z -1 ³1;
2)z -1 >1;
3)z +1 ³1;
4)0 £ z £ 2.
Рисунок 45
Тест 2
Задание № 1. Укажите соответствие между определителем и результатом его вычисления …
|
|
5 |
|
-2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1) |
|
0 |
|
1 |
|
|
2 |
|
; |
|
|
|
|
|
1) |
-5; |
|
|
|
|
|
|
|||
|
|
-6 |
|
3 |
|
|
1 |
|
|
|
|
|
|
|
2) |
10; |
|
|
|
|
|
|
|||
|
|
6 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
3) |
-7; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) |
|
0 |
2 |
1 |
|
; |
|
|
|
|
|
|
|
|
4) |
17; |
|
|
|
|
|
|
|||
|
|
3 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
5) |
4; |
|
|
|
|
|
|
|||
3) |
|
7 |
-1 |
|
; |
|
|
|
|
|
|
|
|
|
|
6) |
-3. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4) |
|
-5 |
|
0 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание № 2. |
Положительный корень уравнения |
|
0 |
-1 |
x |
|
= 0 равен ___. |
||||||||||||||||||
|
|
||||||||||||||||||||||||
|
1 |
1 |
5 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
x |
2 |
|
|
Задание № 3. |
Пусть ( x0 ; y0 ) |
– |
решение |
системы |
линейных уравнений |
||||||||||||||||||||
5x - y = 3, |
|
|
|
|
Тогда 2x0 - y0 равно ___. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4x + 3y = 10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
-2 |
3 |
|
|
|
|
|
|
|
|
|
Задание № 4. |
Дана матрица |
|
1 |
0 |
4 |
|
. Если А– В=Е, то матрица В равна |
||||||||||||||||||
А = |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
5 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
…
63

|
1 |
−1 |
4 |
|
|
|
|
|
1) |
|
2 |
1 |
5 |
|
; |
|
|
|
|
|
|
|||||
|
|
8 |
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
−2 |
3 |
|
|
|
||
2) |
|
1 |
−1 |
4 |
|
; |
|
|
|
|
|
|
|||||
|
|
7 |
5 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
−4 |
2 |
|
−3 |
|
|||
3) |
|
−1 |
1 |
|
−4 |
|
; |
|
|
|
|
||||||
|
|
−7 |
−5 |
|
−1 |
|
|
|
|
|
|
|
|
||||
|
6 |
−1 |
4 |
|
|
|
|
|
4) |
|
2 |
1 |
5 |
|
|
|
|
|
. |
|
|
|||||
|
|
8 |
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|||
Задание № 5. Дана матрица |
−1 |
2 |
−7 |
. Тогда произведение АВ сущест- |
|
В = |
|
|
|
||
|
|
5 |
8 |
4 |
|
вует, если число столбцов матрицы А равно ____.
Задание № 6. |
Даны матрицы |
|
−1 |
2 |
|
и |
|
3 |
. Пусть матрица С=АВ. То- |
А = |
|
|
|
В = |
|
||||
|
|
|
2 |
6 |
|
|
|
−1 |
|
гда элемент с21 равен ___. |
|
|
|
|
|
|
|
|
|
Задание № 7. |
2 |
3k |
не имеет обратной матрицы при k, равном |
||||||
Матрица А = |
|
||||||||
|
1 |
6 |
|
|
|
|
|
|
|
___.
Задание № 8. Ранг матрицы А равен 3. Тогда ранг матрицы 2А равен ___. Задание № 9. На координатной плоскости изображён
вектор a (рисунок 46). Тогда его первая координата
равна ___. |
|
|
|
|
|
Задание № 10. Дано двумерное векторное пространство |
|||||
с базисом e |
, e . Если вектор |
e |
= (−3; 2) , то вектор |
e |
|
1 |
2 |
1 |
|
2 |
|
может иметь координаты … |
|
|
|
|
|
|
|
|
Рисунок 46 |
||
1)e2 = −1; 2 ;
3
2)e2 = (2;5) ;
3)e2 = (6; −4) ;
4)e2 = (3; −2) .
64
Задание № 11. Линейное пространство не образует множество …
1)квадратных матриц 2-го порядка;
2)натуральных чисел;
3)действительных чисел;
4)двумерных векторов.
Задание № 12. Укажите |
положительное значение k, при |
котором |
векторы |
||||||||||
a = (3; −k;1+ k ) |
и b = (−2; −4; k ) перпендикулярны. ____ |
|
|
|
|||||||||
Задание № 13. Линейный оператор переводит векторы x |
= (0; 2) и x |
= (−1;3) в |
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
векторы |
y = (−2;8) и |
y |
= (−5;9) |
соответственно. Тогда матрица линейного |
|||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
оператора имеет вид … |
|
|
|
|
|
|
|
|
|
||||
1) |
A = |
2 |
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
−1 |
4 |
|
|
|
|
|
|
|
|
|
|
2) |
A = |
0 |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
−1 |
3 |
|
|
|
|
|
|
|
|
|
|
3) |
A = |
2 |
−1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
4) |
A = |
−2 |
8 |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
−5 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−2 |
1 |
0 |
|
|
|
||
Задание № 14. Матрице |
|
|
1 |
0 |
4 |
|
|
|
|
||||
A = |
соответствует квадратичная форма |
||||||||||||
|
|
|
|
|
|
|
0 |
4 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1)L = −2x12 + x1 x2 + 4x2 x3 + 5x32 ;
2)L = −2x12 + 2x1 x2 + 8x2 x3 + 5x32 ;
3)L = 2x12 + 2x1 x2 + 8x2 x3 + 5x32 ;
4)L = −2x12 + x22 + 2x1 x2 + 8x2 x3 + 5x32 .
Задание № 15. Квадратичная форма x2 − 3xy + 3y2
1)является отрицательно определённой;
2)не является знакоопределённой;
3)является положительно определённой.
65
Задание № 16. Координаты точки С, симметричной точке А(-1;4) относительно точки В(2;5), равны …
1)(1;-4);
2)(5;6);
3)(0,5;4,5);
4)(1;7).
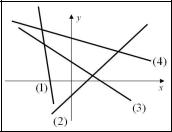
Задание № 17. Даны прямые (рисунок 47). Наименьший угловой коэффициент имеет прямая под номе-
ром _____.
Рисунок 47
Задание № 18. Дано уравнение прямой в параметрическом виде x = 3t − 4,
y = 6t + 5.
Тогда угловой коэффициент прямой равен ___.
Задание № 19. Точка М(3;-7) является основанием перпендикуляра, опущенного из начала координат на прямую. Тогда уравнение этой прямой имеет вид …
1)3x − 7 y = 0;
2)3x − 7 y − 58 = 0;
3)3x − 7 y + 58 = 0;
4)3x + 7 y − 58 = 0.
Задание № 20. Координаты центра окружности x2 + y2 + 6x − 7 = 0 равны …
1)(0;0);
2)(3;0);
3)(-3;0);
4)(0;-3).
Задание № 21. Дано уравнение параболы y2 = −12x . Тогда уравнение её дирек-
трисы имеет вид …
1)x=6;
2)x=3;
3)y=3;
4)y=-3.
66

Задание № 22. |
Точка А(−1;3; z ) принадлежит плоскости 5x + y − 2z + 4 = 0 . Тогда |
||||||||||||
z равно ___. |
|
|
|
|
|
|
|
|
|
|
|||
Задание № 23. |
Угол между прямыми |
x −1 |
= |
y |
= |
z + 4 |
и |
x |
= |
y − 4 |
= |
z + 2 |
равен |
|
−3 |
|
|
|
|
||||||||
|
5 |
|
0 |
3 |
5 |
0 |
|
||||||
___ (градусов).
Задание № 24. Число 2i24 − 3i7 − 3i равно ___.
Задание № 25. Комплексное число z = 2 − 2i в тригонометрической форме записи имеет вид …
|
|
|
|
π |
π |
|
|
|
1) |
z = 2 2 |
; |
||||||
cos |
|
+ sin |
|
|||||
|
|
|
|
4 |
4 |
|
|
|
2) 2) z = 2 |
|
|
− |
π |
|
− |
cos |
|
+ i sin |
||||
|
|
|
|
4 |
|
|
; 4
|
z = 2 |
|
|
|
− |
π |
+ i sin |
|
− |
π |
|
|||
3) |
2 |
; |
||||||||||||
cos |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
4) |
z = 2 |
|
|
π |
+ i sin |
π |
|
|
|
|
||||
2 |
|
|
|
|
||||||||||
cos |
|
|
. |
|
|
|
|
|||||||
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|
||
Тест 3 (Кейсы)
1.1 Предприятие производит продукцию 2-х видов – S 1 и S2, используя для этого сырьё двух типов – С1 и С2. В таблице приведены нормы затраты сырья на производство единицы продукции каждого вида и объёмы расхода за один день:
Нормы расхода сырья на ед. продукции, усл. ед. |
|
Вид сырья |
|
|
|
||
С1 |
С2 |
||
|
|||
|
|
|
|
Продукция S1 |
4 |
3 |
|
|
|
|
|
Продукция S2 |
5 |
2 |
|
|
|
|
|
Расход сырья на 1 день, усл. ед. |
1700 |
890 |
|
|
|
|
Пусть ежедневно предприятие выпускает х1 и х2 ед. продукции каждого вида соответственно. Тогда математическая модель ежедневного выпуска продукции каждого вида может иметь вид …
4x1 + 3x2 = 1700, 1) + =
5x1 2x2 890.
4x1 + 5x2 = 1700, 2) + =
3x1 2x2 890.
67
x + x |
|
= 7, |
3) 1 |
2 |
|
7x1 + 7x2 = 2590.
9x + 5x = 2590,
4)+ =
x1 x2 14.
1.2Для задачи 1.1 установите соответствие между видом продукции и ежедневным объёмом его выпуска:
1.Ежедневный объём выпуска продукции S1.
2.Ежедневный объём выпуска продукции S2.
1)150
2)705
3)104
4)220
1.3Для задачи 1.1 известна стоимость единицы сырья каждого типа: С=(8;12).1 2
Тогда стоимость сырья, затрачиваемого ежедневно на производство всей продукции 1-го вида, будет равна ….
2.1 Данные об исполнении бюджета за отчётный период приведены в таблице, в которой заданы коэффициенты прямых затрат и конечная продукция отраслей:
Отрасль |
|
Потребление |
Конечная |
|
|
|
|
||
№ 1 |
|
№ 2 |
продукция (у.е.) |
|
|
|
|||
|
|
|
||
|
|
|
|
|
№ 1 |
0,3 |
|
0,2 |
25 |
|
|
|
|
|
№ 2 |
0,2 |
|
0,1 |
271 |
|
|
|
|
|
Тогда матрица коэффициентов полных затрат имеет вид …
1 |
3 |
2 |
|
|
|
1) |
|
|
|
|
; |
|
|
||||
10 |
2 |
1 |
|
|
|
1 |
−1 |
2 |
|
|
||
2) |
|
|
|
−3 |
|
; |
|
|
|||||
1000 |
|
2 |
|
|
||
1 |
90 |
20 |
|
|
|
3) |
|
|
|
|
; |
|
|
||||
59 |
20 |
70 |
|
|
|
1 |
70 |
20 |
|
|
|
4) |
|
|
|
. |
|
|
|
||||
59 |
20 |
90 |
|
|
|
68

2.2 Для задачи 2.1 объём валовой продукции отрасли №1 равен ___.
3.1 Потребитель тратит весь свой доход на потребление двух благ А и В. В таблице приведены данные за три месяца об объёмах потребления и динамике изменения дохода потребителя по отношению к предыдущему месяцу:
Месяц |
Потребление |
Доход (у.е.) |
||
|
|
|||
Благо А (ед.) |
Благо В (ед.) |
|||
|
|
|||
|
|
|
|
|
1 |
25 |
5 |
|
|
|
|
|
|
|
2 |
30 |
7 |
увеличился на 25% |
|
|
|
|
|
|
3 |
32 |
10 |
увеличился на 16,8% |
|
|
|
|
|
|
Тогда отношение стоимости единицы блага А к стоимости единицы блага В равно …
1)3 ;
5
2)5 ;
3
3)1 ;
5
4)1 .
2
3.2Если стоимость единицы блага А равна 60 у.е., то доход потребителя в 3-м
месяце изменился на ____ у.е. (по отношению к предыдущему месяцу).
69
Приложение В
Глоссарий
Абсцисса – первая координата точки на плоскости или в пространстве. Обозначение: х.
Алгебраическая форма записи комплексного числа – запись комплексного
числа в виде z = x + yi, где x, y R, i = 
 −1 − мнимая единица.
−1 − мнимая единица.
Алгебраическое дополнение элемента определителя (или матрицы) aij – минор этого элемента, взятый со знаком (-1)i+j. Обозначение: Аij
Аналитическая геометрия – область математики, изучающая геометрические фигуры с помощью алгебраических методов. Основана на методе координат, впервые применённом Декартом.
Аппликата – третья координата точки в пространстве. Обозначение: z. Аргумент комплексного числа – угол между вектором, изображающим комплексное число на плоскости, и положительным направлением оси Ох. Обозначение: arg z. Рассматривают обычно главное значение аргумента, т.е. угол, расположенный в интервале (-π;π].
Асимптота графика функции – прямая, такая, что при неограниченном удалении от начала координат расстояние между графиком и прямой стремится к нулю, т.е. график неограниченно приближается к своей асимптоте, но не пересекает её.
Асимптоты гиперболы – диагонали прямоугольника гиперболы, к которым гипербола неограниченно приближается, но не пересекает.
Базис линейного n-мерного пространства – любая комбинация n линейно независимых векторов этого пространства. Любой вектор пространства можно единственным образом представить в виде линейной комбинации базисных векторов.
70
