
математика
.pdf
91.Найти площадь треугольника АВС, если известны координаты его вер-
шин: А(6;-3), В(-2;0), С(4;5).
92.Найти площадь четырёхугольника АВСD: А(-7;2), В(0;4), С(5;1), D(3;-6).
Задачи для самостоятельной работы
93.В треугольнике АВС найти длину стороны ВС и длину медианы ВМ, если А(-8;3), В(-2;6), С(6;5).
94.На биссектрисе 1-го координатного угла найти точку, отстоящую от точки М(5;3) на расстоянии 
 10 .
10 .
95.Найти координаты точки пересечения медиан треугольника АВС: А(-1;7),
В(3;11), С(6;12).
96.Известно, что точка С(-4;8) делит отрезок АВ в соотношении 2:5. Найти координаты точки В, если А(-7;10).
97.Вычислить площадь треугольника АВС: А(3;8), В(5;-6), С(10;4).
4.2. Полярные координаты
ρ, φ – полярные координаты (рисунок 7). ρ – полярный радиус (длина отрезка ОМ),
ρ≥0.
φ – полярный угол, φ (-π;π].
Рисунок 7
Связь между полярными и прямоугольными координатами
Переход от полярных к прямоугольным
координатам: x = ρ cosϕ
y = ρ sin ϕ
Рисунок 8
31

|
|
ρ = |
|
x2 + y2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
− для 1,4 - й четвертей |
||||||
|
|
|
arctg |
|
||||||||
|
|
x |
||||||||||
От прямоугольных к полярным: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
ϕ = |
180 |
+ arctg |
y |
− для 2 − й четверти |
||||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
−180 |
|
+ arctg |
|
− для 3 − й четверти |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
ЗАДАЧИ |
|
|
|
|
|
|
|
|
|||
Для аудиторной работы |
|
|||||||||||
98. Найти прямоугольные координаты точек А(6; π ), В(2; 3π ), С(3; 6π ).
2 4 5
99. Найти полярные координаты точек, симметричных относительно поляр-
ной оси точкам А(3; π ), В(4; − 2π ).
|
|
3 |
3 |
100. |
Найти полярные координаты точек, симметричных относительно полю- |
||
са точкам А(1; π ), В(5; − π ). |
|||
|
4 |
|
3 |
101. |
Построить линии, заданные уравнениями: |
||
а) |
ρ = 4 б)ϕ = − π |
в) |
ρ = 4 sin ϕ г) ρ = 2ϕ д) ρ = 1+ cosϕ |
|
3 |
|
|
102.В полярной системе координат написать уравнение окружности, центр которой находится в точке А(3;π ), и радиус равен 3.
103.Даны точки в полярной системе координат:
а) А(2; − |
2π |
) и В(6; π ); |
б) А(3; π ) и В(5; |
3π |
). |
|
4 |
||||
3 |
3 |
4 |
|
||
Найти полярные координаты середины отрезка АВ.
32

Задачи для самостоятельной работы
104. |
|
|
|
|
|
|
π |
|
4; − |
π |
|
|
5; − |
5π |
|
Даны точки в полярной системе координат: А 2; |
, B |
|
|
, C |
|
. |
|||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
2 |
|
|
|
7 |
|
Найти их прямоугольные координаты. |
|
|
|
|
|
|
|
|
|
|
|||||
105. |
Даны точки в прямоугольной системе координат: М1(0;5), |
М2(–3;0), |
|||||||||||||
М3( |
|
;-1). Найти их полярные координаты. |
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
||||||
106. |
Найти полярные координаты точек, |
симметричных |
|
точкам |
|
(2; − π ), |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
(1; − |
2π |
), (3;0) относительно: а) полюса; |
б) полярной оси. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
107. |
Построить линии, заданные уравнениями: |
|
|
|
|
|
|
|
|
|
|||||
а) ϕ = 5π ; б) ρ = cosϕ ; в) ρ = sin 3ϕ .
6
4.3.Прямая на плоскости
φ– угол наклона прямой (рисунок 9), φ [0;π) . k=tg φ – угловой коэффициент, k (– ∞;+∞).
Рисунок 9
Стандартные уравнения прямой
Уравнение прямой с угловым коэффициентом:
y = kx + b
k – угловой коэффициент прямой,
b – отрезок, отсекаемый прямой на оси Oy.
Уравнение прямой с известным угловым коэффициентом, проходящей через заданную точку:
y − y0 = k(x − x0 )
k – угловой коэффициент прямой, ( x0 ; y0 ) – координаты заданной точки.
33

Уравнение прямой, проходящей через две заданные точки:
y − y1 |
= |
x − x1 |
y2 − y1 |
|
x2 − x1 |
( x1; y1 ) , ( x2 ; y2 ) – координаты заданных точек.
Уравнение прямой «в отрезках»:
x + y = 1 a b
a и b – отрезки, отсекаемые прямой на координатных осях.
Уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору:
A(x − x0 ) + B( y − y0 ) = 0 ( x0 ; y0 ) – координаты заданной точки.
n = ( A; B) – нормальный (перпендикулярный) вектор.
Уравнение прямой, проходящей через заданную точку параллельно данному вектору (каноническое уравнение):
x − x0 = y − y0 l m
( x0 ; y0 ) – координаты заданной точки.
а = (l; m) – направляющий (параллельный) вектор.
Параметрические уравнения прямой:
x = x0 + l t,y = y0 + mt.
( x0 ; y0 ) – координаты точки на прямой.
а = (l; m) – направляющий (параллельный) вектор. t – параметр, t (– ∞;+∞).
Общее уравнение прямой:
Ax + By + С = 0
А, В, С – некоторые числа, причём А2+В2≠0.
n = ( A; B) – нормальный (перпендикулярный) вектор. 34
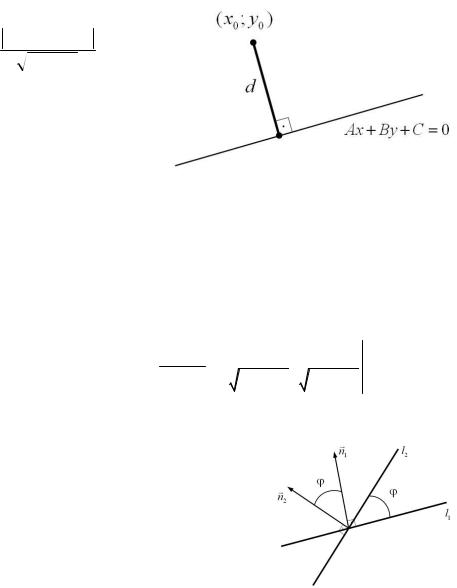
Частные случаи уравнения прямой:
y=b – уравнение прямой, параллельной оси Ox. y=0 – уравнение оси Ox.
x=a – уравнение прямой, параллельной оси Oy. x=0 – уравнение оси Oy.
y=kx – уравнение прямой, проходящей через начало координат.
Расстояние от точки до прямой
d = Ax0 + By0 + С

 A2 + B2
A2 + B2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 10 |
|||
|
|
|
|
|
|
|
|
Угол между прямыми |
|
|
|
||||||||||
|
|
k2 - k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
способ: tgϕ = |
|
|
, |
k , k |
2 |
- угловые коэффициенты прямых. |
||||||||||||||
|
|||||||||||||||||||||
|
|
1+ k2 k1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
A1 A2 + B1B2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
n1 n2 |
|
|
|
|
||||||||
2 |
способ (рисунок 11): |
cosϕ = cos n1 , n2 = |
|
|
|
|
|
= |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n1 |
× |
n2 |
|
|
|
A12 |
+ B12 × A22 + B22 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 : A1 x + B1 y + С1 = 0 n1 = ( A1; B1 ) - нормальные векторы прямых. l2 : A2 x + B2 y + С2 = 0 n2 = ( A2 ; B2 )
Условие параллельности прямых:
ℓ |
|
ℓ |
|
Û k |
= k |
|
|
|
|
|
|
|
|
1 |
|
2 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
B1 |
|
|
ℓ |
1 |
ℓ |
2 |
Û n n |
|
Û |
|
= |
|
|
|
|
|
|||||||||
|
|
1 |
2 |
|
A2 |
|
B2 |
||||
|
|
|
|
|
|
|
|
|
|
||
Условие перпендикулярности прямых:
|
^ ℓ2 |
Û k1 |
= - |
1 |
Рисунок 11 |
|
ℓ1 |
|
|||||
k2 |
||||||
|
|
|
|
|
||
|
|
|
|
|||
^ ℓ2 |
Û n1 |
^ n2 Û A1 A2 + B1 B2 = 0 |
||||
ℓ1 |
||||||
35
ЗАДАЧИ Для аудиторной работы
108.Дано уравнение прямой: 6х − 3y − 8 = 0 .
а) Найти угловой коэффициент прямой; б) привести данное уравнение к уравнению «в отрезках»; в) построить прямую.
109.Дано уравнение прямой с угловым коэффициентом:
y = − 53 x + 4 .
Привести данное уравнение к общему уравнению и к уравнению «в отрезках».
110.Составить уравнение прямой, проходящей через точку А(2;3): а) параллельно оси Ох;
б) параллельно оси Оy;
в) составляющей с осью Ох угол 45°.
111.Найти уравнение прямой, проходящей через точку А(6;-3) и середину отрезка CD, если С(2;-1), D(6;3).
112.Среди прямых
2x − 3y − 2 = 0, −3x − 2 y + 5 = 0, 4x − 6 y + 7 = 0,
2x + 3y − 8 = 0,
9x − 6 y + 5 = 0
указать параллельные и перпендикулярные.
113.Найти уравнение прямой, проходящей через точку М(-4;5) параллельно прямой 3x–5y+2=0.
114.Найти уравнение прямой, проходящей через точку N(6;–2) перпендикулярно прямой 4x+7y–1=0.
115.Найти угол между прямыми 2x–4y+5=0 и 3x–2y–3=0.
116.Дан треугольник АВС: А(–7;5), В(5;–4), С(3;10). Найти:
36

1)уравнение медианы АЕ;
2)уравнение высоты CD;
3)длину высоты CD.
117.Найти координаты точки А, симметричной точке В(5;7) относительно прямой x+2y–4=0.
118.Проверить, лежат ли точки А, В, С на одной прямой: А(–2;4), В(3;1),
С(5;0).
119.Найти уравнение прямой, проходящей через точку А(6;4) и отсекающей от координатного угла треугольник площадью 6 кв. ед.
120.Найти расстояние между двумя параллельными прямыми: 3x+4y–12=0 и
6x+8y+17=0.
121. Построить на плоскости область решений неравенств и их систем:
2x + y -1³ 0,
x
а) 4x–2y+5 ≤0; б) − y − 2 < 0,
2
y −1 > 0.
Задачи для самостоятельной работы
122.Найти уравнение прямой, имеющей угол наклона 60° и отсекающей на оси Ох отрезок, равный 3 ед.
123.Найти уравнение прямой, проходящей через точку пересечения прямых
3x–2y+4=0 и х+2=0 параллельно прямой 5x–6y+8=0.
124.Даны точки А(2;5), В(–3;1), С(0;8) и D(–2;4). Найти уравнение прямой, проходящей через середины отрезков АВ и CD.
125.Найти уравнение прямой, проходящей через точку А(5;–2):
а) перпендикулярно прямой 5x–y+1=0; б) под углом 45° к прямой 5x–y+1=0.
37
126.Дан треугольник АВС: А(0;4), В(–3;0), С(0;6). Найти проекцию вершины А на сторону ВС.
127.Найти площадь треугольника, ограниченного прямыми x–2y+6=0, 5x+y– 25=0 и осью Ох.
4.4.Кривые 2-го порядка
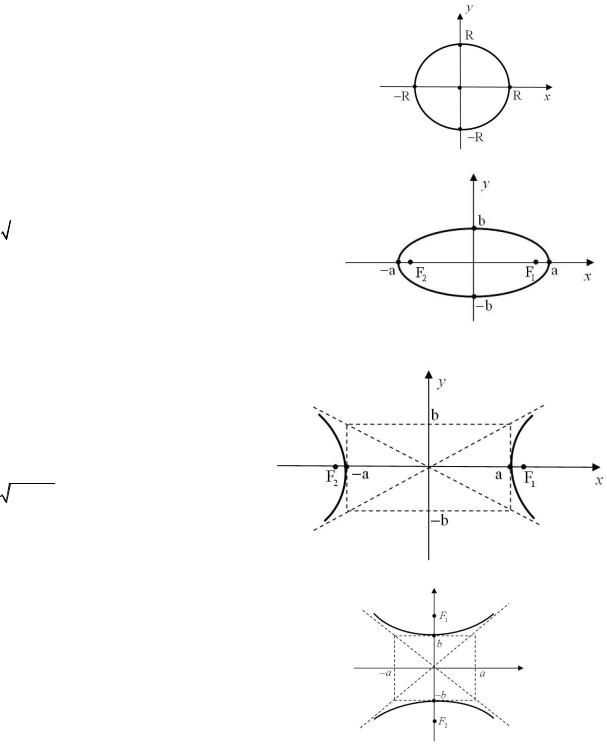
Окружность: х2 + y2 = R2
|
|
|
|
|
|
|
|
|
|
|
R – радиус окружности. |
|
|
|
|
|||||
Эллипс: |
x2 |
|
+ |
|
y2 |
= 1 |
|
|
|
|
|
Рисунок 12 |
||||||||
a2 |
b2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а – |
большая полуось, b – малая полуось (a>b). |
|
|
|||||||||||||||||
c = |
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
||||||
|
|
a2 − b2 |
половина межфокусного расстояния. |
|
||||||||||||||||
F1 (c;0), F2 (−c;0) – |
фокусы. |
|
|
|
|
|||||||||||||||
ε = |
с |
– эксцентриситет (0≤ε≤1). |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||
Еслиав уравнении эллипса a<b, то эллипс «вытянут» |
|
|||||||||||||||||||
по оси Oy, фокусы эллипса также находятся на этой оси. |
Рисунок 13 |
|||||||||||||||||||
Гипербола: |
|
|
x2 |
|
− |
y2 |
= 1 |
|
|
|
|
|
||||||||
|
a2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
|||||
а – |
действительная полуось, |
|
|
|
|
|||||||||||||||
b – |
мнимая полуось. |
|
|
|
|
|||||||||||||||
c = |
|
|
|
– |
половина межфокусного |
|
|
|
|
|||||||||||
|
|
a2 + b2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
расстояния. |
|
|
|
|
|||||||
F1 (c;0), F2 (−c;0) – |
фокусы. |
|
|
|
|
|||||||||||||||
ε = |
с |
– эксцентриситет (ε>1). |
|
|
|
Рисунок 14 |
||||||||||||||
|
|
|
|
|||||||||||||||||
Еслиауравнение гиперболы имеет вид |
y2 |
|
x2 |
, |
|
|||||||||||||||
b2 |
− a2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 |
|
|||
то гипербола называется сопряжённой (рисунок 15). |
|
|||||||||||||||||||
Рисунок 15
38

y2 |
= 2 px ( ) |
||
Парабола: |
x2 |
= 2 py (−↓) |
|
|
|||
|
|
|
|
|
|
|
р > 0 ветви →, − |
p − параметр |
|
|
|
|
р < 0 ветви ←, ↓ |
||
|
|
|
|
|
|
|
|
Для параболы с ветвями
Для параболы с ветвями −↓
|
p |
; 0 |
|
− фокус |
||||
F |
|
|
||||||
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
||
x = − |
|
|
|
|
− директриса |
|||
2 |
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
p |
− фокус |
||||
F 0; |
|
|
|
|
||||
|
|
|||||||
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
Рисунок 16 |
|
|
|
|
p |
|
|||
|
|
|
|
|
||||
y = − |
|
|
|
|
− директриса |
|||
2 |
|
|
||||||
|
|
|
|
|
|
|
||
Уравнения смещённых кривых:
( x − x |
)2 |
+ ( y − y )2 |
|
|
|
|
|
|
|
|||
= R2 − окружность |
|
|
|
|
||||||||
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
( x − x0 )2 |
|
( y − y0 )2 |
|
|
|
|
|
|
||||
+ |
|
= 1− эллипс |
|
( x ; y |
0 |
) − центр |
||||||
a |
2 |
|
|
b |
2 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
( x − x0 )2 |
− |
( y − y0 )2 |
|
= 1− гипербола |
|
|
|
|
|
|||
a2 |
|
b2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
( y − y |
)2 |
= 2 р( x − x |
) − парабола |
( x ; y |
) − вершина |
|||||||
|
0 |
|
|
|
|
0 |
|
|||||
( x − x0 )2 |
|
|
|
|
|
0 |
0 |
|
|
|
||
= 2 р( y − y0 ) − парабола −↓ |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Оптические свойства эллипса, гиперболы, параболы Если эллипс, гиперболу и параболу вращать вокруг фокальной оси (оси, на
которой находятся фокусы), то получим поверхности вращения, называемые соответственно эллипсоидом, гиперболоидом и параболоидом.
Эллипс: если источник света поместить в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе (рисунок 17).
Рисунок 17
39
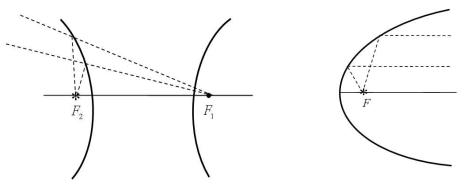
Гипербола: если источник света поместить в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, далее идут так, как если бы они шли из другого фокуса (рисунок 18).
Парабола: если источник света поместить в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно оси параболы (рису-
нок 19).
Рисунок 18 |
Рисунок 19 |
ЗАДАЧИ
Для аудиторной работы
128.Написать уравнение окружности, проходящей через точку А(4;–6), центр которой находится в точке С(–2;3).
129.Написать уравнение окружности, для которой отрезок АВ является диа-
метром: А(3;7), В(–1;9).
130.Построить эллипс: 9x2+25y2–225=0. Найти его полуоси, координаты фокусов, эксцентриситет.
131.Написать каноническое уравнение эллипса, если:
а) расстояние между фокусами равно 8, а малая полуось равна 3; б) большая полуось равна 6, а эксцентриситет равен 0,5.
132. Написать каноническое уравнение эллипса, проходящего через точки
М1(2;0) и М2(1;2).
133. Построить гиперболу: 16x2–9y 2–144=0. Найти его полуоси, координаты фокусов, эксцентриситет, уравнения асимптот.
40
