
математика
.pdf
Метод Гаусса решения систем линейных уравнений
(применим для систем с любым числом уравнений и неизвестных)
a х + a y + a z = b , |
a |
a |
|||
11 |
12 |
13 |
1 |
11 |
12 |
a21 х + a22 y + a23 z = b2 , A |
В = a21 |
a22 |
|||
|
х + a32 y + a33 z = b3. |
|
a32 |
||
a31 |
a31 |
||||
a13 |
|
b1 |
|
a23 |
|
b2 |
– расширенная матрица системы. |
a |
|
b |
|
33 |
|
3 |
|
|
1)Расширенную матрицу системы с помощью элементарных преобразований над строками приводят к ступенчатому виду:
* |
* |
* |
|
* |
|
|
|||||
|
|
* |
* |
|
|
|
0 |
|
* |
||
|
0 |
0 |
|
|
|
|
* |
|
* |
||
|
|
|
|||
2) Находят ранги основной и расширенной матриц и делают вывод о существовании и количестве решений (теорема Кронекера-Капелли):
r( A) = r( A B) = n единственное решение;
r( A) = r( A B) < n множество решений выражаем через (n - r) свободных переменных;
r( A) ¹ r( A B) решений нет.
3) По ступенчатой матрице записывают систему уравнений, и, начиная снизу, находят неизвестные x, y, z.
|
ЗАДАЧИ |
|
|
||||||
Для аудиторной работы |
|||||||||
11. Даны матрицы А и В. Найти 2А-В; А+ |
1 |
В: |
|
||||||
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
-2 |
1 |
|
|
4 |
-3 |
|
||
|
|
|
|
, В = |
|
|
|
|
|
А = |
1 3 |
|
|
0 1 |
. |
||||
|
0 |
5 |
|
|
|
6 |
-4 |
|
|
|
|
|
|
|
|||||
12. Найти АВ и ВА: |
|
|
|
|
|
|
|
|
|
|
5 |
3 |
, В = |
-6 |
3 |
4 |
|||
А = |
|
|
|
|
-1 2 |
. |
|||
|
-2 4 |
|
|
0 |
|||||
13. Найти матрицу D=АВ–( СТ)2:
11
3 |
|
2 |
2 |
0 |
1 |
3 |
||
4 |
|
1 |
3 |
|
||||
А = |
0 |
|
, В = |
|
, С = |
. |
||
1 |
5 |
|
0 |
5 |
|
0 |
4 |
|
|
|
|
|
|
|
|
||
14. Найти обратную матрицу к матрице А и сделать проверку: |
4 |
5 |
|
|
А = |
|
−3 |
. |
|
|
|
2 |
|
|
15. Решить систему линейных уравнений с помощью обратной матрицы:
а) 2x + 3y = |
|
|
x + 2 y + z = 8, |
|||
8, |
б) |
−2x + 3y − 3z = −5, |
||||
3x + 4 y = 11. |
|
3x − 4 y |
+ 5z |
= 10. |
||
|
|
|
||||
|
|
|
|
|
|
|
16. Найти ранг матриц: |
|
|
|
|
|
|
|
3 |
6 |
2 |
5 |
6 |
|
|
|
4 |
−1 |
|
||
|
А = |
, |
В = |
5 . |
||
|
2 |
4 |
|
2 |
−6 |
|
|
|
|
|
−1 |
||
17. Решить систему уравнений методом Гаусса: |
|
|||||
а) 2x + 3y = 8, |
x + 2 y + z = 8, |
|
|
|
2α − 3β − γ + 6 = 0, |
|
б) −2x + 3y − 3z = −5, |
|
|
в) 3α + 4β + 3γ + 5 = 0, |
|||
|
|
|
|
|
|
|
3x + 4 y = 11. |
3x − 4 y + 5z = 10. |
|
|
α + β + γ + 2 = 0. |
||
|
|
|
||||
2x + y − z = 1, |
x + y + z = 1, |
|
|
|
|
|
г) 3x + 2 y + 5z = 5, |
д) 2x + y + z = 2, |
|
|
|
|
|
−4x − 2 y + 2z = 6. |
3x + 2 y + 2z = 3. |
|
|
|
||
|
|
|
|
|
|
|
Дополнительные задачи
18. Даны матрицы А, В, С. Найти АВС–3 Е:
1 |
2 |
−3 |
|
1 |
|
|
||
|
|
|
|
|
|
|
|
, С = (2 0 5). |
А = |
1 |
0 |
2 |
|
, В = |
2 |
|
|
|
4 5 |
3 |
|
|
1 |
|
|
|
|
|
|
|
|
||||
19. При каких значениях λ матрица А не имеет обратной матрицы?
λ |
4 |
1 |
|
|
|
|
|
|
|
А = |
2 |
5 |
−1 . |
|
|
0 |
λ |
1 |
|
|
|
|||
20. При каких значениях λ ранг матрицы А равен трём?
2 |
3 |
−1 |
||
|
|
λ |
|
|
А = |
1 |
5 |
. |
|
|
3 |
4 |
1 |
|
|
|
|||
21. Решить систему уравнений методом Гаусса:
12
а) 3x1 + 4x3 − 3x4 = 0,2x1 − x2 − x3 = 0,
x + 2 y − z = 2,
б) 2x − 3y + 2z = 2,
3x + y + z = 8.
22. Найти матрицу А3 и её след:
23. Найти значение многочлена f(х) от матрицы А:
|
|
1 |
−2 |
|
f (x) = 3x |
2 |
|
2 |
−4 |
|
− 2x + 5, А = |
|||
|
|
|
3 |
−5 |
|
|
|
||
3 |
|
|
|
1 |
. |
2 |
|
|
24. Решить матричное уравнение:
−1 |
1 |
−2 |
−1 |
||
Х |
3 |
|
= |
3 |
. |
|
−4 |
|
4 |
||
25.Два вида продукта продаются в трёх магазинах. Матрица А – объёмы продаж в 1-м квартале, В – во 2-м. Найти объём продаж за 2 квартала и прирост продаж во 2-м квартале.
|
2 |
3 |
|
|
3 |
2 |
|
||
А = |
|
|
|
|
, В = |
|
|
|
|
|
5 |
1 |
|
|
4 |
2 |
. |
||
|
|
|
|
|
|
|
|
1 |
|
|
4 |
2 |
|
1 |
|
||||
26.Предприятие производит три типа продукции, используя два вида ресурсов. Норма затрат ресурсов i-го вида на производство единицы продукции j-го вида задана матрицей А, выпуск продукции за квартал – матрицей Х, стоимость единицы каждого вида ресурсов – матрицей Р. Найти:
а) матрицу S полных затрат ресурсов каждого вида; б) полную стоимость всех затраченных ресурсов.
2 |
1 |
1 |
10 |
|
|
||
|
|
|
, Р = (5 2). |
||||
А = |
1 |
2 |
|
, Х = |
20 |
|
|
|
3 |
|
10 |
|
|
||
|
|
|
|
|
|
|
|
27.Фирмой было выделено 236 тыс. руб. для покупки 29 предметов для офиса: компьютеров по цене 20 тыс. руб., столов (8,5 тыс. руб.), стульев (1,5 тыс. руб.). Позже выяснилось, что есть возможность приобрести компьютеры и столы немного дешевле: по 19,5 и 8 тыс. руб. соответственно, в результате чего можно будет купить ещё 1 стол. Сколько компьютеров, столов и стульев было приобретено?
13
Задачи для самостоятельной работы
28. Найти АВ и ВА:
а) |
3 |
−5 |
1 |
3 |
|
|
||
А = |
−7 |
|
, В = |
−1 |
1 |
|
; |
|
|
|
9 |
|
|
|
|||
1 б) А = −1 , В = (1 0 4).
2
29. Проверить, являются ли взаимно обратными матрицы:
|
2 |
3 |
4 |
−3 |
|
|
А = |
|
, В = |
−1 |
. |
|
2 |
7 |
|
2 |
|
30. Решить систему линейных уравнений |
с |
помощью обратной матрицы: |
|||
2x − 4 y + 3z = 1, |
|
|
|
|
|
|
= 3, |
|
|
|
|
x − 2 y + 4z |
|
|
|
|
|
3x − y + 5z = 2.
31. Решить систему уравнений методом Гаусса:
2x − 4 y + 3z = 1,
а) x − 2 y + 4z = 3,
3x − y + 5z = 2.
3x − 2 y + z = 1, б) x + y − 2z = 7,
5x − 3z = 2.
x − y + z = 2,
в) 2x − 2 y + 2z = 4,
x − 3y + z = 1.
32.Предприятие выпускает три вида продукции, используя два вида сырья. Нормы расходов сырья на единицу продукции заданы матрицей А. Определить денежные расходы предприятия на выпуск товаров, заданный матрицей С, если стоимость единицы каждого вида сырья выражена матрицей Р.
2 |
|
1 |
|
1 |
|
|
|
3 |
|
|
|
, Р = (2 3). |
|||
А = |
1 |
4 |
|
, С = |
1 |
|
|
|
2 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
14
|
|
|
|
|
1.3. Модель Леонтьева многоотраслевой экономики |
|||
X = AX + Y или (E − A) X = Y – соотношения стоимостного межотраслевого ба- |
||||||||
ланса. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
– |
вектор валового выпуска, x – объём валового продукта i-й отрас- |
|||||
x2 |
|
|||||||
X = ... |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||
|
|
ли. |
|
|
|
|||
xn |
|
|
|
|
|
|
|
|
a11 |
|
a12 |
... |
|
a1n |
|
||
|
|
a22 |
|
|
|
|
– матрица прямых затрат, аij – затраты продукции i-й |
|
А = a 21 |
|
... |
|
a2 n |
||||
... |
|
... |
... |
|
... |
отрасли на производство единицы продукции j-й отрас- |
||
|
|
a n 2 |
... |
|
|
|||
an1 |
|
|
ann |
|
||||
ли, a |
= |
xij |
, х |
ij |
– объём продукции i-й отрасли, потребляемый j-й отраслью в |
|||
|
||||||||
|
ij |
|
x j |
|
|
|||
|
|
|
|
|
|
|||
процессе производства. |
||||||||
y |
|
|
|
|
|
|
|
|
1 |
|
– |
вектор конечного продукта, yi – объём продукта i-й отрасли для |
|||||
y2 |
|
|||||||
Y = y |
|
непроизводственного потребления. |
||||||
3 |
|
|||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|
|
Из соотношений межотраслевого баланса X = (E − A)−1Y = SY. |
||||||||
S = (E − A)−1 – |
матрица полных затрат, sij – величина валового выпуска про- |
|||||||
дукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли.
Матрица прямых затрат А (аij≥0) называется продуктивной, если для любого вектора конечного продукта Y (yi≥0) существует вектор валового выпуска X (xi ≥0).
n
Критерий продуктивности: 1) max ∑ aij ≤ 1 (максимум сумм элементов
i=1
столбцов матрицы А не превосходит 1);
n
2) j : ∑ aij < 1 (хотя бы для одного столбца сумма элементов строго меньше
i=1
1).
15
ЗАДАЧИ Для аудиторной работы
33. Какие из данных матриц являются продуктивными?
0, 3 |
|
0, 6 |
0,8 |
0,1 |
0,1 |
0, 2 |
0, 4 |
||
|
|
|
|
|
|
||||
A = |
|
, |
B = |
, |
C = |
0, 5 0, 3 |
0, 2 |
. |
|
0, 4 |
|
0, 4 |
0, 2 |
0, 9 |
|
0, 2 |
0, 5 |
0, 6 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0,3 |
0,8 |
Найти: |
|
34. Дана матрица прямых затрат А = |
|
. |
|||||||
|
|
|
|
|
|
0,5 |
0, 2 |
|
|
а) вектор валового выпуска Х для обеспечения конечной продукции |
|||||||||
350 |
|
|
|
|
|
|
|
|
|
Y = |
|
; |
|
|
|
|
|
|
|
180 |
|
|
|
|
|
|
|
|
|
б) приращение вектора ∆Х для увеличения выпуска конечной продук- |
|||||||||
ции на |
|
100 |
|
|
|
|
|
|
|
|
Y = |
. |
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
35. Имеются данные о работе системы двух отраслей в течение некоторого периода:
|
Потребление |
Конечный продукт |
|
|
|
|
|
|
1 отрасль |
2 отрасль |
|
|
|
||
|
|
|
|
Производство, 1 отрасль |
75 |
210 |
90 |
|
|
|
|
Производство, 2 отрасль |
120 |
105 |
195 |
|
|
|
|
Найти матрицы прямых и полных затрат.
36. В таблице приведены данные об исполнении баланса за отчётный период.
|
Потребление |
Конечный продукт |
|
|
|
|
|
|
1 отрасль |
2 отрасль |
|
|
|
||
|
|
|
|
Производство, 1 отрасль |
45 |
140 |
175 |
|
|
|
|
Производство, 2 отрасль |
180 |
210 |
170 |
|
|
|
|
Вычислить необходимый объём валового выпуска каждой отрасли, если конечный продукт 1-й отрасли должен увеличиться на 30%, а 2-й отрасли – в 2,5 раза.
16
Задачи для самостоятельной работы
37. Какие из данных матриц являются продуктивными? |
||||||||
0, 7 |
0, 5 |
|
|
0, 3 |
0,1 |
0, 2 |
|
|
, |
|
0, 2 |
0, 7 |
0, 3 |
|
|||
A = |
0, 5 |
|
B = |
. |
||||
0, 2 |
|
|
|
0,1 |
0,1 |
0, 4 |
|
|
|
|
|
|
|
|
|||
38. Дана матрица прямых затрат |
0, 5 |
0,1 |
|
. Найти вектор валового выпус- |
А = |
|
|
||
|
0, 2 |
0, 4 |
|
|
ка Х для обеспечения конечной продукции Y = 115 .
325
39.Имеются данные о работе системы двух отраслей в течение некоторого периода:
|
Потребление |
Конечный продукт |
|
|
|
|
|
|
1 отрасль |
2 отрасль |
|
|
|
||
|
|
|
|
Производство, 1 отрасль |
120 |
40 |
40 |
|
|
|
|
Производство, 2 отрасль |
80 |
200 |
120 |
|
|
|
|
Найти матрицы прямых и полных затрат.
40. В таблице приведены данные об исполнении баланса за отчётный период.
|
|
Потребление |
|
Конечный |
|
|
|
|
|
|
1 отрасль |
2 отрасль |
3 отрасль |
продукт |
|
|
|||
|
|
|
|
|
Производство, 1 отрасль |
5 |
3 |
1 |
1 |
|
|
|
|
|
Производство, 2 отрасль |
7 |
4 |
5 |
4 |
|
|
|
|
|
Производство, 3 отрасль |
6 |
2 |
4 |
8 |
|
|
|
|
|
Вычислить необходимый объём валового выпуска каждой отрасли, если конечный продукт 1-й отрасли должен увеличиться в 2 раза, 2-й отрасли – на
30%, а 3-й – на 50%.
17
Вопросы для самоконтроля по главе 1 «Определители. Матрицы. Системы линейных уравнений»
1.Как вычисляются определители 2-го, 3-го, 4-го порядков?
2.Какие свойства определителей существуют?
3.Что такое минор и алгебраическое дополнение элемента определителя?
4.Что называется решением системы уравнений?
5.Какая система называется совместной, несовместной, однородной, неоднородной?
6.Как решить систему линейных уравнений с помощью определителей? Как называется этот метод решения? Любую ли систему можно решить этим методом?
7.Какие виды матриц существуют?
8.Любые ли матрицы можно сложить, вычесть, перемножить? Как выполняются эти действия?
9.Как найти обратную матрицу? Для любой ли матрицы существует обратная? Как проверить, верно ли найдена обратная матрица?
10.Как применить обратную матрицу для решения системы линейных уравнений? Любые ли системы линейных уравнений можно решить с помощью обратной матрицы?
11.Что называется рангом матрицы? Как его найти?
12.В чём состоит метод Гаусса решения систем линейных уравнений?
13.Какие уравнения называют соотношениями баланса? Как их записать в матричном виде?
14.Какова основная задача межотраслевого баланса? Как её решить?
15.Какая матрица называется матрицей прямых затрат, полных затрат?
16.Как проверить продуктивность матрицы прямых затрат?
18
ГЛАВА 2. ВЕКТОРЫ
2.1. Основные действия над векторами
Вектор – это направленный отрезок.
Если А(х1;y1;z1), В(х2;y2;z2), то AB = ( x2 − x1; y2 − y1; z2 − z1 ) – координаты вектора.
a =
a =
(x; y; z) a =
cos
(x; y; z) cos
cos

 x2 + y2 + z2 – модуль (длина) вектора.
x2 + y2 + z2 – модуль (длина) вектора.
α= x a
β = y – направляющие косинусы вектора.
a
γ= z a
Действия над векторами
1) Сложение (вычитание):
a = ( x1; y1; z1 ), b = ( x2 ; y2 ; z2 ) a ± b = ( x1 ± x2 ; y1 ± y2 ; z1 ± z2 ).
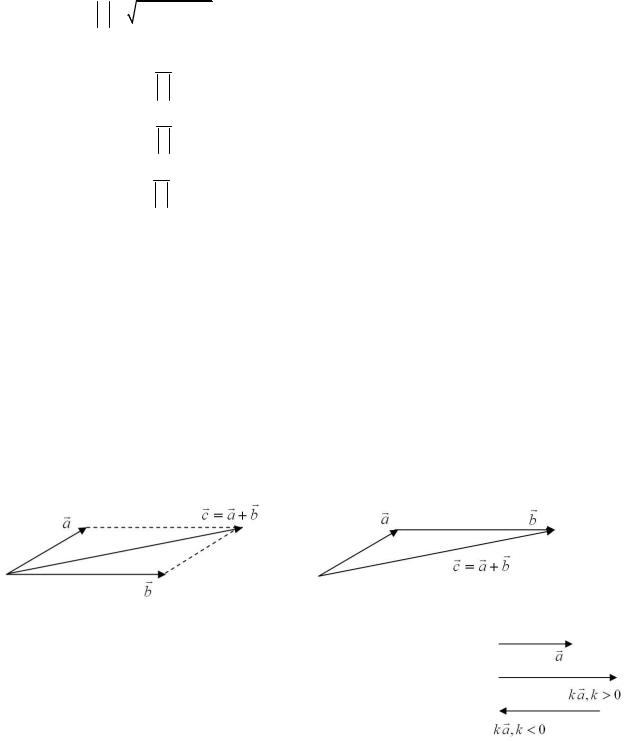
Геометрически: применяются правила «параллелограмма» (рисунок 1): сумма двух векторов есть вектор, идущий из общего начала векторов по диагонали параллелограмма, построенного на этих векторах; или «треугольника» (рисунок 2): сумма двух векторов есть вектор, идущий из начала первого вектора в конец второго при условии, что складываемые векторы приложены друг к другу (второй вектор выходит из конца первого). В случае суммы нескольких векторов применяется правило «многоугольника»: сумма n векторов есть вектор, идущий из начала первого вектора в конец последнего при условии, что складываемые векторы приложены друг к другу.
Рисунок 1 |
Рисунок 2 |
2) Умножение на число: |
|
a = ( x; y; z ) k a = (kx; ky; kz ), где k − число. |
|
Геометрически: длина вектора изменяется в |k| раз, направление |
|
меняется в зависимости от знака k. Т.е. в результате получаем |
|
вектор, коллинеарный данному (рисунок 3). |
Рисунок 3 |
19 |
|
3) Скалярное произведение:
a = ( x1; y1; z1 ) , b = ( x2 ; y2 ; z2 ) a ×b = x1 x2 + y1 y2 + z1 z2 .
|
|
× |
|
cosϕ , |
Геометрически (рисунок 4): ab = |
a |
b |
||
|
|
|
|
|
где φ – угол между векторами.
|
|
|
|
|
|
|
|
|
Рисунок 4 |
|
|
|
|||
4) |
Угол между векторами: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
cosϕ = |
a b |
ϕ = arccos |
a b |
|
|
|
|
|
|
|
||||
|
|
a × b |
|
|
|
|
a × b |
|
|
|
|
|
|
|
|
5) |
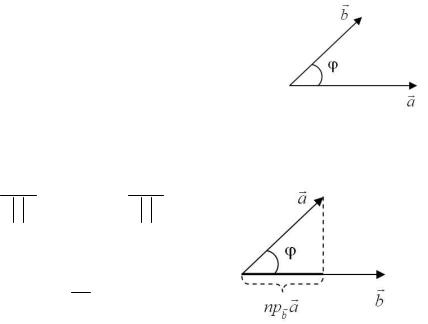
Проекция вектора на вектор (рисунок 5): |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a b |
|
|
|
|
|
|
||||||||
|
|
|
пр a = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Рисунок 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
y |
|
z |
|||||
Условие коллинеарности (параллельности) векторов: a b Û |
1 |
= |
1 |
= |
1 |
. |
|||||||||
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
y2 |
|
z2 |
|
Условие ортогональности (перпендикулярности): a ^ b Û a ×b = 0 Û x1 x2 + y1 y2 = 0.
Векторное пространство. Разложение вектора по базису
1) Запись вектора в системе орт: a = (x; y; z) a = xi + y j + zk , где i, j, k – орты
(единичные векторы) координатных осей. 2) Разложение вектора по базису:
a = α1a1 +α2a2 +α3a3 .
a1 , a2 , a3 – базисные векторы, α1 ,α2 ,α3 – коэффициенты разложения (координа-
ты вектора a в базисе a1 , a2 , a3 ).
Примечание:
а) векторы a1 , a2 ,..., an образуют базис n-мерного линейного пространства, если определитель, составленный из их координат, не равен нулю; б) векторным (линейным) пространством называется множество векторов с
действительными координатами, в котором определены линейные операции
20
