математика
.pdf(сложение, вычитание, умножение на число), удовлетворяющие следующим условиям:
° |
x + y = y + x – коммутативность суммы (переместительный закон); |
|
° |
( x + y ) + z = x + ( y + z ) – |
ассоциативность суммы (сочетательный закон); |
° |
α (β x ) = (αβ ) x – ассоциативность (сочетательный закон) относительно |
|
|
числового множителя; |
|
° |
(α + β ) x = α x + β x – |
дистрибутивность относительно суммы числовых |
множителей;
°x + 0 = x ;
°x + (−x) = 0 ;
°1× x = x.
ЗАДАЧИ
Для аудиторной работы
41.Даны точки А(1;3;2) и В(5;8;1). Найти координаты векторов АВ и ВА, на-
правляющие косинусы вектора АВ.
42.Определить координаты начала вектора a = (2; −3; −1), если его конец нахо-
дится в точке В(1;-1;2).
43.Может ли вектор образовывать с осями координат углы:
а) 90°, 150° и 60°; б) 45°, 135° и 60°?
44.Вектор, модуль которого равен 2, образует с осями координат углы 45°, 60° и 120° соответственно. Найти координаты вектора.
45.Даны векторы a и b. Изобразить векторы c = a + 2b и d = 3a − b.
Пусть a = (−1; 2), b = (3;5). Найти координаты и модули векторов c и d.
46. На векторах ОА = (1;1;0) и ОВ = (0; −3;1) построен параллелограмм. Найти
длины его диагоналей.
47.Коллинеарны ли векторы a = (6;3; −2) и b = (−12; −6; 4) ?
48.При каких α и β векторы a = (4;3;α ) и b = (2; β ; −1) коллинеарны?
21
49. Найти скалярное произведение векторов a и b, если a = 4i − 2 j − 4k,
b = 6i − 3 j + 2k.
50.Известны модули векторов: a = 3, b = 4. Угол между векторами равен 60°.
Вычислить:
а) a b;
б) (2a − b)(a + 3b); в) (a + 2b)2 .
51. Найти угол между векторами:
|
|
|
|
|
|
|
|
а) a = 3i |
+ 5 j и b = 2i |
− 4 j + k; |
|||||
|
|
|
|
|
|
|
|
б) a = i |
+ 2 j + 3k и b = 6i + 4 j − 2k. |
||||||
52.Найти проекцию вектора a = (5; 2;5) на вектор b = (2; −1; 2).
53.При каком α векторы a = (α ; −3; 2) и b = (1; 2; −α ) перпендикулярны?
54.Образуют ли векторы базис двумерного пространства:
|
−5) |
|
а) a = (1; |
и b = (4;3); |
б) a = 3i + 6 j и b = 4i + 8 j ?
55.Образуют ли векторы базис трёхмерного пространства:
a= (−5;3;1), b = (2; 0; −3), c = (3;1; 2) ?
56.Образуют ли векторы a = (−3; 4) и b = (2;5) базис двумерного пространства?
Если образуют, то выразить вектор с = (12;7) через векторы a и b .
57.Образуют ли векторы a, b, c базис трёхмерного пространства? Если обра-
зуют, то найти координаты вектора х в этом базисе:
|
|
|
|
|
a = 2 j + k , |
|
|
||
|
|
|
|
|
b = |
j − k |
|
|
|
|
|
|
|
|
c = |
5i − 3 j |
+ 2k , |
||
|
|
|
|
|
x = 15i |
− 20 j |
− k . |
||
22
Задачи для самостоятельной работы
58.Даны точки А(-1;3;5) и В(-2;0;6). Найти координаты и модули векторов
АВ и ВА, направляющие косинусы вектора АВ.
59. Даны две координаты вектора a : x = 4, y = −12. Найти его третью координа-
ту z, если a = 13.
60.Вектор составляет с осями Ox и Oz углы 120° и 45° соответственно. Какой угол образует вектор с осью Оy?
61.В треугольнике АВС сторона АВ поделена на три равные части точками M
и N. Пусть СА = a и СВ = b. Выразить вектор СM через векторы a и b.
|
2 |
если m и n – |
единичные векторы, угол между которы- |
62. Вычислить (m + n) |
, |
ми равен 30°.
63.Найти угол между диагоналями параллелограмма, построенного на векто-
рах a = (2;1;0) и b = (0; −2;1).
64. Найти проекцию вектора a на вектор b + c, если a = (1; −3; 4), b = (3; −4; 2),
c= (−1;1; 4).
65.Даны векторы a = (3; −5) и b = (2;1) . Проверить, образуют ли векторы базис двумерного пространства. Если образуют, то выразить вектор с = (5; −17)
через векторы a и b .
66.Даны векторы a, b, c . Проверить, образуют ли векторы базис трёхмерного пространства. Если образуют, то найти координаты вектора х в этом базисе.
a = (1; 2; −3); b = (4;1;5); c = (2; 0;1); x = (4; −3;12).
23
|
|
|
|
|
|
|
|
|
|
|
2.2. Линейные операторы |
|
|||||
y = Аɶ(х) |
– линейный оператор, переводящий вектор х = (x , x ,..., x ) (прообраз) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
n |
в вектор y = ( y1 , y2 ,..., yn ) (образ). |
|
|
|
|
|
||||||||||||
a |
|
a |
... |
a |
|
|
y = a |
х + a |
x |
+ ... + a |
x , |
|
|||||
|
11 |
12 |
|
1n |
|
1 |
11 1 12 2 |
|
1n n |
|
|||||||
A = a21 |
a22 |
... |
a2n |
y2 |
= a21 х1 + a22 x2 + ... + a2n xn , Y = AX . |
|
|||||||||||
... |
... |
... |
... |
|
............................................ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
... |
a |
|
y |
|
= a |
х + a |
x |
|
+ ... + a x , |
|
|||
|
n1 |
n 2 |
nn |
n |
|
|
|||||||||||
|
|
|
|
|
|
n1 1 |
n 2 2 |
|
nn n |
|
|||||||
↑
матрица линейного оператора Вектор х ¹ 0 – собственный вектор оператора Аɶ , если существует число λ
(собственное значение оператора), такое, что Аɶ(х) = λ х .
Собственные значения находят из уравнения:
|
|
|
a11 − λ |
a12 |
... |
a1n |
|
|
|
|
|
||||
A − λ E |
|
= 0 |
a21 |
a22 − λ |
... |
a2n |
= 0. |
|
|||||||
|
|
|
......................................... |
|
|||
|
|
||||||
|
|
|
an1 |
an 2 |
... |
ann − λ |
|
Затем находят собственные векторы как решение системы уравнений (эта система всегда имеет множество решений):
(a11 − λ)х1 + a12 x2 + ... + a1n xn = 0, |
|||||
|
|
|
|
|
|
( A − λ E ) Х = 0 a21 х1 + (a22 − λ)x2 |
+ ... + a2n xn = 0, |
||||
..................................................... |
|||||
|
|
|
|
|
|
a |
х + a |
x + ... + (a |
nn |
− λ)x = 0. |
|
|
n1 1 |
n 2 2 |
|
n |
|
Если матрица оператора является диагональной, то все её диагональные элементы являются собственными значениями, и все векторы базиса являются собственными.
24
ЗАДАЧИ Для аудиторной работы
67. Проверить, является ли оператор Аɶ(х) линейным. Если является, записать
матрицу оператора:
а) Аɶ(х) = −3х;
б) Аɶ(х) = ( х1; х2 + 2х3 ; х3 ); в) Аɶ(х) = ( х1 х2 ; 0; −х3 ).
68. |
Найти координаты вектора y = Аɶ(х) , если оператор Аɶ(х) задан матрицей: |
||||||||
|
2 |
−1 |
|
0 |
0 |
1 |
|
|
|
|
|
|
1 |
1 |
2 |
|
|
||
|
а) А = |
|
, х = (1; 0); |
б) А = |
|
, х = (−1; 2;1). |
|||
|
3 |
4 |
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|||
69. |
Записать матрицу линейного оператора и найти образ вектора х = (2; −1;5) : |
||||||||
Аɶ(х) = ( х1 − 3х2 + х3 ; х2 + х3 ; 4х1 + х2 + х3 ) .
70.Найти собственные значения и собственные векторы линейного оператора
Аɶ(х) , заданного матрицей А:
2 |
4 |
|
|
1 |
2 |
−2 |
|
1 |
0 |
2 |
|
|
|
б) А = 1 |
|
3 |
|
в) А = 0 |
|
|
. |
||||
а) А = |
−1 |
−3 |
|
; |
0 |
; |
3 |
0 |
||||
|
|
|
|
3 |
|
|
|
0 |
|
|
||
|
|
|
|
|
1 |
0 |
|
0 |
0 |
|||
71.Вектор х является собственным вектором оператора А. Найти соответствующее собственное значение:
4 |
2 |
|
−5 |
|
|
A = |
−3 |
|
, Х = |
5 |
. |
|
−1 |
|
|
||
Задачи для самостоятельной работы
72. Выяснить, является ли оператор линейным:
а) Аɶ(х) = ( х1 − х2 ; х2 ; х3 ) ; б) Аɶ(х) = (х12 ; х2 ; х32 ).
25
73.Найти координаты вектора y = Аɶ(х) , если оператор Аɶ(х) задан матрицей:
А= −1 1 , х = (2; −1).
2 1
74.Найти собственные значения и собственные векторы линейного оператора
Аɶ(х) , заданного матрицей А:
3 |
−4 |
|
1 |
1 |
8 |
|
||
|
|
|
|
|
|
|||
а) А = |
−2 |
|
; |
б) А = |
0 2 |
0 |
. |
|
|
1 |
|
|
1 |
0 |
|
|
|
|
|
|
|
|
−1 |
|||
75.Вектор х является собственным вектором оператора А. Найти соответствующее собственное значение:
3 |
−2 |
|
1 |
|
|
A = |
2 |
|
, Х = |
2 |
. |
|
−2 |
|
|
||
Вопросы для самоконтроля по главе 2 «Векторы»
1.Что такое вектор? Как найти координаты вектора, зная координаты его начала и конца?
2.Как вычислить модуль вектора?
3.Что такое орт вектора? Как найти его координаты?
4.Что такое направляющие косинусы вектора? Как их найти?
5.Какие векторы называются равными, коллинеарными, сонаправленными, противоположно направленными, компланарными?
6.Как сложить/вычесть векторы, умножить вектор на число, если известны координаты векторов?
7.Что называется скалярным произведением векторов? Как его найти, если известны координаты векторов? Как скалярное произведение зависит от угла между векторами?
8.Как найти проекцию вектора на ось, на вектор?
9.Что является условием коллинеарности и перпендикулярности векторов?
26
10.Что такое векторное (линейное) пространство?
11.Что такое размерность пространства, базис?
12.Что такое линейная комбинация векторов? В каком случае векторы называются линейно независимыми? Линейно зависимыми?
13.Как проверить, образуют ли данные векторы базис пространства? Как разложить данный вектор по этому базису?
14.Что такое линейный оператор, образ, прообраз, матрица оператора?
15.Как найти образ заданного вектора, зная матрицу оператора?
16.Какой вектор называется собственным вектором линейного оператора?
17.Что такое собственное значение линейного оператора?
18.Как найти собственное значение и собственный вектор линейного оператора?
ГЛАВА 3. КВАДРАТИЧНЫЕ ФОРМЫ
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
L(x1 , x2 ,..., xn ) = ∑∑ aij xi x j |
= a11 x12 + a22 x22 + ... + ann xn2 + 2a12 x1 x2 + 2a13 x1 x3 + ... |
|||||||||||||
|
|
|
|
|
i=1 j =1 |
|
|
|
|
|
|
|
||
a |
11 |
a |
12 |
... |
a |
1n |
|
– |
|
матрица квадратичной формы. Элементы матрицы, |
||||
|
|
|
|
|
|
|||||||||
A = a21 |
a22 ... |
a2n |
симметричные относительно главной диагонали, сов- |
|||||||||||
... |
... ... |
... |
|
|||||||||||
|
|
an 2 ... |
ann |
|
падают: aij |
= a ji . |
||||||||
an1 |
|
|||||||||||||
L(x , x ,..., x ) = a |
x2 + a |
x |
2 |
+ ... + a |
nn |
x2 |
– каноническая квадратичная форма. |
|||||||
1 |
2 |
|
|
n |
11 1 |
|
22 |
2 |
|
n |
|
|||
L > 0 |
|
xi |
положительно определённая квадратичная форма. |
|||||||||||
L < 0 |
|
xi |
отрицательно определённая квадратичная форма. |
|||||||||||
Критерии знакоопределённости квадратичной формы:
1.L > 0 все собственные значения матрицы А положительны. L < 0 все собственные значения матрицы А отрицательны.
2.Критерий Сильвестра:
L > 0 все главные миноры ∆i матрицы А положительны.
L < 0 главные миноры ∆i матрицы А меняют знаки, начиная с «–».
27
1 = a11
|
|
|
|
a11 |
a12 |
|
|
|
|
|
= |
|
|
||
|
|
2 |
a21 |
a22 |
|
|
|
|
|
|
|
|
|
||
|
|
a |
a |
a |
– главные миноры матрицы А. |
||
|
|
|
|||||
|
|
|
|
11 |
12 |
13 |
|
|
|
= a21 |
a22 |
a23 |
|||
|
|
3 |
|||||
a a a
31 32 33
.........
ЗАДАЧИ
Для аудиторной работы
76. Написать матрицу квадратичной формы:
а) L = 3x2 |
− x2 |
+ 8x x − 6x x + 2x2 |
; |
|
||||||
|
1 |
2 |
1 |
2 |
|
2 |
3 |
3 |
|
|
б) L = 2x2 |
+ x2 |
− x2 |
+ x x − 3x x + 5x x ; |
|||||||
|
1 |
2 |
3 |
1 |
2 |
|
1 |
3 |
2 |
3 |
в)L = x2 |
−10x x . |
|
|
|
|
|
|
|
||
1 |
|
2 |
3 |
|
|
|
|
|
|
|
77. Написать квадратичную форму по заданной матрице:
7 |
|
|
|
2 1 |
6 |
|
|||
4 |
|
|
|
|
|
|
|||
а) А = |
4 |
1 |
|
; |
б) А = |
1 |
0 |
0 |
. |
|
|
|
|
6 |
0 |
|
|
||
|
|
|
|
|
|
−1 |
|||
78. Исследовать квадратичную форму на знакоопределённость:
а) L = x12 +10x22 − 4x1 x2 − 2x2 x3 + x32 ;
б) L = x12 + x22 + x32 + 4x1 x2 + 6x1 x3 + 4x2 x3 ;
в) L = −7x12 − x22 + 2x1 x3 + x2 x3 − x32 .
79.Найти значение m, при котором квадратичная форма является положительно определённой:
L= mx12 + x22 + 4x1 x2 − 2x2 x3 + mx32
80.Найти значение m, при котором квадратичная форма не является знакоопределённой:
L = 3m x12 − x22 +12x1 x2
28
Задачи для самостоятельной работы
81. Написать матрицу квадратичной формы:
а) L = 3x12 − 5x22 + 7x1 x2 +10x32 ;
б) L = x12 +18x1 x2 −11x1 x3 .
82.Написать квадратичную форму по заданной матрице:
|
0 |
−3, 5 |
|
5 |
1, 5 |
1 |
|
|
; |
|
|
2 |
0 |
|
|||
а) А = |
−3, 5 |
|
б) А = 1, 5 |
. |
||||
|
8 |
|
|
1 |
0 |
−9 |
|
|
|
|
|
|
|
|
|||
83. Исследовать квадратичную форму на знакоопределённость:
а) L = x12 + 4x1 x2 + 4x1 x3 + 5x22 + 4x2 x3 + 9x32 ; б) L = 10x12 + 3x22 − x32 + 2x1 x2 + 6x1 x3 + x2 x3 ; в) L = −5x12 − 3x22 − 2x2 x3 − x32 .
84.Найти значение m, при котором квадратичная форма является отрицательно определённой:
L =− x12 + 2mx22 + 4x1 x2 +10x2 x3 −x32
Вопросы для самоконтроля по главе 3 «Квадратичные формы»
1.Что такое квадратичная форма?
2.Как записать матрицу квадратичной формы?
3.Какая квадратичная форма называется канонической?
4.В каком случае квадратичная форма называется положительно определённой, отрицательно определённой?
5.Каковы критерии проверки знакоопределённости квадратичной формы?
29
Глава 4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
4.1. Прямоугольные координаты
Если А(х1; y1), В(х2; y2), то АВ = 
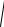( х2 − х1 )2 + ( y2 − y1 )2 – длина отрезка АВ,
|
|
x1 + λ x2 |
|||
x = |
|
|
|
|
|
|
1+ λ |
||||
|
|
y1 + λ y2 |
|||
|
|
||||
y = |
|
1+ λ |
|||
|
|
||||
|
|
x + x |
|||
x = |
|
1 2 |
|
|
|
2 |
|
|
|
||
|
|
y1 + y2 |
|
|
|
|
|
|
|||
y = |
2 |
|
|
|
|
|
|
|
|
||
– деление отрезка в соотношении λ (рисунок 6).
Рисунок 6
– координаты середины отрезка АВ.
A(x1 , y1 ) |
|
|
|
|
|
|
x2 − x1 |
|
− x1 |
|
||
|
|
|
|
|
|
|
|
|||||
|
, y2 ) SABC = |
1 |
|
|
|
|
= |
x3 |
|
|||
|
|
|
|
|
||||||||
Площадь треугольника: B(x2 |
|
|
|
, |
где |
y2 − y 1 |
y3 − y 1 |
. |
||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|||||
C(x3 |
, y3 ) |
|
|
|
|
|
|
|
|
|
|
|
ЗАДАЧИ
Для аудиторной работы
85.В треугольнике АВС вычислить длины сторон АВ и АС, если А(4;-5),
В(0;6), С(7;2).
86.Найти длину медианы АМ треугольника АВС, если А(5;-6), В(8;1), С(-2;9).
87.На оси ординат найти точку, отстоящую от точки А(4;-3) на расстоянии 5 ед.
88.Найти координаты точки, делящей отрезок CD в отношении 2:3, если С(-2;5), D(6;-3).
89.Найти координаты точек, делящих отрезок АВ на три равные части, если А(4;0), В(10;6).
90.Даны две вершины треугольника А(-5;1), В(1;9) и точка пересечения медиан К(1;5). Найти координаты третьей вершины.
30