математика

сти 2x+y+3z+5=0.

160.Найти проекцию точки К(2;0;1) на плоскость 3x+2y–z+23=0.

161.Найти координаты точки, симметричной точке А(3;4;–1) относительно плоскости 2x+3y–z–5=0.

162.Найти координаты точки, симметричной точке А(–1;4;7) относительно

Задачи для самостоятельной работы

163.Написать уравнение плоскости, проходящей через точку B(5;6;–1) параллельно плоскости 4x+2y–6z+3=0.

164.Найти площадь треугольника, образованного пересечением плоскости 2x+2y+3z–6=0 с координатными плоскостями.

165.Написать уравнение прямой, проходящей через точку А(3;5;–3) парал-

лельно вектору АВ , если В(2;1;7).

166.Написать уравнение прямой, проходящей через точку C(2;–6;3) перпендикулярно плоскости 5x+2y–z+5=0.

167.Написать уравнение плоскости, проходящей через точку A(6;–8;1) пер-

z = 2t + 2.

51

Вопросы для самоконтроля по главе 5 «Аналитическая геометрия в пространстве»

1.Что называется поверхностью в пространстве?

2.Что называется уравнением поверхности в пространстве?

3.Как называется вектор, перпендикулярный плоскости?

4.Напишите уравнение плоскости, проходящей через заданную точку перпендикулярно данному вектору.

5.Напишите уравнение плоскости «в отрезках». Как, пользуясь этим уравнением, построить плоскость?

6.Как, зная координаты трёх точек, лежащих на плоскости, составить её уравнение?

7.Напишите общее уравнение плоскости. Каков смысл числовых коэффициентов перед переменными в этом уравнении?

8.Напишите уравнения координатных плоскостей, уравнения плоскостей, параллельных координатным плоскостям.

9.Напишите уравнения плоскостей, проходящих через координатные оси, уравнения плоскостей, параллельных координатным осям.

10.Напишите уравнение плоскости, проходящей через начало координат.

11.Напишите формулу для вычисления расстояния от заданной точки до плоскости.

12.Как найти угол между двумя плоскостями?

13.Каким образом можно узнать, параллельны ли плоскости? перпендикулярны ли?

14.Напишите уравнение прямой в пространстве, проходящей через две заданные точки.

15.Как называется вектор, параллельный прямой?

16.Напишите канонические уравнения прямой в пространстве.

17.Напишите параметрические уравнения прямой в пространстве.

52

18.Как найти угол между двумя прямыми в пространстве?

19.Как составить уравнение прямой, проходящей через заданную точку перпендикулярно данной плоскости?

20.Как составить уравнение плоскости, проходящей через заданную точку перпендикулярно данной прямой?

21.Как найти координаты точки пересечения прямой и плоскости?

22.Как найти угол между прямой и плоскостью?

23.В каком случае прямая и плоскость параллельны? перпендикулярны?

ГЛАВА 6. КОМПЛЕКСНЫЕ ЧИСЛА

z = x + yi x, y R

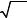– мнимая единица i2 = −1

х=Re z – действительная часть комплексного числа, y=Im z – мнимая часть.

Ох – действительная ось, Оy – мнимая ось. z = x + yi z = x − yi – сопряжённое число.

Рисунок 42

Модуль, аргумент

Модуль: z = r = x2 + y2

Рисунок 43

53

Деление: умножаем числитель и знаменатель на комплексное число, сопряжённое к знаме-

нателю:

Возведение в степень (n ):

zn = ( x + yi)n = ( x + yi )×( x + yi )×...×( x + yi)

n раз

или : zn = (r (cosϕ + i sinϕ ))n = r n (cos nϕ + i sin nϕ ) - формула Муавра.

54

ЗАДАЧИ Для аудиторной работы

170. Изобразить комплексные числа на плоскости, найти их модуль и аргу-

мент: z1 = 5 + 4i; z2 = −3 − 3i; z3 = 2i; z4 = −5 .

171. Решить уравнение:

а) x2 − 2x + 2 = 0, б) x2 + 25 = 0,

в) x3 + 8 = 0,

г) x4 −16 = 0.

172.Выполнить действия:

а) (4 + 2i) − 3(1− i),

б) (2 + 3i)(3 − 2i), в) (3 − 2i)2 ,

г) 1+ 2i , 2 + 3i

д) (2 + i)(2 − i) . 4 − 3i

173. Записать комплексные числа в тригонометрической и показательной

форме: z1 = 1; z2 = 1+ i; z3 = −3 + 3 i; z4 = 6i .

174.Найти: i10 ,i−24 ,i7 ,(1+ i)10 ,(1− 3i)6 .

175.Построить на комплексной плоскости множество точек, удовлетворяющих условию:

а) z = 2,

б)2 < z ≤ 5,

в) arg z = − π , 3

г) z > 3, arg z = 3π , 4

е) z − 2 = 3.

55

Задачи для самостоятельной работы

176. Изобразить комплексные числа на плоскости, найти их модуль и аргу-

мент: z1 = −2 + 4i; z2 = −3i; z3 = 4 − 4i .

177. Решить уравнение:

178. Выполнить действия:

179. Записать комплексные числа в тригонометрической и показательной

форме: z1 = −1; z2 = 3 + 3i; z3 = −1− 3i.

180. Построить на комплексной плоскости множество точек, удовлетворяющих условию:

Вопросы для самоконтроля по главе 6 «Комплексные числа»

1.Что называется комплексным числом?

2.Что такое мнимая единица?

3.Что называется действительной частью комплексного числа, мнимой частью?

4.Что такое модуль комплексного числа, как его вычислить?

5.Что такое аргумент комплексного числа, как его найти?

6.Как выполняются действия сложения, вычитания, умножения на число для комплексных чисел?

7.Как перемножить два комплексных числа?

8.Как возвести комплексное число в степень?

9.Напишите тригонометрическую и показательную форму записи комплексного числа.

56

ПРИЛОЖЕНИЯ

Приложение А

Итоговые тесты

Тест 1

1)2,4;

2)0;

3)-2,4;

4)1.

обратной к матрице А при λ, равном …

1)3;

2)1;

3)4;

4)2.

3x + 2 y − z = 1,

Задание № 7. Дана система линейных уравнений: − + λ =

x y z 0,2x − 2 y + 3z = 0.

Эту систему нельзя решить методом Крамера при λ, равном …

1)0;

2)3;

3)1;

4)1,5.

58

2)(1;–2;4);

3)(1;10;0);

4)(1;7;2).

Задание № 12. Даны координаты вершин треугольника: А(–5;3), В(1;6) и С(7;–2). Тогда длина медианы АМ равна …

1)82;

2)85 ;

3)82 ;

4)5 .

Задание № 13. Даны вершины треугольника: А(3;-1), В(0;4), С(-4;-2). Тогда площадь треугольника равна ____.

Задание № 14. Точка А(−3; 3) задана в прямоугольной системе координат. То-

гда её полярные координаты равны …

1) r = 23,ϕ = − π ; 6

2) r = 23,ϕ = π ; 6

3)r = 5π ,ϕ = 23 ; 6

4)r = 23,ϕ = 5π .

6

Задание № 15. Дано уравнение прямой в общем виде 3x − 5 y −15 = 0 . Тогда урав-

нение этой прямой в отрезках имеет вид …

1)x − y = 1; 3 5

2)x + y = 1; 5 −3

3)x − y = 0; 5 3

60