
- •1. Лабораторная работа №1. МЕТОДЫ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- •1.1. Погрешности приближенных вычислений
- •1.1.1. Правила оценки погрешностей
- •1.1.2. Оценка ошибок при вычислении функций
- •1.1.3. Правила подсчета цифр
- •1.1.4. Вычисления со строгим учетом предельных абсолютных погрешностей
- •1.1.5. Вычисления по методу границ
- •1.2. Пример выполнения лабораторной работы
- •1.2.1. Задание к лабораторной работе
- •1.2.2. Решение типового примера
- •1.2.3. Варианты заданий
- •2. Лабораторная работа №2. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •2.1. Прямые методы решения
- •2.1.1. Постановка задачи
- •2.1.2. Метод Гаусса
- •2.1.3. Оценки погрешностей решения системы
- •2.2. Итерационные методы решения
- •2.2.1. Метод простой итерации (МПИ)
- •2.2.2. Метод Якоби
- •2.2.3. Метод Зейделя
- •2.2.4. Метод релаксации
- •2.3. Пример выполнения лабораторной работы
- •2.3.1. Задание к лабораторной работе
- •2.3.2. Решение типового примера
- •2.3.3. Варианты заданий
- •3. Лабораторная работа №3. РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •3.1. Численные методы решения нелинейных уравнений
- •3.1.1. Локализация корней
- •3.1.2. Метод Ньютона
- •3.1.3. Модификации метода Ньютона
- •3.1.4. Метод Стеффенсена
- •3.1.5. Метод секущих
- •3.1.6. Задача «лоцмана»
- •3.1.7. Метод хорд
- •3.1.8. Метод простой итерации
- •3.2. Пример выполнения лабораторной работы
- •3.2.1. Задание к лабораторной работе
- •3.2.2. Решение типового примера
- •3.2.3. Варианты заданий
- •4. Лабораторная работа №4. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- •4.1. Численные методы решения систем нелинейных уравнений
- •4.1.1. Метод Ньютона
- •4.1.2. Метод простой итерации
- •4.1.3. Метод наискорейшего спуска
- •4.2. Пример выполнения лабораторной работы
- •4.2.1. Задание к лабораторной работе
- •4.2.2. Решение типового примера
- •4.2.3. Варианты заданий
- •5. Лабораторная работа №5. ИНТЕРПОЛЯЦИЯ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ
- •5.1. Интерполяция таблично заданных функций
- •5.1.1. Интерполяционный многочлен Лагранжа
- •5.1.2. Полином Ньютона
- •5.1.3. Кусочно-линейная и кусочно-квадратичная аппроксимация
- •5.2. Пример выполнения лабораторной работы
- •5.2.1. Задание к лабораторной работе
- •5.2.2. Решение типового примера
- •5.2.3. Варианты заданий
- •6. Лабораторная работа №6. АППРОКСИМАЦИЯ ФУНКЦИИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
- •6.1. Метод наименьших квадратов
- •6.2. Пример выполнения лабораторной работы
- •6.2.1. Задание к лабораторной работе
- •6.2.2. Решение типового примера
- •6.2.3. Варианты заданий
- •7. Лабораторная работа №7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •7.1. Численное интегрирование
- •7.1.1. Задача численного интегрирования
- •7.1.1. Квадратурная формула прямоугольников
- •7.1.2. Квадратурные формулы Ньютона – Котеса
- •7.1.3. Квадратурные формулы трапеций и Симпсона
- •7.1.4. Правило Рунге
- •7.2. Пример выполнения лабораторной работы
- •7.2.1. Задание к лабораторной работе
- •7.2.2. Решение типового примера
- •7.2.3. Варианты заданий
- •8. Лабораторная работа №8. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •8.1. Численные методы решения обыкновенных дифференциальных уравнений
- •8.1.1. Постановка задачи
- •8.1.2. Метод Эйлера
- •8.1.4. Выбор шага интегрирования
- •8.1.5. Многошаговые методы Адамса
- •8.2. Пример выполнения лабораторной работы
- •8.2.1. Задание к лабораторной работе
- •8.2.2. Решение типового примера
- •8.2.3. Варианты заданий
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
3. Лабораторная работа №3. РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
3.1. Численные методы решения нелинейных уравнений
3.1.1. Локализация корней
Будем рассматривать задачу приближенного нахождения нулей
функции одной переменной |
|
f (x) = 0 , |
(3.1) |
где f : R1 ® R1 – алгебраическая или трансцендентная функция. |
|
Теорема 1 (Больцано–Коши). Если |
непрерывная на[a, b] |
функция f(x) на концах его имеет противоположные знаки, т. е. |
|
f (a) × f (b) < 0 , |
(3.2) |
то на интервале (a, b) она хотя бы один раз обращается в ноль.
Слабость теоремы:
1.Не дает ответа на вопрос о количестве корней на [a, b] в случае выполнения условия (3.2).
2.Если условие (3.2) не выполнено, то не позволяет утверждать, что корней на [a, b] нет.
Усиление теоремы. |
|
|
|
|
|
|
|
|
||
Теорема 2. Непрерывная, строго монотонная функция f(x) |
имеет |
|
|
|||||||
и при том единственный ноль на отрезке[a, b] тогда и только тогда, |
|
|
||||||||
когда на его концах она принимает значения разных знаков. |
|
|
|
|||||||
Установить |
монотонность |
на |
данном |
отрезке |
можно |
для |
||||
дифференцируемой |
|
функции, |
|
потребовав |
знакопостоянства |
ее |
|
|||
производной на всем отрезке. |
|
|
|
|
|
|
|
|
||
Теорема 3. Пусть |
f ÎC1[a;b] |
, |
тогда если f ' (x) |
не меняет знак на |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
интервале (a, b), |
то |
условие (3.2) |
является |
необходимым |
и |
|
||||
достаточным для того, чтобы уравнение (3.1) имело и при этом |
|
|
||||||||
единственный корень на отрезке [a, b]. |
|
|
|
|
|
|
||||
45
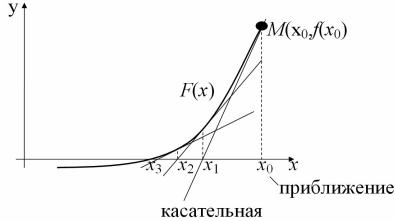
3.1.2. Метод Ньютона
Рассмотрим f (x) = 0 и построим итерационный процесс:
xn+1 = xn - |
f (xn ) |
, n = 0,1,2,... |
|
(3.3) |
|
|
|
|
|||
|
f `(xn ) |
|
|
|
|
Запишем |
|
уравнение |
касательной |
в x0 : |
точке |
y - f (x0 ) = f `(x0 )(x -x0 ) .
Найдем точку пересечения касательной с осью абсцисс:
y = 0 , тогда |
x |
» x |
|
- |
f (x0 ) |
. |
0 |
|
|||||
|
1 |
|
|
f `(x0 ) |
||
|
|
|
|
|
||
Затем проводим касательную в x1 и находим x2 и так далее.
Поэтому метод Ньютона так же называют методом касательных.
Рис. 3.1. Метод Ньютона (касательных)
Необходимые условия сходимости метода Ньютона:
1. |
Функция f(x) |
должна |
быть |
|
дважды дифференцируема и |
||||||||
непрерывна, должна |
иметь |
непрерывную первую производную, а |
|||||||||||
|
f '' (x) |
|
< M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
f ' (x) ¹ 0 |
на |
всем |
|
промежутке, содержащем |
корень |
|||||||
"x Î[a,b] : x* Î[a,b] . |
|
|
|
|
|
|
|
|
|||||
3. |
f '' (x) |
сохраняет |
знак |
[a,b] |
, |
f |
'' (x) < 0 |
– функция |
выпукла |
||||
|
на |
|
|
||||||||||
вверх, |
f '' (x) > 0 – функция выпукла вниз. |
|
|
|
|||||||||
46

4. Начальное приближение x0 : f (x0 ) f '' (x0 ) > 0 .
Теорема. При выполнении необходимых условий1–4,
итерационный процесс Ньютона(3.3) сходится к решениюx* уравнения (3.1) с квадратичной скоростью в окрестности корня x* .
3.1.3.Модификации метода Ньютона
I.Разностный метод с постоянным шагом.
Пусть |
для |
|
|
|
построен итерационный |
процесс метода |
||||
Ньютона |
|
|
|
|
|
|
|
|
|
|
xn+1 = xn |
- |
f (xn ) |
|
, n = 0,1,2,... |
|
(3.4) |
||||
|
|
|
|
|||||||
|
|
f `(xn ) |
|
|
|
|
||||
Для сложных функций вычисление f ' (x) достаточно трудоемко, |
||||||||||
поэтому заменим в (3.4) производную по определению |
|
|||||||||
f `(xn ) = lim |
f (xn + h) - f (xn ) |
. |
|
|||||||
|
|
|
h |
|
|
|
||||
|
h®0 |
|
|
|
|
|
||||
При малых значениях шага h получим приближенное равенство |
||||||||||
xn+1 = xn |
- |
|
|
f |
(xn ) × h |
|
. |
|
(3.5) |
|
f (xn |
|
|
|
|
|
|||||
|
|
+ h) - f (xn ) |
|
|
||||||
II. Разностный метод с переменным шагом.
Шаг h можно изменять на каждой итерации либо проводить
несколько |
итераций с |
одним |
шагом, затем его изменить(в |
|||
зависимости от свойств функции). Тогда получим набор h1 , h2 ,... |
||||||
Тогда (3.5) примет вид |
|
|
||||
xn+1 = xn |
- |
|
f (xn ) × hk |
, n ¹ k . |
(3.6) |
|
f (xn |
+ hk ) - f (xn ) |
|||||
|
|
|
|
|||
Преимуществом методов этой группы является отсутствие производной. Недостатком – низкая скорость сходимости.
47

3.1.4. Метод Стеффенсена
Если учесть, что функция f (xn ) ® 0 с той же скоростью, что и
xn ® x* , то есть смысл полагать, что hk |
= f (xn ) . Это можно сделать на |
|||||||||||
той стадии итерационного процесса, когда значения функции |
|
f (xn ) |
|
|
||||||||
|
|
|||||||||||
уже |
достаточно |
малы. При таких hk |
итерационный процесс |
|||||||||
принимает вид: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
[f (xn )]2 |
|
|
|
|
|
|
||
|
xn+1 |
= xn - |
|
|
|
. |
|
(3.7) |
||||
|
|
|
|
|
||||||||
|
|
|
f (xn + f (xn )) - f (xn ) |
|
|
|
|
|
|
|||
|
Метод имеет сугубо локальный характер сходимости, но зато |
|||||||||||
сходимость квадратичная. |
|
|
|
|
|
|
||||||
|
|
|
|
3.1.5. Метод секущих |
||||||||
|
Пусть в (3.6) hk |
= xn-1 - xn , тогда xn-1 |
= xn |
+ hk . |
||||||||
|
xn+1 |
= xn - |
f (xn ) × (xn-1 - xn ) |
, |
|
(3.8) |
||||||
|
|
|
||||||||||
|
|
|
f (xn-1 ) - f (xn ) |
|
|
|
|
|
|
|||
где x0 и x1 задаются.
Формула (3.8) определяет новый метод как двухшаговый.
Рис. 3.2. Метод секущих
Из геометрических соображений легко понять, что xn+1 есть абсцисса точки пересечения с осью хОпрямой, проведенной через точки ( xn-1 ; f (xn-1 ) ) и ( xn ; f (xn ) ), т. е. секущей.
48
