
- •1. Лабораторная работа №1. МЕТОДЫ ОЦЕНКИ ПОГРЕШНОСТЕЙ
- •1.1. Погрешности приближенных вычислений
- •1.1.1. Правила оценки погрешностей
- •1.1.2. Оценка ошибок при вычислении функций
- •1.1.3. Правила подсчета цифр
- •1.1.4. Вычисления со строгим учетом предельных абсолютных погрешностей
- •1.1.5. Вычисления по методу границ
- •1.2. Пример выполнения лабораторной работы
- •1.2.1. Задание к лабораторной работе
- •1.2.2. Решение типового примера
- •1.2.3. Варианты заданий
- •2. Лабораторная работа №2. МЕТОДЫ РЕШЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •2.1. Прямые методы решения
- •2.1.1. Постановка задачи
- •2.1.2. Метод Гаусса
- •2.1.3. Оценки погрешностей решения системы
- •2.2. Итерационные методы решения
- •2.2.1. Метод простой итерации (МПИ)
- •2.2.2. Метод Якоби
- •2.2.3. Метод Зейделя
- •2.2.4. Метод релаксации
- •2.3. Пример выполнения лабораторной работы
- •2.3.1. Задание к лабораторной работе
- •2.3.2. Решение типового примера
- •2.3.3. Варианты заданий
- •3. Лабораторная работа №3. РЕШЕНИЕ НЕЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
- •3.1. Численные методы решения нелинейных уравнений
- •3.1.1. Локализация корней
- •3.1.2. Метод Ньютона
- •3.1.3. Модификации метода Ньютона
- •3.1.4. Метод Стеффенсена
- •3.1.5. Метод секущих
- •3.1.6. Задача «лоцмана»
- •3.1.7. Метод хорд
- •3.1.8. Метод простой итерации
- •3.2. Пример выполнения лабораторной работы
- •3.2.1. Задание к лабораторной работе
- •3.2.2. Решение типового примера
- •3.2.3. Варианты заданий
- •4. Лабораторная работа №4. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
- •4.1. Численные методы решения систем нелинейных уравнений
- •4.1.1. Метод Ньютона
- •4.1.2. Метод простой итерации
- •4.1.3. Метод наискорейшего спуска
- •4.2. Пример выполнения лабораторной работы
- •4.2.1. Задание к лабораторной работе
- •4.2.2. Решение типового примера
- •4.2.3. Варианты заданий
- •5. Лабораторная работа №5. ИНТЕРПОЛЯЦИЯ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ
- •5.1. Интерполяция таблично заданных функций
- •5.1.1. Интерполяционный многочлен Лагранжа
- •5.1.2. Полином Ньютона
- •5.1.3. Кусочно-линейная и кусочно-квадратичная аппроксимация
- •5.2. Пример выполнения лабораторной работы
- •5.2.1. Задание к лабораторной работе
- •5.2.2. Решение типового примера
- •5.2.3. Варианты заданий
- •6. Лабораторная работа №6. АППРОКСИМАЦИЯ ФУНКЦИИ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
- •6.1. Метод наименьших квадратов
- •6.2. Пример выполнения лабораторной работы
- •6.2.1. Задание к лабораторной работе
- •6.2.2. Решение типового примера
- •6.2.3. Варианты заданий
- •7. Лабораторная работа №7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
- •7.1. Численное интегрирование
- •7.1.1. Задача численного интегрирования
- •7.1.1. Квадратурная формула прямоугольников
- •7.1.2. Квадратурные формулы Ньютона – Котеса
- •7.1.3. Квадратурные формулы трапеций и Симпсона
- •7.1.4. Правило Рунге
- •7.2. Пример выполнения лабораторной работы
- •7.2.1. Задание к лабораторной работе
- •7.2.2. Решение типового примера
- •7.2.3. Варианты заданий
- •8. Лабораторная работа №8. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- •8.1. Численные методы решения обыкновенных дифференциальных уравнений
- •8.1.1. Постановка задачи
- •8.1.2. Метод Эйлера
- •8.1.4. Выбор шага интегрирования
- •8.1.5. Многошаговые методы Адамса
- •8.2. Пример выполнения лабораторной работы
- •8.2.1. Задание к лабораторной работе
- •8.2.2. Решение типового примера
- •8.2.3. Варианты заданий
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
7. Лабораторная работа №7. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
7.1.Численное интегрирование
7.1.1.Задача численного интегрирования
Пусть на отрезке[a,b] задана функция f (x) . Найти значение
b
интеграла ò f (x)dx . Для некоторых функций трудно найти интеграл.
a
Определение. Выражение ågi fi , где gi Î R , fi = f (xi ) называется
i
квадратурной формулой.
Таким образом, задача сводится к представлению интеграла с
b
помощью квадратурной формулы: ò f (x)dx =ågi fi на отрезке [a,b].
a i
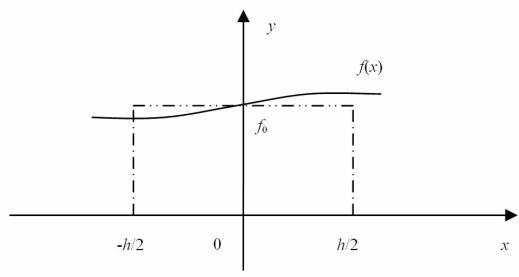
7.1.1. Квадратурная формула прямоугольников
Рис. 7.1. График функции
Как видно, из рис. 7.1 интеграл можно вычислить как
h / 2
òf (x)dx » hf0 .
-h / 2
90
x
Обозначим интеграл F(x) = ò f (x)dx .
0
Тогда по формуле Лейбница можно записать
h / 2
ò f (x)dx » F(h / 2) - F(-h / 2) .
-h / 2
По формуле Тейлора
F (±h / 2) = F (0) ± |
h |
|
¢ |
|
|
|
+ |
|
h 2 |
1 |
|
¢¢ |
|
|
h3 |
1 |
|
|
|
|
|
|
¢¢¢ |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
F (0) |
|
|
4 |
2! |
F (0) ± |
8 |
|
|
3! |
F (0) + ... = |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
||||||||||||||
|
|
h |
|
|
|
|
h2 |
|
1 |
|
|
|
¢ |
|
|
|
|
h3 |
|
|
1 |
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= ± |
|
|
f (0) + |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
4 |
|
2! |
|
(0) ± |
|
|
|
8 |
|
|
3! |
f (0) + ... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
h / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h3 |
|
|
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
ò f (x)dx = F (h / 2) - F (-h / 2) = hf (0) + |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
24 |
|
(0) . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
-h / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким |
|
|
|
|
|
|
образом, |
|
|
локальное |
|
|
|
|
|
|
|
|
|
|
|
представление |
формулы |
|||||||||||||||||||||||||||||
прямоугольников |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
h / 2 |
|
|
|
|
|
|
|
|
|
æ |
|
h |
3 |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ò f (x)dx = hf (0) + Î |
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.1) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ç |
|
|
|
|
|
÷ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
-h / 2 |
|
|
|
|
|
|
|
|
|
è 24 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть отрезок [a,b] разбит на n частей, тогда |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
h |
3 |
n |
|
|
|
||||||
ò f (x)dx » å(hf (xi-1 ) + |
|
|
|
|
f ¢¢(x)) = åhf (xi-1 ) + |
|
å f ¢¢(x ) = |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
24 i=1 |
. |
|
|
|||||||||||
|
|
n |
|
|
|
|
|
h |
3 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
b - a |
n |
|
|
|
|
|
|
|
h |
2 |
|
|
b |
- a |
|
|
|
|||||||||
= hå f (xi |
-1 ) + |
|
|
|
f ¢¢(x)å1 = |
å f (xi-1 ) + |
|
|
|
|
f ¢¢(x)n |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
i=1 |
|
|
|
|
24 |
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
n |
i=1 |
|
|
|
|
|
|
|
24 n |
|
|
|
|||||||||||||||||||
Таким |
образом, |
|
если |
|
|
|
|
|
f ÎC[2a,b ,] |
x Î[a,b], |
|
получаем |
глобальную |
|||||||||||||||||||||||||||||||||||||||
формулу прямоугольников |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
b |
|
|
b |
- a |
n |
|
|
|
|
|
|
|
|
|
|
b - a |
|
|
2 |
|
|
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ò f (x)dx @ |
|
|
å f (xi-1 ) + |
|
|
|
|
|
|
h |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.2) |
||||||||||||||||
|
n |
24 |
|
|
|
|
|
|
|
|
(x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
a |
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
7.1.2. Квадратурные формулы Ньютона – Котеса |
|
|||||||||||||||||||||||||||||||||||||||||||||||
Идея: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
подставляют |
|||||
в |
|
|
|
|
интеграл ò f (x)dx |
|
|
|
|
вместо f (x) |
|
|||||||||||||||||||||||||||||||||||||||||
a
интерполяционный полином Лагранжа.
91
Функция |
f (x) ÎC[na+,b1 |
] |
|
|
|
может |
быть |
единственным |
образом |
|||||||||||
представлена в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
f (x) = Ln (x) + Rn (x) , |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
n |
|
|
, pi |
|
|
|
|
|
|
|
|
|
|
|
|
|||
где Ln (x) = å pi (x) fi |
|
(x) |
|
– базисные многочлены, |
|
|||||||||||||||
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Rn (x) = |
f (n+1) |
(x) |
Wn (x) – |
|
отклонение, |
|
|
|
|
|||||||||||
(n + |
1)! |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Wn (x) = (x - x0 )(x - x1 )...(x - xn ) . |
|
|
|
|
||||||||||||||||
Пусть |
|
последовательность {xi }in=0 совпадает |
с точками разбиения |
|||||||||||||||||
отрезка [a,b] с шагом h |
|
xk |
|
= x0 |
+ kh , тогда |
|
|
|||||||||||||
|
|
|
|
n |
|
|
(-1) |
n-i |
|
|
|
k(k -1)...(k - n) |
|
|
|
|||||
Ln (x0 + kh) = å |
|
|
|
|
|
fi . |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
i=0 |
|
i!(n - i)! |
k -i |
|
|
|
|
|||||||||
Изменим границы интегрирования: |
x = a ® k = 0; x = b ® k = n ; |
|||||||||||||||||||
dx = hdk , получим квадратурную формулу Ньютона – Котеса |
|
|||||||||||||||||||
b |
|
n n |
(-1) |
n-i |
k(k |
-1)...(k - n) |
|
|
|
|
|
|||||||||
ò f (x)dx @ hòå |
|
|
|
fi dk . |
|
(7.3) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
a |
|
0 i=0 i!(n - i)! |
|
|
|
|
|
k - i |
|
|
|
|
||||||||
7.1.3. Квадратурные формулы трапеций и Симпсона
Формула трапеций и Симпсона являются частными случаями
формулы Ньютона – Котеса. |
|
|
|
|
|
|
|
|
|
|
|||||||||
Применим |
|
полином |
|
Ньютона(эквивалентный |
|
многочлену |
|||||||||||||
Лагранжа в силу единственности): |
|
|
|
|
|
|
|
||||||||||||
P (x |
|
+ kh) = y |
|
+ kDy |
|
+ |
k (k -1) |
D2 y |
|
+ ... + |
k (k -1)...(k - n +1) |
Dn y |
. |
||||||
0 |
0 |
0 |
|
0 |
|
||||||||||||||
n |
|
|
|
|
|
|
2! |
|
|
|
|
n! |
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I. Формула трапеций |
|
|
|
|
|
|
|
|
|
|
|||||||||
Пусть |
n = 1, т. е. |
имеем две точки x0 и |
x1 = x0 + h , и известны |
||||||||||||||||
значения |
|
функции y0 |
= f (x0 ), y1 |
= f (x1 ) . Этим |
точкам |
соответствуют |
|||||||||||||
k = 0, k = 1 , |
тогда |
получим |
простейшую |
квадратурную формулу |
|||||||||||||||
трапеций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92
|
x1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
é |
|
|
|
k 2 |
|
ù1 |
|
æ |
|
|
|
|
y - y |
0 |
|
ö |
|
|
||||||||
|
ò f (x)dx »ò( y0 |
|
+ kDy0 )hdk = hêy0k + |
|
Dy0 ú |
|
= hç y0 + |
1 |
|
|
÷ |
= |
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
x0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
û0 |
|
è |
|
|
|
|
|
|
|
|
ø |
, |
(7.4) |
|||||||
|
|
y0 + y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= |
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где h = |
b - a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Остаточный член формулы трапеций r1 = - |
f ¢¢(x1 ) |
h3 ,x1 Î(x0 , x1 ). |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
||
II. Формула Симпсона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Пусть n = 2 , |
т. е. интерполируем функцию f (x) по трем точкам |
|||||||||||||||||||||||||||||||||||||||||||
x0 , x1 = x0 |
+ h , |
|
x2 |
= x0 + 2h , тогда |
|
получим |
|
простейшую |
формулу |
|||||||||||||||||||||||||||||||||||
Симпсона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x2 |
|
|
|
|
2 |
|
é |
|
|
|
|
|
|
|
|
k(k -1) |
|
2 |
|
ù |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ò f (x)dx » ò |
|
êy0 |
+ kDy0 |
+ |
|
|
|
D y0 |
úhdk |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
x0 |
|
|
|
|
0 |
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(7.5) |
||||||
|
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ù |
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
= hê2 y0 + 2( y1 - y0 ) + |
|
|
(y2 - 2 y1 |
+ y0 )ú |
= |
|
|
( y0 |
+ 4 y1 + y2 ) |
|
|
|
|||||||||||||||||||||||||||||||
|
3 |
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Остаточный член формулы Симпсона r2 |
|
= - |
h5 |
|
f IV (x ),x Î(x0 , x2 ). |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
Для |
применения |
|
|
простейшей |
|
формулы |
|
|
Симпсона интервал |
|||||||||||||||||||||||||||||||||||
должен быть симметричен относительно точки x1 : (x1 |
- h; x1 |
+ h) . |
|
|||||||||||||||||||||||||||||||||||||||||
Распространим формулы трапеций и Симпсона на все отрезки |
||||||||||||||||||||||||||||||||||||||||||||
разбиения [a,b]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Глобальная формула трапеций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
yn |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.6) |
|||||
|
ò f (x)dx =h( |
|
+ y1 + y2 |
|
+ ... + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Оценка погрешности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
| Rn |£ M |
| b - a | h2 |
|
|
|
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.7) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
12 |
|
, M = max | f (x) |; x Î[a, b .] |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Глобальная формула Симпсона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
b |
|
|
|
|
|
2h |
|
y0 + y2m |
+ 2 y1 + y2 +... + 2 y2m-1 ) . |
|
|
|
|
|
|
|
|
|
|
|
(7.8) |
||||||||||||||||||||||
|
ò f (x)dx = |
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
93
