Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Chumakin

.pdf

Скачиваний:

Добавлен:

23.03.2016

Размер:

357.17 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Министерство образования Российской Федерации

Ульяновский государственный технический университет

ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ.

РЯДЫ ФУРЬЕ.

Ульяновск 2003

УДК 517(076)

ББК 2.193 я 7

Ч-67

Рецензент канд.физ.-мат.наук, доцент Ш. Т. Ишмухаметов

Одобрено секцией методических пособий научнометодического совета университета

Числовые и функциональные ряды. Ряды Фурье: Методические указания к типовому расчету по высшей математике / Сост.: М. Е. Чумакин, Г. Д. Павленко.─ Ульяновск:УлГТУ, 2003.─ 39с.

Работа подготовлена на кафедре «Высшая математика» Настоящие методические указания составлены в соответствии с программами курса

высшей математики для студентов младших курсов всех специальностей УлГТУ.

Изложена методика выполнения типового расчета по числовым и функциональным рядам и рядам Фурье, даны образцы решения задач с предварительным теоретическим обоснованием.

УДК 517(076)

ББК 2.193 я 7

ОГЛАВЛЕНИЕ
1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ………………………………	4
2. ЧИСЛОВЫЕ РЯДЫ…...………………………………………………	4
2.1. Указания к задаче 1………………………………………...	4
2.2. Указания к задаче 2……………………………………….	5
1.3. Указания к задаче 3……………………………………….	6
2.4. Указания к задаче 4……………………………………….	8
2.5. Указания к задаче 5…………………………………………	9
2.6. Указания к задаче 6…………………………………………	9
2.7. Указания к задаче 7…………………………………………	10
2.8. Указания к задаче 8…………………………………………	11
2.9. Указания к задаче 9 ………………………………………..	12
2.10. Указания к задаче 10……………………………………….	13
3. ФУНКЦИОНАЛЬНЫЕ РЯДЫ……...………………………………….	14
3.1. Указания к задаче 11………………………………………	14

3.2.Указания к задаче 12……………………………………….. 16

3.3.Указания к задаче 13……………………………………….. 18

3.4.Указания к задаче 14……………………………………….. 18

3.5.Указания к задаче 15……………………………………….. 18

3.6.Указания к задаче 16……………………………………….. 19

3.7.Указания к задаче 17……………………………………….. 20

3.8.Указания к задаче 18………………………………………. 23

3.9.Указания к задаче 19………………………………………. 24

3.10. Указания к задаче 20………………………………………	26
4. РЯДЫ ФУРЬЕ……...……………………………………………………	26
4.1. Указания к задаче 21………………………………………	30
4.2. Указания к задаче 22………………………………………	35
БИБЛИОГРАФИЧЕСКИЙ СПИСОК...…………………………………	39

1. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

В целях лучшего усвоения курса математики и интенсификации самостоятельных занятий студентов в программах по высшей математике предусмотрено выполнение типовых расчетов. Каждый типовой расчет должен быть заданием по целому разделу курса и состоять из теоретических вопросов, теоретических упражнений, задач и примеров. Теоретические вопросы и теоретические упражнения должны быть общими для всех студентов, примеры и задачи ─ индивидуальными.

Предлагаемые методические указания являются руководством для выполнения типового расчета по теме «Ряды» из учебного пособия Л. А. Кузнецова «Сборник заданий по высшей математике (типовые расчеты)», который удовлетворяет вышеуказанным требованиям программы к типовым расчетам. В связи с отсутствием в указанном сборнике Л. А. Кузнецова рядов Фурье в данное пособие включены задания по рядам Фурье.

Сначала предлагается найти ответы на теоретические вопросы в учебниках [1-3] и в конспектах лекций, а затем выполнять теоретические упражнения и решать задачи и примеры. Выполнение теоретических упражнений и решение задач и примеров помогут приобрести студентам первоначальные навыки в научно-исследовательской работе по математике и в решении прикладных задач.

Все примеры указаний имеют двойную нумерацию. Например, номера 1.1 и 1.2 означают, что они даны к задаче 1 сборника Л. А. Кузнецова, примеры 2.1 и 2.2 даны к задаче 2 и т.д.

2. ЧИСЛОВЫЕ РЯДЫ

2.1.Указания к задаче 1

Пусть а1 , a2 ,..., an ,..., ─ заданная числовая последовательность. Выражение

a1 + a2	∞
a1 + a2	+ ... + an + ... = ∑ an	(1.1)
	n=1
называется числовым рядом. Конечные суммы
S1 = a1 , S2 = a1 + a2 ,...,	Sn = a1 + a2 + ... + an ,...	(1.2)

называются частичными суммами ряда (1.1).

Если существует конечный предел последовательности частичных сумм

(1.2) S = lim Sn , то ряд (1.1) называется сходящимся, а число S ─ суммой ряда

n → ∞

(1.1).

Если ряд (1.1) сходится, то lim an = 0 (необходимый признак сходимости).

n→∞

Пример 1.1. Найти сумму ряда

∞

∑

(1.3)

49n

− 70n −

n=1

Решение. Сначала решим уравнение

49x2

− 70x − 24 = 0.

Корнями этого уравнения являются числа

= −

и x

, следовательно,

= (7x

+ 2)(7x −12).

49x

− 70x − 24 =

49 x

x −

Теперь

методом

неопределенных

коэффициентов

выражение

разложим на простейшие дроби:

49x 2

− 70x − 24

откуда

49x 2 − 70x − 24

(7x + 2)(7x −12)

7x + 2

7x −12

A(7x − 12) + B(7x + 2) = 14 .

x ,

Приравнивая коэффициенты при одинаковых степенях

получаем систему

уравнений:

7 A + 7B = 0,

− 12A + 2B = 14,

из которой находим: А=-1 и В=1, следовательно,

−

(1.4)

−12

7x +

49x 2 − 70x − 24

Учитывая (1.4), частичную сумму ряда (1.3) можно записать следующим

образом:

∑

−

= −

−

2 −

−

7k − 12

7k + 2

k 1

70k

= 49k

−

+ ... +

−

7(n − 2) − 12

7(n − 2) + 2

7(n − 1) − 12

7(n − 1) + 2

−

= −

−

7n − 12

7n + 2

7(n − 1) + 2

7n + 2

7n − 5

7n + 2

следовательно,

lim S

lim

−

= 0,3.

7n − 5

n→∞

n → ∞

Значит, ряд (1.3) сходится и его сумма S = 0,3.

2.2 Указания к задаче 2 Задача 2 решается аналогично задаче 1.

Пример 2.1. Найти сумму ряда

∞	3n	+ 8
∑n=1			(2.1)
	n(n +1)(n + 2)

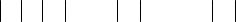
Решение. Методом неопределенных коэффициентов общий член ряда (2.1) разложим на простейшие дроби

3n + 8

−

= 4

−

n(n +1)(n +

n +1

n + 2

n +1

n + 2

n +1

Тогда частичную сумму ряда (2.1) можно записать в виде

3k + 8

Sn = ∑

= 4∑

−

∑

−

+ 1)(k +

+ 1

k =1 k

k + 1

k =1 k

k + 2

= 4 1−

−

+ ... +

−

n +

−

+ ... +

−

= 4 1−

−

n +1

n +

n +1

n + 2

= 3,5 −

n +1

n + 2

значит,

lim

3,5

−

= 3,5

n + 1

n +

n → ∞

следовательно, ряд (2.1) сходится и имеет сумму S = 3,5.

2.3 Указания к задаче 3

Ряд

∞

a1 + a2 + ... + an + ... = ∑ an (3.1)

n=1

называют абсолютно сходящимся, если сходится ряд

∞

a1 + a2 + ... + an + ... = ∑ an . (3.2)

n=1

Если ряд (3.1) сходится, а ряд (3.2) расходится, то ряд (3.1) называется условно

сходящимся.

Если члены	ряда (3.1)	для всех номеров n , начиная с		некоторого,
				∞
удовлетворяют	условию	an	≤ bn , причем знакоположительный	ряд ∑bn
				n=1

сходится, то ряд (3.1) сходится абсолютно. Если для всех номеров n , начиная с некоторого, члены ряда (3.1) удовлетворяют условию 0 < cn ≤ an , причем ряд

∞

∑ cn расходится, то ряд (3.1) также расходится (признак сравнения).

n = 1

∞

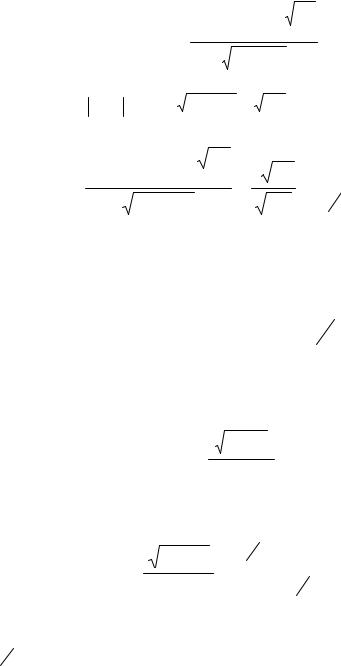
Если ряд ∑ dn сходится абсолютно и существует конечный предел

n = 1

= q < +∞ , то ряд (3.1) сходится абсолютно. Если члены рядов

∞

lim

∑ a

n → ∞

n = 1

∞

положительны и 0 <

< +∞ ,

то эти ряды либо оба сходятся,

либо

∑ b

lim

n = 1

n → ∞ bn

оба расходятся (предельный признак сравнения).

Пример 3.1. Исследовать на сходимость ряд

nπ 3

∞

+ 2 cos

(3.3)

∑

n = 1

+10

Решение. Так как cos x ≤ 1,

n11 +10 > 6 n11 , то

+ 2 cos

nπ

< 53 n2

0 <

(3.4)

7 6

6 n11 + 10

6 n11

Обобщенный гармонический ряд (ряд Дирихле)

и расходится при α ≤ 1. Следовательно, ряд	∞	5
	∑
		7 6
	n = 1 n

соотношения (3.4), ряд (3.3) также сходится.

Пример 3.2. Исследовать на сходимость ряд

∞	n	3	+ 2
∑
n = 1 n	2 sin 2 n

Решение. Так как

n3 + 2	>	n 3	2	=	1
n2 sin 2 n		n2			n	12

∞	1	сходится при α > 1
∑

n = 1 nα

сходится. Поэтому, в силу

(3.5)

∞	1
и ряд ∑				расходится , то ряд (3.5) также расходится.
		1
n =1n			2

Пример 3.3. Исследовать на сходимость ряд

∞		n	2	− 3
∑ arctg
n=2	n 2	− 4n

∞ 1

Решение. Гармонический ряд n∑=1 n расходится и

n2 − 3

lim

arctg

lim

− 3

arctg n

− 4n

n → ∞

(3.6)

n	=	π
n	=	π	,
		2
n2 − 4n

следовательно, ряд (3.6) расходится.

2.4. Указания к задаче 4

Задачу 4 можно решить, пользуясь предельным признаком сравнения.

Пример 4.1. Исследовать на сходимость ряд

∞

∑ arcsin

(4.1)

(n 2

n=1

Решение. Так как

arcsin

при n → ∞ , то

(n2

+ 3)52

(n 2

+ 3)5 2

lim arcsin

lim

n → ∞

+ 5

n → ∞

+ 3

= lim

= 1.

n → ∞

∞

Кроме того, ряд ∑

сходится, следовательно, ряд (4.1) также сходится.

n=1 n4

Пример 4.2. Исследовать на сходимость ряд

∞

(4.2)

∑

n = 1 2

−1

Решение. Так как ряд

∞

5 n

расходится и

∑

n = 1

5 n

lim

= 1,

то ряд (4.2) также

n → ∞

−1

n → ∞

−1

n → ∞ 1−

расходится.

2.5. Указания к задаче 5

∞

Если члены ряда a1 + a2 + ... + an + ... = ∑ an (5.1)

n=1

таковы, что существует конечный предел

lim

an +1

= l , то при 0 ≤ l < 1 ряд

l > 1 ─

n → ∞

при l = 1 требуется

(5.1) сходится абсолютно, при

расходится, а

дополнительное исследование (признак Даламбера).

Пример 5.1. Исследовать на сходимость ряд

∞ 1

4 7...(3n − 2)

∑

(5.2)

2n+1 n!

n=1

Решение. Имеем

an =

1 4 7...(3n − 2)

2n+1 n!

an+1 =

1 4 7...(3n − 2)(3(n +1)− 2)

1 4 7...(3n − 2)(3n +1)

2(n+1)+1 (n +1)!

2n+2 (n +1)!

lim

n +1

lim

1 4 7...(3n − 2)(3n +1) 2n +1n!

lim

3n +1

> 1 ,

2n + 2 (n +1)!1 4 7...(3n − 2)

n → ∞

n → ∞ 2(n +1)

следовательно, ряд (5.2) расходится.

2.6. Указания к задаче 6

Если существует конечный предел

n a

∞

lim

= l , то при 0 ≤ l <1 ряд ∑ an

n → ∞

n=1

при l >1 ─

l =1 ─

сходится

абсолютно,

расходится,

при

требуется

дополнительное исследование (признак Коши).

Пример 6.1. Исследовать на сходимость ряд

∞

∑n4 arctg 2n

(6.1)

n=1

Решение. Имеем

lim n n

4arctg

2n π =

n arctg

(6.2)

lim

= 0,

n → ∞

так

как

lim x

1x = 1

Действительно,

логарифмируя

функцию

y = x 1x ,

x → ∞

получаем ln y =

ln x

, отсюда по правилу Лопиталя

lim

ln y =

lim

ln x

lim

= 0 ,

x → +∞

x → +∞ x

x → +∞

следовательно,

lim

y = e0 = 1, т.е.

lim

1x = 1.

x → +∞

Из равенства (6.2) следует, что ряд (6.1) сходится.

2.7. Указания к задаче 7
Если an = f (n), где функция f (x)		непрерывная в промежутке [1, ∞), а при
x ≥ d ≥1 неотрицательная и невозрастающая,			∞		∞
x ≥ d ≥1 неотрицательная и невозрастающая,			то ряд ∑ a n	и интеграл	∫ f (x)dx
			n=1		d
сходятся или расходятся одновременно (интегральный признак Коши).
Пример 7.1. Исследовать на сходимость ряд
∞		3n
∑n=2	(n2	− 2)ln 2n			(7.1)

Решение. Рассмотрим вспомогательный ряд

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.04.2019210.96 Кб5BILYeT_1.docx
#
18.09.2019744.45 Кб7Biznes-_plan_Kopirka.doc
#
08.05.2019171.01 Кб35BZhD_modul_2.doc
#
20.04.2015233.47 Кб68c-rigra.doc
#
23.03.20161.36 Mб462ChM_Laboratorny_praktikum_s_ispravleniami.pdf
#
23.03.2016357.17 Кб5Chumakin.pdf
#
23.03.2016328.16 Кб17cMS_lec.pdf
#
09.11.2018108.47 Кб8compilers.docx
#
23.03.201629.39 Mб3Dinox 2013 рус.pdf
#
20.04.201588.58 Кб9document.doc
#
24.05.20152.52 Mб1487Dzhaggernaut_metod_2_0.pdf