Тема 2.6. Кручение(4.6. – авто)

(эзс – 2 час, арх – 1 час, авто – 2)

Кручение прямого бруса круглого сечения.

1. Кручение – вид нагружения, при котором в поперечных сечениях возникает толькокрутящий момент.

2. Прочие внутренние силовые факторы (нормальная и поперечная силы, изгибающие моменты) равны нулю.

3. Пример: круглый брус, жёстко заделанный в стену. На свободном торце приложен скручивающий момент М.

Деформации

От скручивающего момента брус деформируется:

1. Смежные сечения поворачиваются относительно друг друга

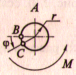
2. Образующая ОВ искривляется и занимает положение АС

Допущения при рассмотрении кручения

1. Ось бруса не деформируется

2. Плоские до деформации поперечные сечения остаются плоскими и после деформации

3. Продольные волокна не изменяют своей длины (угол γ настолько мал, что изменением длины можно пренебречь)

Правило знаков для крутящих моментов

1. Если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит внутренний крутящий момент М_кр против часовой стрелки, то момент считается положительным.

2. По часовой стрелке - отрицательным.

Напряжения в поперечном сечении бруса при кручении.

А) При кручении в поперечном сечении бруса возникают касательные напряжения (чистый сдвиг)

Б) касательные напряжения τ при кручении распределяются в сечении по линейной зависимости:в центре равны нулю, на максимальном радиусе – максимальное значениеτ_max (по которому ведётся расчёт)

В) Значение τ_maxзависит от внутреннего крутящего момента и геометрической характеристики поперечного сечения

τ_max = М_кр\W_р

W_р – полярный момент сопротивления

W_р = 0,2D³– для сплошного сечения

W_р = 0,2D³(1 –d⁴\D⁴)

d– внутренний диаметр (диаметр отверстия)

D– внешний диаметр бруса (авто – вала)

Понятие угла закручивания

А) существуют понятия угла закручивания φ и относительного угла закручивания θ

Б) зависимость между φ и θ

θ = φ\l

φ = М_крl\GW_pr

W_pr = J_p – полярный момент инерции сечения

J_p= 0,1D⁴– для сплошного круглого бруса

J_p= 0,1D⁴(1 –d⁴\D⁴) – для полого круглого бруса

G J_p – жёсткость поперечного бруса при кручении

Построение эпюр крутящих моментов, касательных напряжений и углов закручивания

1. При кручении, как и при растяжении, строят:

А) эпюры внутренних силовых факторов – крутящих моментов (при растяжении – нормальных сил);

Б) эпюры касательных напряжений τ(при растяжении – нормальныхσ)

В) эпюры углов закручивания φ(при растяжении – перемещений)

2. Рисунок стр.78

- разделим брус на 3 части – до силы М₂, от силы М₂до силы М₁, после силы М₁

3. Условное обозначение:

А) кружок с точкой – сила, направленная на наблюдателя;

Б) кружок с крестиком - сила, направленная от наблюдателя.

Построение эпюры Мкр

1. Участок IIIне загружен – момент на эпюре равен нулю.

2. М₁– сила направлена против часовой стрелки: знак +

На эпюре от силы М₂до силы М₁–на участкеIIзначение 2М

Контроль: на эпюре скачок 2М

3. В точке воздействия М₂: +М₁– М₂= 2М-М = М

– на участке Iзначение М

Контроль: на эпюре скачок М

Построение эпюры τ _max

τ_max = М_кр\W_р

1. Участок I

М_{кр =} +М (с эпюры М_кр→W_p= 0,2•(2d)³ = 1,6d³τ _max= М/1,6d³

2. Участок II

М_{кр =} +МW_p= 0,2d³ →W_p= 0,2•(d)³ = 0,2d³ τ _max= М/0,2d³•5\5 = 5М\d³

3. Участок III

М_кр = +2МW_p= 0,2d³ τ _max= 2М/0,2d³•5\5 = 10М\d³

4. Участок IV

М_кр = 0W_p= 0,2d³ τ _max= 0\0,2d³ = 0

W_p– полярный момент сопротивления (геометрический фактор, на который воздействует изгибающий момент)

Для сплошного сечения W_p= 0,2D³

Так как все внутренние крутящие моменты имели положительный знак, то и касательные напряжения τ _max будут положительны.

Построение эпюры φ(углов закручивания)

1. Участок I

φ= М_крIl:GJ_pI= М• l\G• 0,1(2d)⁴ = Мl\G• 0,1•2•2•2•2•d⁴=М • l \ G •1,6•d⁴

2. Участок II

φ = М_крII l:GJ_pII

М • l	+	М • l
G •1,6•d4		G• 0,1d4

Под общий знаменатель принимаем G•d⁴

(1 : 1,6 = 0,6 1 : 0,1 = 10)

0,6 М • l+ 10 М• l	=	10,6 М • l
G•d4		G •d4

3. Участок III

φ = М_крIII • l:GJ_pIII

10,6 М • l	+	2М • l	=	10,6 М • l+ 20М• l	=	30,6М •l
G •d4		G• 0,1d4		G•d4		G•d4

3. Участок IV

30,6М •l\G•d⁴+ 0•l\G•d⁴= 30,6М•l\G•d⁴(постоянная величина на этом участке)

Условия прочности и жесткости при кручении

1. Условие прочности бруса при кручении

τ _кр ^max R_кр или

М_кр\W_pR_кр

где R_кр – расчётное сопротивление материала кручению.

1. Условие жёсткости бруса при кручении

θ [θ]

θ – относительный угол закручивания

[θ] – допускаемый относительный угол закручивания, принимают по СНиП в заваисимости о материала бруса.

θ = М_кр\GJ_p

G – модуль поперечной деформации

Три типа задач при расчете на прочность и жесткость при кручении

1. Проектировочный расчёт – определение диаметра бруса при заданной нагрузки

2. Проверочный расчёт – определение в брусе максимального касательного напряжения от заданной нагрузки и сравнение его с допустимым

3. Расчёт допускаемой нагрузки – расчёт допускаемой нагрузки для бруса (вала) заданного сечения (размеры и материал).

Самостоятельная работа (эзс – нет, арх – 1 нет, авто – 2)

1. Выполнение расчётно­-графической работы на построение эпюр крутящих моментов, углов закручивания и расчёт на прочность и жёсткость при кручении - авто