element_geometrija_stereometrija_tom_2

а ребра триэдра принадлежат образующим. Он называется конусом,

описанным около данного триэдра.

4.4. Высотные плоскости и ортоось триэдра. Три плоскости, каждая из которых проходит через ребро триэдра перпендикулярно плоскости противоположной грани, называются высотными плоскостями этого триэдра. Они определены однозначно, если ни одно ребро триэдра не перпендикулярно противоположной грани. Будем предполагать это ограничение.

Теорема 3. Три высотные плоскости триэдра имеют общую прямую. Она называется ортоосью триэдра.

Д о к а з а т е л ь с т в о. Обозначим буквой a то ребро триэдра Oabc, которое не перпендикулярно остальным. Пусть плоскость p перпендикулярна ребру a и пересекает его в точке A, а прямые, содержащие ребра b и c, — в точках B и C (рис. 30). Пусть плоскость OAM перпендикулярна

N

Рис. 30

BC, M (BC). Плоскость OBC содержит перпендикуляр BC к плоскости OAM, поэтому эти плоскости перпендикулярны. Построим плоскость OCN, перпендикулярную плоскости OAB. Тогда плоскости OAM

иOCN — высотные плоскости данного триэдра. Так как плоскости p

иOCN перпендикулярны плоскости OAB, то прямая NC их пересечения перпендикулярна плоскости OAB. Прямые AM и CN — высоты треугольника ABC. Следовательно, если (AM) ∩ (CN) = H, то BH — третья высота этого треугольника. Поскольку OA BH и AC BH, то плоскость OAC перпендикулярна BH, и поэтому плоскости OAC и OBH перпендикулярны (вторая из них содержит перпендикуляр BH к первой). Итак, плоскость OBH — третья высотная плоскость триэд-

ра, а прямая OH — его ортоось.

41

Следствие 1. Если плоскость p перпендикулярна ребру триэдра, то ортоцентр H треугольника ABC ее пересечения с триэдром принадлежит ортооси триэдра.

Согласно определению ортооси каждое ребро служит ортоосью триэдра, ребрами которого является два других ребра данного триэдра и его ортоось: если h — ортоось триэдра Oabc, то a — ортоось триэдра Ohbc и т. д. Поэтому предыдущее следствие можно переформулировать так.

Следствие 2. Если плоскость перпендикулярна ортооси триэдра, то ортоцентр треугольника ее пересечения с триэдром принадлежит ортооси.

Теорема 4. Если ортоось триэдра лежит внутри него, то высотные плоскости триэдра пересекают соответственные им грани по лучам a1, b1, c1, образующим такой триэдр, для которого эти высотные плоскости являются биссекторными плоскостями двугранных углов (рис. 31).

c1

B1

b

A H

A1

C1

B

Рис. 31

Д о к а з а т е л ь с т в о. Пусть плоскость ABC перпендикулярна ортооси h триэдра Oabc. Согласно следствию 2 точка H = h ∩ (ABC) есть ортоцентр треугольника ABC. Из планиметрии известно, что лучи AH, BH, CH делят пополам углы треугольника ABC с вершинами в основаниях высот треугольника ABC. Так как смежные двугранные углы с общим ребром A1H прямые, то согласно (2.7) из равенства углов B1A1H и C1A1H следует равенство углов OA1B1 и OA1C1. В триэдрах A1(OB1H) и A1(OC1H) соответственные плоские углы равны. Поскольку все они острые, то по теореме синусов (2.9) следует равенство соответственных двугранных углов. Итак, двугранные углы этих триэдров с общим ребром OA1 равны. Аналогично и другие высотные плоскости триэдра Oabc делят пополам двугранные углы триэдра Oa1b1c1.

42

§5. Плоскости, перпендикулярные осям описанного и вписанного конусов триэдра

5.1.Плоскость перпендикулярная оси конуса, описанного около триэдра. Рассматривается круговой конус, содержащий ребра триэдра своими образующими. Его ось l образует равные углы с ребрами. Рассмотрим плоскость d, содержащую вершину триэдра и перпендикулярную оси l конуса. Ребра триэдра равнонаклонены к плоскости d.

Теорема 5. Плоскость d, перпендикулярная оси описанного около триэдра конуса, проходящая через его вершину, содержит биссектрисы углов, смежных с плоскими углами этого триэдра.

Предварительно докажем следующую лемму.

Лемма. Для того чтобы плоскость, проходящая через вершину угла, была равнонаклонена к его сторонам, необходимо и достаточно, чтобы она содержала биссектрису этого угла или биссектрису смежного с ним угла.

Д о к а з а т е л ь с т в о. Д о с т а т о ч н о с т ь. Пусть плоскость a проходит через биссектрису m угла AOB (рис. 32). При симметрии с осью m плоскость a отображается на себя, луч

43

Переходим к доказательству сформулированной выше теоремы. Плоскость d равнонаклонена к ребрам триэдра и она не имеет с триэдром общих внутренних точек. На основании леммы она содержит биссектрисы углов, смежных с плоскими углами триэдра.

Кроме плоскости d, существуют еще три плоскости, каждая из которых равнонаклонена к ребрам данного триэдра. Эти плоскости перпендикулярны к осям конусов, описанных соответственно около триэдров, смежных с данным (см. п. 1.1). Каждая из них содержит биссектрисы двух плоских углов данного триэдра и биссектрису угла, смежного с его третьим плоским углом.

5.2. Плоскость, перпендикулярная оси вписанного в триэдр конуса.

Ось вписанного в триэдр конуса образует равные углы с его гранями и образует равные углы с ребрами полярного ему триэдра, поэтому служит осью описанного около него конуса. Обратно, ось описанного около триэдра конуса образует равные углы с гранями триэдра, полярного данному, т. е. является для него осью вписанного конуса.

Плоскость, перпендикулярная оси вписанного в триэдр конуса, равнонаклонена к плоскостям его граней.

Теорема 6. Плоскость w, перпендикулярная оси l вписанного в триэдр конуса и проходящая через его вершину, содержит три прямые u1, u2, u3, каждая из которых лежит в биссекторной плоскости двугранного угла, смежного с одним двугранным углом данного триэдра, проходит через его вершину перпендикулярно соответствующему ребру.

Д о к а з а т е л ь с т в о. Пусть дан триэдр Oabc. Через его вершину проведем плоскость a, перпендикулярную ребру a. Прямая u1 = a ∩ w удовлетворяет заданным условиям. Действительно, она принадлежит биссекторной плоскости двугранного угла, смежного с двугранным углом при ребре a, так как эта плоскость перпендикулярна биссекторной плоскости (l, a), а биссекторные плоскости смежных двугранных углов перпендикулярны. Так как a a, то u1 a. Аналогично строятся две другие прямые u2 и u3 плоскости w, удовлетворяющие указанным в теореме условиям.

Кроме плоскости w существуют еще три плоскости, каждая из которых содержит вершину данного триэдра и равнонаклонена к плоскостям его граней. Они перпендикулярны соответственно осям конусов, вписанных в триэдры, смежные с данным триэдром.

З а д а ч а 1. Дан триэдр, ни одно ребро которого не перпендикулярно противоположной грани. Через вершину триэдра в плоскости каждой его грани проведена прямая, перпендикулярная противополож-

44

ному ребру. Докажите, что полученные таким образом три прямые лежат в одной плоскости c, перпендикулярной ортооси триэдра.

Ре ш е н и е. Пусть прямая p лежит в плоскости Obc и перпендикулярна ребру a триэдра Oabc, O p. Прямая a1 пересечения плоскости Obc с высотной плоскостью, содержащей ребро a, есть проекция прямой a на плоскость Obc. По теореме о трех перпендикулярах p a1. Следовательно, прямая p перпендикулярна высотной плоскости и ортооси триэдра. По аналогичной причине две другие прямые, удовлетворяющие условиям задачи, перпендикулярны ортооси. Поэтому все три эти прямые лежат в одной плоскости c.

З а д а ч а 2. Докажите, что прямые, содержащие биссектрисы углов, смежных с плоскими углами триэдра, лежат в одной плоскости, равнонаклоненной к трем ребрам триэдра.

Ре ш е н и е. На ребрах триэдра отложим равные отрезки OA, OB, OC. Векторы OA − OB, OB − OC, OC − OA соответственно коллинеарны указанным прямым. Сумма этих векторов равна нуль-вектору, поэтому они компланарны, а эти прямые лежат в одной плоскости, так как имеют общую точку O. По лемме пункта 5.1 эта плоскость равнонаклонена к ребрам триэдра.

§6. Начальные сведения о сферической геометрии

6.1.Основные понятия. Сферическая геометрия возникла в связи

спотребностями астрономии. В сферической геометрии роль прямых играют большие окружности сферы, т. е. окружности, являющиеся сечениями сферы плоскостями, проходящими через ее центр. Через две точки A и B сферы, не принадлежащие одному диаметру, можно провести единственную большую окружность, которая точками A и B разбивается на две дуги — два сферических отрезка. Длину меньшей из этих дуг принимают за расстояние между данными точками, которое удобно измерять величиной соответствующего центрального угла. Если углы измерять в радианах, то на сфере радиуса 1 такое измерение сферического отрезка равно обычной длине дуги.

Любые две большие окружности пересекаются в двух диаметрально противоположных точках сферы. Поэтому в сферической геометрии нет параллельных больших окружностей. Геометрия на сфере является неевклидовой — первой из неевклидовых геометрий.

Угол между большими окружностями определяется как угол между их плоскостями. А он равен углу между касательными к этим окруж-

45

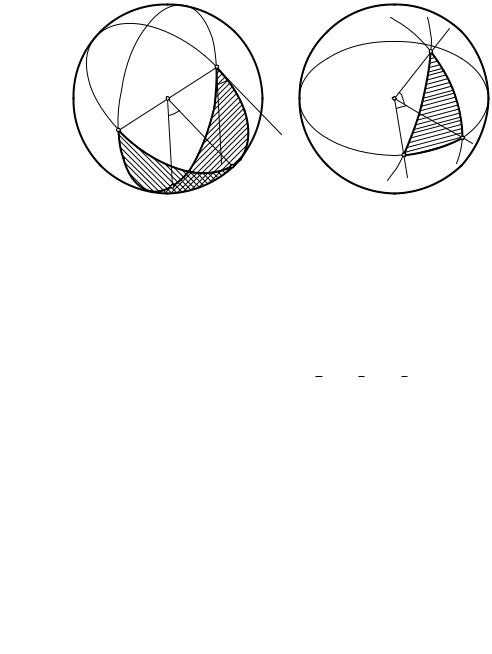
ностям в точке их пересечения (рис. 33). Три большие окружности сферы разбивают ее на восемь областей, называемых сферическими треугольниками.

6.2. Связь геометрии трехгранного угла со сферической геометрией. Все формулы и теоремы, относящиеся к трехгранному углу, можно истолковать в терминах сферической геометрии следующим образом. Построим сферу единичного радиуса с центром в вершине O триэдра. Тогда его ребра определяют некоторый сферический треугольник ABC (рис. 34). Углы A,b B,b Cb сферического треугольника ABC измеряются двугранными углами триэдра, а стороны a, b, c — его плоскими углами a, b, g.

Если радиус сферы равен r, то a = ar , b = rb , g = rc — радианные меры этих углов. Отсюда каждая формула для триэдра имеет определенный смысл в сферической геометрии и обратно. Так, например, равенства (2.5), (2.6), (2.9) выражают смысл теорем косинусов и теоремы синусов для сферического треугольника. Равенства (2.13) означают, что произведение синуса стороны сферического треугольника и синуса соответствующей его высоты постоянно для данного треугольника.

Полярным триэдрам соответствуют на сфере полярные сферические треугольники ABC и A0B0C0, между сторонами и углами которых имеет место полярная зависимость: a + Ab0 = b + Bb0 = c + Cb0 = p

и a0 + Ab= b0 + Bb = c0 + Cb = p.

Биссекторной плоскости двугранного угла триэдра соответствует биссектриса сферического треугольника. Поэтому теорема пункта 4.2 означает, что биссектрисы сферического треугольника пересекаются

46

в одной точке, равноудаленной от его сторон. Биссектрисе плоского угла триэдра соответствует середина стороны сферического треугольника. Согласно теореме пункта 4.1 медианы сферического треугольника пересекаются в одной точке. Теорема п. 4.3 гласит: серединные перпендикуляры к сторонам сферического треугольника пересекаются в одной точке. Теорема об ортооси (п. 4.4) может быть переформулирована так: высоты сферического треугольника пересекаются в одной точке.

Описанный и вписанный конусы триэдра высекают на сфере «малые» окружности — соответственно описанную и вписанную окружности треугольника на сфере.

Нет надобности переводить на язык сферической геометрии все формулы и теоремы этой главы. Читатель при желании может это сделать сам.

Задачи к главе 2

2.1.Докажите, что триэдры равны, если равны их соответственные двугранные углы.

2.2.Луч OM лежит внутри триэдра O(ABC). Докажите, что сумма плоских углов триэдра O(ABC) больше суммы плоских углов триэдра

O(ABM).

2.3.Если все плоские углы триэдра тупые, то и все его двугранные углы также тупые. Докажите это утверждение и обратное ему утверждение.

2.4.В правильной треугольной пирамиде двугранный угол при боковом ребре имеет величину a. Найдите величину двугранного угла при основании.

2.5.В триэдре величина каждого плоского угла равна a. Найдите величину его двугранного угла.

2.6.В правильной треугольной пирамиде двугранный угол при основании равен f. Найдите величину двугранного угла при боковом ребре.

2.7.Плоский угол при вершине правильной треугольной пирамиды равен a. Найдите величину двугранного угла при основании.

2.8.В триэдр с вершиной O вписана сфера с центром S. Докажите, что прямая OS перпендикулярна плоскости, содержащей точки касания.

2.9.В триэдр O(ABC) вписана сфера, касающаяся его граней в точках A1, B1, C1. Выразите величину угла AOB1 через величины плоских углов триэдра.

47

2.10.В правильной четырехугольной пирамиде плоский угол при вершине равен a. Найдите угол между противоположными боковыми гранями.

2.11.В треугольной пирамиде ABCD грани ABC и ABD — прямоугольные равнобедренные треугольники с общей гипотенузой AB. Угол между ними равен a. Найдите величину двугранного угла при ребре BC.

2.12.В триэдре O(ABC) сумма углов AOB и AOC равна 180◦. Вычислите угол между ребром OA и биссектрисой угла BOC.

2.13.Плоские углы триэдра имеют величину a. Найдите угол между его ребром и осью описанного около него конуса.

2.14.В правильный триэдр с плоским углом a вписан конус. Определите угол между ребром триэдра и осью этого конуса.

2.15.Плоские углы триэдра имеют величину a. Точка M внутренней области триэдра удалена от каждой его грани на расстояние a. Вычислите расстояние от точки M до вершины триэдра.

2.16.Докажите, что углы между биссектрисами плоских углов триэдра либо все одновременно острые, либо все тупые, либо все прямые.

2.17.Докажите, что сумма косинусов двугранных углов триэдра меньше 1,5.

2.18.Даны три попарно скрещивающиеся прямые, не параллельные одной плоскости, и на одной из них точка P . Постройте плоскость, содержащую данную точку P и образующую равные углы с этими прямыми.

2.19.Через данную точку проведите плоскость, пересекающую ребра данного триэдра под равными углами.

2.20.Все плоские углы триэдра прямые. Постройте плоскость, пересекающую этот триэдр по треугольнику, который равен заданному остроугольному треугольнику.

2.21.Постройте триэдр по его заданным плоским углам.

2.22.Постройте триэдр по его заданным двугранным углам.

2.23.Дан триэдр O(ABC), у которого плоские углы BOC и COA равны. В плоскостях COA и BOC выбраны соответственно лучи u, v

сначалом O, лежащие по разные стороны от плоскости AOB так, что угол (OA, u) равен углу (OB, v). Докажите, что биссектриса угла(u, v) и ребра OA и OB лежат в одной плоскости.

2.24.Даны три плоскости, содержащие общую прямую, и луч, лежащий в одной из них и имеющий начало на этой прямой. Постройте триэдр, обладающий тем свойством, что каждая из данных плоскостей проходит через одно из его ребер и перпендикулярна противолежащей грани, причем одним из ребер служит данный луч.

48

2.25.Даны три прямые в одной плоскости и плоскость a, проходящая через одну из них. Постройте триэдр, обладающий тем свойствам, что каждая из данных прямых перпендикулярна одному из ребер и лежит в противолежащей грани, причем одна из граней лежит в плоскости a.

2.26.Докажите, что синус Штаудта триэдра может быть выра-

жен так:

Δ(O) = 2psin c sin(c − a) sin(c − b) sin(c − g), где c = 12 (a + b + g).

2.27. Докажите, что плоские углы любого триэдра удовлетворяют

неравенству:

ab + bg + ga < 43 p2.

2.28.В треугольной пирамиде сумма плоских углов при вершине больше 180◦. Докажите, что каждое боковое ребро меньше полупериметра основания.

2.29.Докажите, что если в триэдре O(ABC) двугранный угол при

ребре OC равен 90◦, то sin a = tg b ctg Bb.

2.30.Сечением куба плоскостью, содержащей его вершину, является равнобедренный треугольник с углом a между неравными сторонами. Найдите углы наклона плоскости сечения к плоскостям граней куба.

2.31.Если прямая образует равные углы с тремя непараллельными прямыми плоскости, то она перпендикулярна этой плоскости. Докажите.

2.32.Для того чтобы в четырехгранный угол можно было вписать сферу, необходимо и достаточно, чтобы суммы его противоположных двугранных углов были равны. Докажите.

49