
element_geometrija_stereometrija_tom_2
.pdf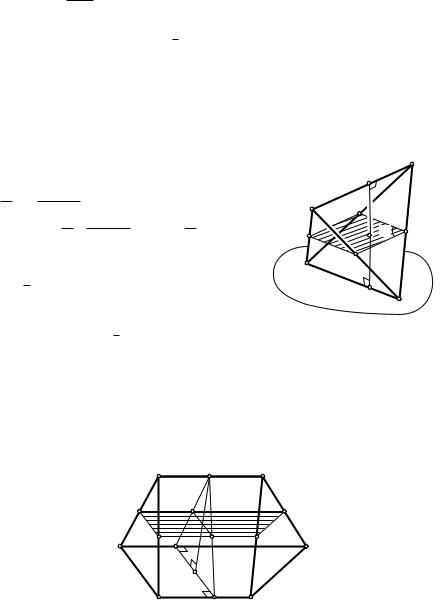
Для усеченного конуса имеем тот же результат. Для него S = pr2,
√ 1 1
S2 = pr22, S1S2 = pr1r2 и, следовательно,
V = 13 ph(r12 + r22 + r1r2).
|
Получим формулу Сервуа (6.14) для объема тетраэдра, пользуясь |
||||||||||
формулой Ньютона–Симпсона. Проведем две параллельные плоскости |
|||||||||||
через скрещивающиеся ребра тетраэдра (рис. 91). Пусть a и a1 — длины |
|||||||||||
этих ребер, f — угол между ними, d — кратчайшее расстояние. Сечени- |
|||||||||||
ем тетраэдра плоскостью, параллельной этим ребрам, является парал- |
|||||||||||
лелограмм. Если x — расстояние секущей |
|
|
|||||||||
плоскости от |
ребра длины a, то сторо- |
|
D |
||||||||
ны этого параллелограмма имеют длины |
|
a |
|||||||||
bx |
и |
a(d − x) |
, поэтому его площадь рав- |
|
|||||||
A |
|
||||||||||
d |
|
|
d |
a(d − x) |
|
sin f = abx(d |
|
|
|
|
d |
на |
S(x) = bx |
· |
− |
x) |
× |
|
|
||||
|
|
d · |
d |
d2 |
|
|
f |
||||
× sin f. Как видим, S(x) — квадратичная |
|
|
|||||||||
функция, для которой S(0) = 0, S(d) = 0, |
B |
|
|||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
4S 2 = ab sin f. Согласно формуле |
(7.2) |
a1 |
|
C |
|||
объем V тетраэдра равен |
|
||
|
|
||
V = 1 ab sin f. |
|
Рис. 91 |
|
2 d |
|
|
1.3. Объем клина. Формула (6.20) объема клина была получена в п. 3.7 гл. 6. Рассмотрим другое ее д о к а з а т е л ь с т в о, опуская проверку условия применимости формулы Ньютона–Симпсона. Поставим клин ABCA1B1C1 на боковую грань AA1B1B с параллельными ребрами a и b (рис. 92). Пусть d — длина высоты трапеции AA1B1B.
C |
c |
M |
C1 |
b |
|
|
|
B |
Q |
h |
B1 |
A |
a |
P |
A1 |
|
|||
|
|
Рис. 92 |
|
121
Тогда ее площадь S1 = 12 (a + b)d. Площадь S среднего сечения клина,
которое является трапецией с основаниями 12 (a + c) и 12 (b + c) и вы-
сотой 12 d, равна 12 12 (a + c) + 12 (b + c) 12 d = 18 (a + b + 2c)d. Если h — расстояние от ребра CC1 до плоскости грани AA1B1B, то по формуле
Ньютона–Симпсона объем V клина равен
V = 0 + 12 (a + b)d + 4 · 18 (a + b + 2c)d = h6 · d2 · 2(a + b + c).
Заметим, что 12 hd есть площадь S перпендикулярного сечения MP Q клина. В результате имеем:
1
V = 3 S (a + b + c).
Опущенная часть этого доказательства — выражение площади произвольного сечения, параллельного плоскости грани AA1B1B,
S(x) = S1 − dcx2 + dcx h2 h
—может быть самостоятельно восполнена читателем.
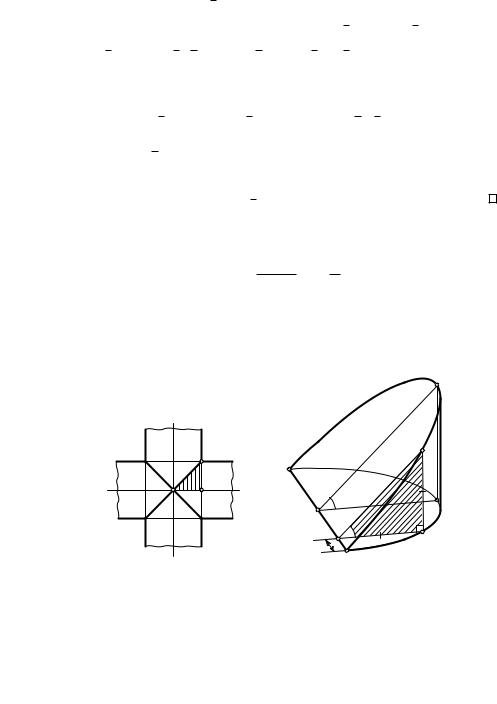
За д а ч а. Оси двух круговых цилиндров равных радиусов R пересекаются под прямым углом. Требуется найти объем тела, являющегося пересечением этих цилиндров (рис. 93).
Q
R
|
B |
|
|
Q |
|
|
P |
|
O |
R |
|
P |
||
|
|
O |
|
|
A |
C |
|
x |
|
|
|
|
Рис. 93 |
|
Рис. 94 |
Р е ш е н и е. Пересечением данных цилиндров является тело, состо- ящее из четырех равных частей, каждую из которых можно разбить пополам. Одна из полученных восьми долек представлена на рис. 94.
122

Ее параллельными сечениями плоскостями, параллельными плоскости симметрии OP Q, служат равнобедренные прямоугольные треугольники. Если x — расстояние секущей плоскости от конца диаметра ци-
линдра, то площадь S(x) сечения ABC равна 12 AC2 = 12 x(2R − x), следовательно, является квадратичной функцией. По формуле Ньютона– Симпсона при h = 2R, 0 6 x 6 2R, S = 12 R2 искомый объем пересечения цилиндров будет равен:
V= 8 · 26R(0 + 0 + 4 · 12 R2) = 163 R3.
§2. Объем шара и его частей
2.1.Объем шара и шарового сегмента. Вычислим объем V шара радиуса R по формуле Ньютона–Симпсона, что чрезвычайно просто: площади его «крайних» сечений равны нулю, а площадь среднего сечения равна pR2. Тогда
V = 26R (0 + 0 + 4pR2) = 43 pR3.
Однако прежде нужно было убедиться в том, что площадь S(x) его произвольного сечения — квадратичная функция. А это так:
S(x) = pr2 = px(2R − x) = −px2 + 2pRx,
где r — радиус сечения, x — расстояние от плоскости сечения до параллельной ей касательной плоскости к шару.
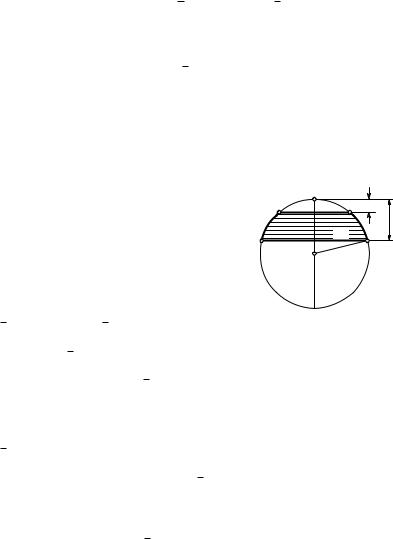
Шаровым сегментом называется часть шара, отсеченная от него некоторой секущей плоскостью (рис. 95). Круг, являющийся сечени-
N 
r1
h
r
P |
R |
O |
|
Рис. 95 |
|
ем шара этой плоскостью, называется основанием шарового сегмента. Плоскость, пересекающая шар, делит его на два шаровых сегмента с общим основанием. Если провести касательную плоскость к шаровому
123
сегменту, параллельную его основанию, то расстояние h между этой плоскостью и плоскостью основания называется высотой сегмента.
Радиус r основания, радиус R шара и высота h сегмента связаны зависимостью:
r2 = h(2R − h). |
(7.3) |
По этой же формуле для радиуса r1 среднего сечения шарового сегмента имеем: r12 = h2 2R − h2 . Тогда по формуле Ньютона–Симпсона объем
V шарового сегмента с высотой h будет равен:
|
h |
|
|
h |
|
|
|
|
|
p |
2 |
|
|
|
|
− |
h |
|
||||||
V = |
|
(0 + pr2 + 4pr12) = |
|
ph(2R − h) + 2ph 2R |
|
|
|
= |
|
|||||||||||||||
6 |
6 |
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
2 h |
R − |
h |
+ 2R − |
h |
= |
1 |
ph2(3R − h). |
||||||||
|
|
|
|
|
|
|
6 |
2 |
2 |
3 |
||||||||||||||
Итак, |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
V = |
ph2(3R − h). |
|
|
|
|
(7.4) |
|||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||
Из (7.3) R = |
1 |
(r2 |
+ h2). Поэтому из (7.4) получаем еще другую фор- |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
|
2h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мулу для объема шарового сегмента: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
V = |
1 |
h(3r2 |
+ h2). |
|
|
|
|
(7.5) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
6 p |
|
|
|
|
|
|
|
|
|
|
|
|
||||
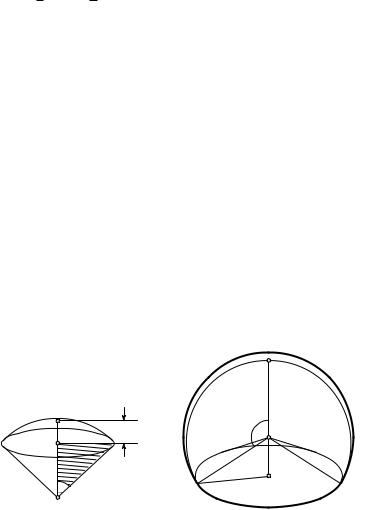
2.2. Объем шарового сектора. Шаровым сектором называется тело вращения кругового сектора около его граничного радиуса. Пусть центральный угол кругового сектора равен a. Возможны три случая: a < 90◦, 90◦ < a < 180◦ и a = 90◦. Для первых двух случаев соответствующие шаровые секторы изображены на рис. 96 и рис. 97. При a < 90◦ шаровой сектор состоит из шарового сегмента и конуса. Во втором слу-
|
|
N |
|
N |
h |
a O |
|
r |
|||
|
|
||
|
R |
r |
|
a |
|
||
|
|
||
O |
|
|
|
Рис. 96 |
|
Рис. 97 |
124
чае шаровой сектор представляет собой разность шарового сегмента |
||
и конуса. Случай a = 90◦ исключается из рассмотрения, поскольку то- |
||
гда шаровой сектор есть полушар. Высоту h шарового сегмента, соот- |
||
ветствующего данному шаровому сектору, называют также и высотой |
||
этого сектора. |
|
|
В случае a < 90◦ объем V шарового сектора находится как сумма |
||
объемов сегмента и конуса: V = 31 ph2(3R − h) + 31 pr2(R − h), где R — |
||
радиус шара, r — радиус основания сегмента и конуса. После подста- |
||
новки (7.3) и упрощения полученного выражения имеем окончательно: |
||
V = 2 R2h. |
|
(7.6) |
3 p |
|
|
При a > 90◦ высота конуса будет равна h −R, но тогда вместо суммы |
||
объемов имеем их разность. В результате получается тот же резуль- |
||
тат (7.6). |
|
|
2.3. Объем шарового слоя и шарового кольца. Шаровым слоем назы- |
||
вается часть шара, заключенная между двумя его секущими параллель- |
||
ными плоскостями. Расстояние между этими |
|
|
плоскостями называется высотой шарового |
|
|
слоя. |
r1 |
h1 |
Шаровой слой представляет собой раз- |
|
h2 |
ность двух шаровых сегментов. Если h1 и |
|
r2 |
|
|
|
h2 — высоты этих сегментов, r1 и r2 — ра- |
O |
R |
диусы их оснований (рис. 98), то объем V |
|
|
шарового слоя равен: |
|
|
V = 31 ph22(3R − h2) − 31 ph12(3R − h1) = |
Рис. 98 |
|
= 31 p(3R(h22 − h12) − (h23 − h13)) = |
|
|
= 31 p(h2 − h1)(3R(h2 + h1) − (h12 + h22 + h1h2)). |
||
Согласно (7.3) 2Rhi = ri2 + hi2, (i = 1, 2). Поэтому |
|
|
V = 61 p(h2 − h1)(3(r22 + h22 + r12 + h12) − 2(h12 + h22 + h1h2)) = |
|
|
= 61 p(h2 − h1)(3r12 + 3r22 + (h2 − h1)2). |
||
Так как h2 − h1 = h — высота шарового слоя, то получаем оконча- |
||
тельно: |
|
|
V = 1 h(3r12 + 3r22 + h2). |
|
(7.7) |
6 p |
|
|
125
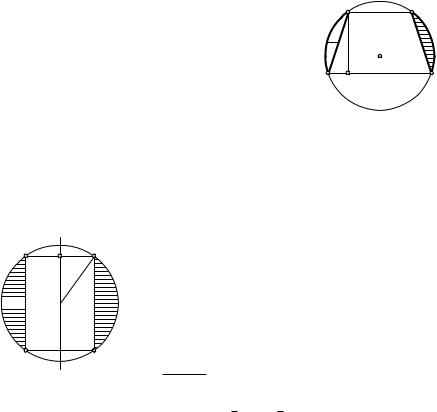
Шаровым кольцом называется тело вращения |
|
r1 |
|||||||||
кругового сегмента около диаметра этого круга, ес- |
|
|
|
||||||||
|
|
|
|||||||||
|
|
|
|||||||||
|
|
|
|||||||||
ли этот диаметр не имеет общих внутренних точек |
|
|
|
||||||||
|
|
|
|||||||||
|
|
|
|||||||||
l |
h |
|
|||||||||
с хордой кругового сегмента (рис. 99). |
|
||||||||||
|
O |
|
|||||||||
|
|
||||||||||
|
|||||||||||
|
|||||||||||
Очевидно объем шарового кольца равен разно- |
|
|
|
||||||||
|
|
|
|||||||||
|
|
|
|||||||||
сти объемов шарового слоя и усеченного конуса: |
|
r2 |
|||||||||
|
|
|
|||||||||
V = |
1 |
ph(3r12 + 3r22 + h2) − |
1 |
ph(r12 + r22 + r1r2) = |
|
|
|||||
6 |
3 |
|
Рис. 99 |
||||||||
= |
1 |
ph(r12 + r22 − 2r1r2 + h2) = |
1 |
ph((r2 − r1)2 + h2). |
|
|
|
||||
6 |
6 |
|
|
|
|||||||
Из соответствующего прямоугольного треугольника (r2 − r1)2 + h2 = l2, где l - длина хорды вращающегося кругового сегмента. Объем шарового кольца, следовательно, выражается простой формулой:
r
R
 l O
l O 
Рис. 100
V = |
1 |
|
l2h. |
(7.8) |
|
6 p |
|||||
|
|
|
|||
Примечательно, что этот объем не зависит от радиуса шара.
З а д а ч а. В шаре радиуса R просверлено вдоль его диаметра цилиндрическое отверстие радиуса r. Найдите объем оставшейся части шара.
Р е ш |
е н и е. |
Оставшаяся |
часть шара есть |
шаровое |
кольцо |
(рис. 100) у |
которого l = h = |
√
= 2 R2 − r2. Поэтому ее объем равен
V= 16 ph3 = 43 p(R2 − r2)3/2.
§3. Принцип Кавальери
3.1.Сущность принципа Кавальери. Итальянский математик Бонавентура Кавальери (1598–1647), ученик Галилея, сформулировал свой принцип для нахождения объемов тел в своей книге, вышедшей в 1635 году. Содержание этого принципа таково.
Если при пересечении двух тел F и F1 плоскостями, параллельными некоторой постоянной плоскости a, в сечениях этих тел получаются фигуры, площади которых находятся в постоянном отношении
l: S = lS1, то объемы этих тел находятся в том же отношении:
V (F ) = lV (F1).
Кавальери высказал этот факт без доказательства как постулат — «принцип». Потом стало ясно, что он является простым следствием
126
формулы (7.1). Но интегральное исчисление появилось позже примерно лет на 25 в работах И. Ньютона и Г. Лейбница благодаря, в частности, и исследованиям Б. Кавальери.
На основании принципа Кавальери пирамиды с равными высотами и равновеликими основаниями равновелики. Отсюда путем разбиения треугольной призмы диагоналями боковых граней на три равновеликие треугольные пирамиды из формулы объема призмы получается основ-
ная формула объема тетраэдра V = 13 Sh.
Рассмотрим другие примеры применения принципа Кавальери.
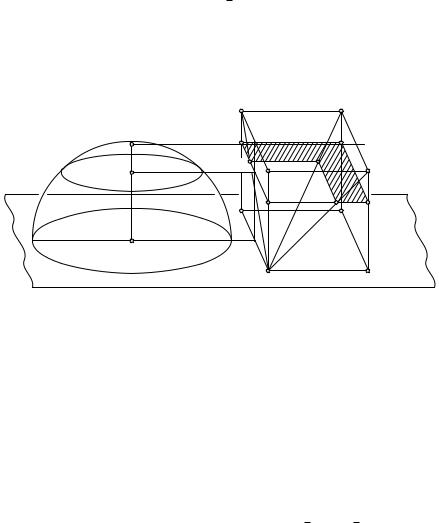
3.2. Объем шара и шарового сегмента. Рассмотрим полушар с центром O радиуса R. Поместим на плоскость a его граничного круга куб с ребром длины R (рис. 101). Отсечем от куба ABCDA1B1C1D1
|
B1 |
|
C1 |
Q |
M |
|
|
|
|
|
|
|
M1 |
|
D1 |
P |
A1 |
|
|
|
|
||
x |
N |
x |
|
B |
|
|
|
|
|
|
C |
|
R |
|
|
O |
|
|
a |
|
A |
R |
D |
|
|
||
|
Рис. 101 |
|
|
четырехугольную пирамиду AA1B1C1D1. Сравним объем полученного многогранника F1 с объемом полушара. Пересечем этот многогранник и полушар некоторой плоскостью b, параллельной a и отстоящей от нее на расстоянии OP = x. В сечении полушара получим круг, площадь которого равна p(R2 − x2). Сечением многогранника F1 является шестиугольник, площадь которого равна разности R2 − x2 площади грани куба и квадрата со стороной x, так как AN = NM1 = x. Следовательно, условия принципа Кавальери выполнены: отношение площадей сечений данных тел постоянно (равно p). Тогда по этому принципу объем полушара равен
pV (F1) = p(Vкуба − VAA1B1C1D1 ) = p R3 − 13 R3 = 23 pR3.
127

Пользуясь выполненными построениями, найдем объем шарового сегмента с высотой h = P Q, отсеченного от полушара секущей плоскостью b. Этому шаровому сегменту соответствует многогранник, полученный путем изъятия из прямоугольного параллелепипеда NC1 (верхней части куба AC1) усеченной пирамиды, одним основанием которой служит квадрат A1B1C1D1 (с ребром R), а другим — квадрат с ребром x. К этим телам также применим принцип Кавальери (с аналогичной секущей плоскостью):
Vшар.сегм. = p R2h − |
1 |
R3 − |
1 |
(R − h)3 = ph2 R − |
h |
. |
3 |
3 |
3 |
Объем усеченной пирамиды подсчитан как разность объемов двух полных пирамид с общей вершиной A.
Полученный результат совпадает с (7.4).
3.3. Объем тора. Тором называется тело, полученное вращением круга около прямой, лежащей в плоскости этого круга и не пересекающей его. Форму тора имеет, например, обыкновенная баранка или же накачанная автомобильная шина.
Для получения формулы объема тора положим его на некоторую плоскость a. Пусть R — радиус вращающегося круга, a — расстояние от центра O1 этого круга до оси вращения. Положим на плоскость a также прямой круговой цилиндр радиуса R с длиной a образующей так, чтобы он касался плоскости a по образующей (рис. 102). Пересечем эти два тела плоскостью g, параллельной плоскости a и удаленной от центров оснований цилиндра на расстояние x. Эта плоскость пересекает тор по круговому кольцу, а цилиндр — по прямоугольнику (на рис. 102 они заштрихованы). Нетрудно подсчитать, что площадь кольца равна
p a + √R2 − x2 2 − p a − √R2 − x2 2 = 4pa√R2 − x2,
√
а площадь прямоугольника — 2a R2 − x2. Их отношение l = 2p не зависит от x. Согласно принципу Кавальери объем тора равен объему цилиндра, умноженному на 2p:
Vтора = 2p · pR2a = 2p2aR2. |
(7.9) |
Так как формулу (7.9) объема тора можно записать в виде pR2 · 2pa, то результат можно сформулировать так.
Объем тора равен произведению площади образующего его круга и длины окружности, радиус которой равен расстоянию от центра этого круга до оси вращения.
128
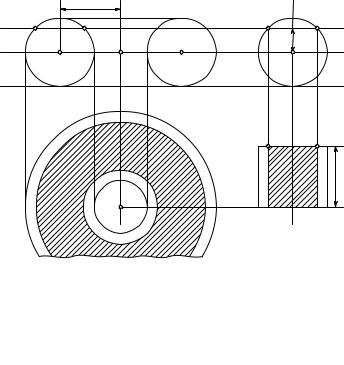
g |
a |
|
|
a |
O1 |
O |
R |
x |
|
|
|
a |
Рис. 102
§4. Объем тела вращения
4.1.Лемма о площади поверхности, образованной вращением отрезка. Площадь S поверхности вращения отрезка, который не имеет общих внутренних точек с осью вращения, лежащей в одной плоскости с отрезком, равна произведению длины l этого отрезка и длины окружности, радиус которой равен расстоянию r от середины отрезка до оси вращения:
S = l · 2pr |
(7.10) |
(теорема Г ю л ь д е н а для отрезка).
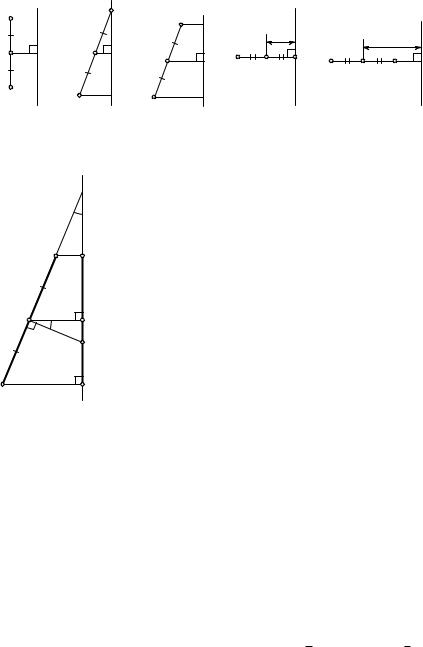
Д о к а з а т е л ь с т в о. Возможные случаи взаимного расположения отрезка AB и оси x вращения представлены на рис. 103. В случае а), когда AB k x, поверхность вращения — боковая поверхность цилиндра. Тогда S = 2prl. При условии б ) получается боковая поверхность конуса с образующей l и радиусом 2r основания. Поэтому S = 2plr. В случае в) площадь боковой поверхности усеченного конуса равна S = pl(r1 + r2) = = 2plr. Когда AB x, получаем либо круг радиуса l = 2r, либо круговое кольцо с площадью S = p(OA2 − OB2) = p(OA + OB)(OA − OB) = = p · 2r · l. 
129
A |
|
A |
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
r |
|
l |
r |
l |
|
|
|
|
|
|
l |
r |
|
|
|
|
|||
|
|
r |
|
B |
|
|
||
|
|
|
A |
l |
|
|
||
|
|
|
|
A |
l |
B |
||
|
|
|
|
|
|
|||
B |
B |
|
B |
|
|
|
|
|
|
|
x |
|
x |
|
x |
||
|
x |
|
x |
|
|
|||
|
а) |
б ) |
|
в) |
г) |
|
|
д ) |
|
|
|
|
Рис. 103 |
|
|
|
|
Пусть r — длина серединного перпендикуляра к отрезку AB от середины отрезка до оси вращения и h — ортогональная проекция отрезка (рис. 104) на
fось вращения. Тогда h = l cos f и r = r cos f, где f — угол наклона отрезка к оси вращения, откуда rl = hr.
A |
A1 Поэтому формуле (7.10) можно придать вид: |
|
|
l |
h |
S = 2prh. |
(7.11) |
|
|
||
rСледовательно, доказанную лемму можно сфор-
f |
мулировать так. |
r |
Следствие. Площадь поверхности, образован- |
|
|
|
ной вращением отрезка около оси, лежащей с ним |
|
в одной плоскости и не пересекающей его во вну- |
B1 |
тренних точках, равна произведению ортогональ- |
B |
ной проекции отрезка на ось и длины окружности, |
x |
|
|
радиус которой равен длине серединного перпендикуляра к отрезку от его середины до оси вращения.
4.2. Объем тела вращения треугольника. Имеет место такая теорема.
Теорема. Объем тела, образованного вращением треугольника около прямой, лежащей в его плоскости, проходящей через его вершину и не содержащей внутренних точек треугольника, равен произведению площади поверхности, полученной вращением противоположной этой вершине стороны, на треть соответствующей ей высоты.
Д о к а з а т е л ь с т в о. Пусть дан треугольник ABC и ось x вращения, удовлетворяющая указанным условиям. Рассмотрим возможные случаи.
1. Сторона AB принадлежит оси вращения (рис. 105). Тогда тело T вращения треугольника представляет собой сумму (или разность) двух
конусов с общим основанием радиуса CE: V (T ) = 13 p · CE2 · AE + 13 p ×
130
