Смольянов. тексты лекция

50

Для расчета теоретических частот по данной формуле составляется вспомогательная ведомость (табл. 6.2).

В 1 и 2 графы этой таблицы записывают средние значения классов и частоты вариационного ряда. В 3 графе вычисляют отклонения «а» средних значений классов (W) от условного начала А в целых интервалах (λ). В 4 графе из отклонений «а», полученных в 3 графе, вычисляют значение первого начального момента ν1, равного в рассматриваемом примере 0,0283. Значение «х» в графе 5 вычисляют

ловных сигмах (σ ). В 6, 7 и 8 графах записывают значение функции нормального распределения f(х), а также третьей и четвертой производной от этой функции - f III (x) и f IV (x). Определяются они по приложению в зависимости от величины «х». При отрицательных значениях «х» знак, указанный в приложении 4, нужно изменить на обратный. Для f(х) и f IV (x) знаки остаются теми же, что и в приложении 3, независимо от знака аргумента. Данные 9 и 10 граф вычисляются по соответствующим формулам, указанным в заголовке граф таблицы 6.2, где : А – коэффициент асимметрии, а Е – коэффициент эксцесса.

В 11 графу записывается сумма чисел 6, 9 и 10 граф. Итоговая сумма цифр 11 графы является контрольной. Она должна быть равна среднеквадратическому

(основному) отклонению, выраженному в интервалах - σ , а в рассматриваемом примере – 2,44.

Теоретические частоты – n в графе 12 – получают путем умножения данных 11 графы на N σ в соответствии с исходной формулой.

52

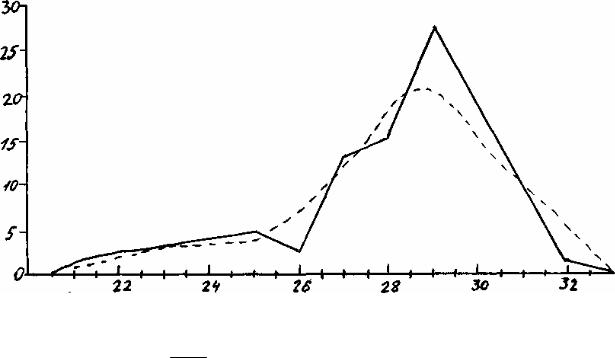
Сумма теоретических частот должна равняться сумме фактических частот вариационного ряда. Результаты проведенного выравнивания в графическом изображении показаны на рис.6.5.

Рис. 6.5 Распределение деревьев дуба по высоте: опытное; ------ теоретическое

Выравниваемые по уравнению А. Шарлье теоретические частоты достаточно хорошо согласуются с опытным распределением, а уравнение А. Шарлье является приемлемой моделью для его характеристики.

4 Распределение редких событий (Пуассона)

До сих пор речь шла о распределениях, хотя и отклоняющихся от нормального, но все же довольно близких к нему. Однако часто встречаются распределения, сильно отличающиеся от нормального.

Важнейшим из них является распределение Пуассона. Если нормальное распределение относится к классу непрерывных распределений и выведено из предположения, что вероятность появления события не очень мала, то распределение Пуассона получается в случае очень малой вероятности события:

Общий член уравнения выражается вероятность P(m), что рассматриваемое событие появится ровно m раз. Подобно нормальному распределению, оно также может быть получено как предельный случай биномиального распределения.

54

вестный в математике предел). Таким образом, окончательно получается вышеприведенная формула распределения Пуассона

Рассмотрим следующий пример. Мешок содержит 100 стаканов белых семян, причем в каждом стакане помещается 100 семян; таким образом, общее число семян равно 10000. Заменим 100 штук белых семян таким же количеством черных. Тогда на каждые 100 семян будет приходиться одно черное семя. Если теперь, после тщательного перемешивания всех семян, зачерпывать из мешка по одной мерке семян, то на каждую порцию придется в среднем одно черное семя. Однако, это вовсе не означает, что на самом деле в каждой порции будет по одному такому семени. В некоторых порциях таких семян не окажется совсем, в других будет по одному семени, в некоторых по два, в каком-то числе порций по три и т.д. Распределение числа порций, в которых окажется то или иное число черных семян, приближенно выражается законом Пуассона. Здесь М – среднее число черных семян в одной порции, равное единице. Тогда число порций, не содержащих черных семян (m = 0), будет:

а число порций, одержащих одно черное семя (m = 1), будет:

55

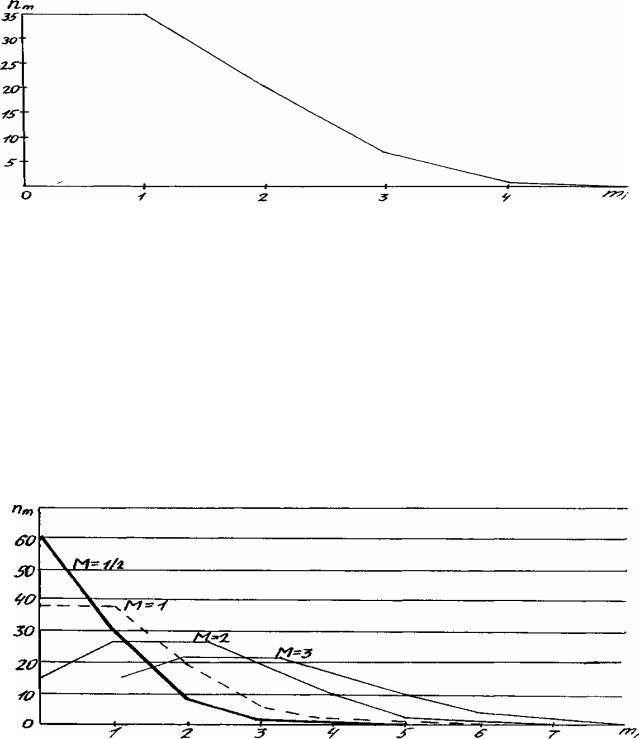
Полигон такого распределения изображен на рис. 6.6.

Рис. 6.6 Полигон распределения опыта с семенами Таким образом, в 37 порциях теоретически не окажется ни одного черно-

го семени, в 37 их будет по одному, в 19 – по два, в 6 порциях – по 3, в одной – 4 черных семени; вероятность появления пяти и более черных семян в одной порции очень мала, так что из таких не окажется ни одной (но в принципе распределение Пуассона распространяется вправо неограниченно).

Формула кривой распределения частот существенно зависит от значения параметра М. В приведенном примере М = 1. Рассмотрим случай, когда М < 1 и М > 1. Вычисленные частоты приведены к объему совокупности N =100. Соответствующие полигоны распределений частот изображены на рис. 6.7.

Рис. 6.7 Полигоны распределения Пуассона при различных значениях Мср

56

Видно, что при М < 1 частоты монотонно убывают с возрастанием m, а при М > 1 имеется максимум; значение М = 1 является в этом отношении критическим. Чем больше М, тем все дальше отодвигается максимум, а симметричность распределения становится все менее и менее заметной. При достаточно больших М распределения мало отличается от симметричного биноминального распределения, близкого к нормальному. Если М > 20, то распределение Пуассона достаточно хорошо приближается к закону Гаусса.

Примечание 2. Расчет моментов распределения Пуассона показывает, что ν1 = М. Далее оказывается, что µ2 = µ3 = М , то есть среднее значение, дисперсия и третий центральный момент равны между собой. Следовательно, если для нормального распределения характерны условия 3 = 0, r4 = 3,то для пуассоновского распределения характерно условие ν 1 = µ 2 = µ 3 . Оно может быть использовано для проверки того, описывается ли данное эмпирическое распределение законом Пуассона или нет.

Распределение Пуассона находит применение в биологии и лесном хозяйстве. Оно, например, описывает распределение численности естественного возобновления древесных пород, когда размер учетных площадок невелик или условия заселения площади подростом неблагоприятны.

Ниже приведены данные учета естественного возобновления сосны на вырубках (размер учетных площадок 1м2). Практическое распределение численности площадок (n) по числу всходов (m) следующее:

Видно, что распределение имеет крайне асимметричный характер, большая часть площадок (329 и 435) не имеет подроста. Малая вероятность появления благоприятного события (наличие подроста) p = М = 0,39 и форма распределения дают основание полагать, что оно соответствует модели Пуассона.

Вычисление выравнивающих частот производится при помощи таблицы значения «Рm» - вероятности появления события «m» (прил. 6), умножая эти значения на численность практического ряда N = 435. Результаты вычислений приведены в последнем столбце табл. 6.3.

57

Таблица 6.3

Распределение числа учетных площадок по количеству естественного возобновления в сосновом древостое

Сравнивая выравнивающие частоты с наблюденными, замечаем сходство характера распределения.

Вопросы для самопроверки:

1 Понятие об асимметрии и крутости рядов распределения. Как используются основные моменты при их оценке?

2 Использование критерия Стьюдента в качественной оценке рядов распределения.

3 Распределение Шарлье и его использование.

4 Техника вычисления теоретических частот по уравнению Шарлье.

5 Распределение Пуассона. Вывод формулы. Практическое использова-

ние.

6 Графическое изображение распределений Шарлье, Пуассона.

58

ЛЕКЦИЯ VII

Статистический анализ выборочных наблюдений

План лекции

1 Задачи статистического анализа наблюдений.

2 Выборочные статистические характеристики оценки параметров.

3 Ошибки выборочных статистических показателей.

4 Критерий Стьюдента, испытание статистических гипотез.

1 Задачи статистического анализа наблюдений

Целью большей части исследований не ограничивается вычислением статистических характеристик выборки. Чаще всего исследователя интересуют статистические характеристики для генеральной совокупности, которые называются параметрами. В случаях, когда теоретические представления могут быть с достаточной определенностью выражены математическими функциями, задача статистического анализа сводится к сопоставлению фактических результатов опыта с теоретически, полученными на основе расчета, а также к оценке степени согласия между ними. Так, теоретическое представление о случайном характере распределения деревьев однородного древостоя по толщине может быть проверено на основе сопоставления экспериментального распределения с теоретической моделью нормального распределения. Для случайных дискретных величин фактические распределения могут быть оценены на основе модели биномиального распределения или распределения Пуассона. Во всех перечисленных случаях статистический анализ производят, пользуясь определенными методами и критериями. Статистические методы и критерии, применяемые для оценки результатов наблюдений, бывают двух видов: параметрические, когда оценка совокупности производится на основе сопоставления параметров распределения (Мср , σ и др.), и непараметрические, когда оценка совокупностей производится на основе непосредственного сопоставления значений варьирующих признаков. Параметрические методы, как опирающиеся на средние величины, наиболее эффективны.

2 Выборочные статистические характеристики оценки параметров

Оценка параметров, т.е. статистических характеристик генеральной совокупности, является центральной задачей статистики. Ранее отмечалось, что оценкой средней величины генеральной совокупности может служить любая,

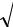
59

случайно взятая варианта. Однако получение точного значения по одной варианте имеет небольшую вероятность. Если мы в качестве оценки генеральной совокупности используем выборочную среднюю, то точность вашего заключения возрастет с увеличением числа наблюдений, на которых основана выборочная средняя.

3 Ошибки выборочных статистических показателей

При рассмотрении среднего квадратического отклонения отмечалось, что его можно рассматривать как меру ошибки выборочной средней, получаемую по одной случайно взятой варианте ряда. Аналогично этому распределении выборочных средних, среднее отклонение их средней величины в генеральной совокупности можно рассматривать как ошибку выборочной средней величины, установленной на основе N наблюдений. Ошибку выборочно средней величины называют также ошибкой репрезентативности. Так как средняя величина вычисляется из некоторого числа вариант, средний квадрат ошибок ее меньше среднего квадрата отклонения отдельных вариант от средней в N раз, т.е.

Выражаются ошибки в тех же единицах измерения, что и отдельные варианты. При статистической характеристике результатов опыта значение средней сопровождается указанием ее ошибки, т.е. результат записывается в форме

Мср ± mM . При толковании ошибки средней величины как среднего квадратического отклонения выборочных средних от генеральной средней необходимо отметить одно свойство, отличающее среднюю ошибку от средней квадратического отклонения. Это свойство состоит в том, что величина средней ошибки mМ уменьшается с увеличением числа наблюдений N, тогда как среднее квадратическое отклонение в этом отношении инертно. Основное свойство средней ошибки связано с действием статистического закона больших чисел, который утверждает, что частость события будет сколько угодно близкой к его вероятности, если число испытаний неограниченно возрастает. Рассматривая выборочную среднюю величину как наиболее вероятную ошибку средней генеральной совокупности, согласно закону больших чисел можно сказать, что при неограниченно возрастающем числе наблюдений различии между этими средними стремится к нулю. Величина средней ошибки зависит не только от объема выборки, но и от величины варьирования признака (чем больше вариация, тем