
Смольянов. тексты лекция
.pdf
10
следующих классов получают путем последовательного прибавления величины интервала. Нижние границы классов определяют путем вычитания половины величины интервала из средних значений каждого класса, а верхние – путем прибавления этой половины. Среднее значение в виде некруглых чисел возможны, так как это не связано с осложнением последующих расчетов. Однако для анализа предпочтительнее иметь ряды распределения с круглыми значениями классов вариант (для диаметра, например, число 16, 20, 24 и т.д.). После того как положение классов установлено, приступают к распределению вариант по классам, помещая каждую в тот или иной класс в соответствии с ее размером. По окончании разноски вариант ряды подсчитывают отдельно для каждого класса, обозначая их числами. Эти числа показывают, как часто встречаются варианты в классах, общее число измерений должно равняться числу измеренных значений признака.
Для последующего статистического анализа результатов наблюдений используют срединные значения классов и значения частот. Полученные таким образом двойные ряды чисел, состоящие из обозначения классов и соответствующих им частот, называют рядами распределения частностей или вариацион-
ными рядами.
16 20 24 28 32 36 40 44 48 52
Рис.1.1 Графическое изображение вариационного ряда:
–полигон распределения;
–гистограмма;
–огива
В целях наглядности вариационные ряды изображаются графически. Если по оси абсцисс отложить значения варьирующего признака (классы), а по оси ординат соответствующие им частоты и точки соединить прямыми линиями, то получим так называемый
многоугольник (полигон) распределения. Вариационный ряд можно представить и в виде ступенчатого многоугольника. Основанием каждого многоугольника будет интервал, а высотой
– частота (рис.1.1). Кривая ряда последовательного суммирования называется огивой. По ней можно определить численное значение любой варианты.
11
Вопросы для самопроверки:
1 Предмет математической статистики в лесном хозяйстве и биологии.
2 Какие методы исследования случайных величин называются случайными?
3 Статистическая совокупность. Понятия, примеры.
4 Этапы статистических обследований.
5 Наблюдения и их признаки. Виды выборок.
6 Группировка результатов. Виды варьирования.
7 Вариационные ряды. Графическое изображение.
ЛЕКЦИЯ II
Статистические показатели распределения частностей
План лекции
1Показатели центральной тенденции. 2 Характеристика выборки.
3 Вычисление статистических показателей распределения.
1Показатели центральной тенденции
Анализ рядов численностей показывает, что в них варианты концентрируются около одного некоторого центрального их значения. Следовательно, можно найти такое среднее значение варианты, которое заменит всю совокупность и будет обладать всеми его свойствами.
В вариационной статистике существует ряд характеристик, показателей центральной тенденции или средних величин: средняя арифметическая, средняя квадратическая, средняя геометрическая, средняя гармоническая, мода и медиана. Тот признак или свойство совокупности, которое остается неизменным при замене индивидуальных значений их средним значением, называется определяющим свойством.
Средняя величина должна отразить определяющее свойство так, чтобы образуемая с ее помощью абстрактная совокупность равных ей чисел по величине определяющего свойства не отличалась от реальной. Из этого требования средней вытекает следующее ее общее определение. Средняя величина - это величина
признака, характеризующая индивидуумы в абстрактной уравненной сово-
12
купности, замещающей их, но при этом сохраняющей неизменным определяющие их свойства.
Например, длину, массу, объем и т.д.
Средняя арифметическая. Это наиболее часто употребляемый статистический показатель центральной тенденции. Она является центром тяжести распределения. Среднюю арифметическую величину генеральной совокупности обо-
_
значают х , а ее выборочную, т.е. среднюю арифметическую величину выборочных наблюдений – Мср. Она имеет то же наименование, что и варианты. Средняя арифметическая для малой выборки (N<25-30) получается от деления суммы всех вариант (V1, V2,… Vn) на их число (N).
Мср |
= |
V1 +V2 +V3 |
+ ... +Vn |
= ∑V |
, |
(2.1) |
N |
|
|||||
|
|
|
N |
|
|
где N – общее число вариант.
Для ряда разделенного на классы, т.е. для вариационного ряда, среднюю арифметическую вычисляют как взвешенную величину:
М ср = |
∑(W n) |
, |
(2.2) |
|
N |
||||
|
|
|
||
где W – среднее значение класса; |
|
|
|
|
n – частоты соответствующих классов; |
|
|
||
N – общее число вариант (объем ряда). |
|
|
||
Основные свойства средней арифметической величины: |
|
|||
1 Сумма отклонений значений ряда от средней арифметической равна нулю. Это свойство вытекает из содержания средней арифметической как центра тяжести ряда. Сумма вариант, которые больше средней, равна сумме вариант, которые меньше ее.
2 Сумма квадратов отклонений отдельных значений ряда от средней величины является наименьшей по сравнению с суммой квадратов отклонений, вычисленной от любой другой величины ряда.
Средняя геометрическая. При изучении среднего темпа роста изучаемого признака средняя арифметическая непригодна. Вместо нее вычисляют сред-
_ |
|
нюю геометрическую Мгеом или х геом |
по формуле |

13 |
|
Мгеом= n V1 V2 V3 ... Vn , |
(2.3) |
где V1, V2, V3,… Vn – темпы роста (величины показывающий во сколько раз увеличивался признак от периода к периоду);
n – число периодов.
Поясняет применение средней геометрической следующий пример: маломерный ствол саженца (сеянца) сосны в конце 1, 2, 3 и 4-й декады роста имел объем в дм3 – 1, 2, 8, 64. Относительный темп прироста объема, как отношение результатов двух последовательных наблюдений, выразится числами 21 = 2, 82 = 4,
648 = 8. В формуле (2.3) они обозначены V1, V2, V3,… Vn. Средняя геометрическая чисел 2, 4, 8 (n = 3) равна
Мгеом=3 2 4 8 = 4.
2 4 8 = 4.
Средняя квадратическая. В лесном хозяйстве нередко приходится находить сумму площадей сечений деревьев в древостое, зная диаметр одного среднего дерева и общее число деревьев. Какую же величину должен представлять диаметр, чтобы он был репрезентативным показателем в указанной цели?
Определяющее свойство – площадь сечений всех деревьев древостоя (G ) выражается формулой
G = (π 4) (n1d12 + n2d22 + ...+ nn dn2 ) , |
(2.4) |
где π = 3,14;
n1, n2, … nn – число деревьев в классах 1, 2, …n; d1, d2, … dn – средние диаметры деревьев в классах.
Очевидно, что G – пропорционально не диаметрам, а их квадратам. Поэтому истинная площадь сечений может быть получена через число деревьев и величину среднего квадратического диаметра.
|
|
|
|
|
|
|
∑ |
(n V |
2 ) |
|
|
Мкв.= |
|
N |
, |
(2.5) |
|
|
|
|
|
|
|
где V2 – квадраты диаметров (или d1, d2, … dn, что применительно к обозначению формулы 2.4);
n – общее число деревьев в классах; N – общее число деревьев в выборке.
Таким образом, для получения истинного значения площади сечений или объемов всех деревьев посредством среднего дерева и числа деревьев, диаметр дерева-модели следует находить как среднюю квадратическую величину. В лес-
14
ной таксации его находят через среднюю арифметическую площадь сечений, что по своей сути то же самое.
Средняя гармоническая. Для вычисления средней характеристики признаков, которые представляют собой отношение двух других варьирующих величин, пользуются средней гармонической. Ее определяют по формуле:
M h |
= |
|
N |
|
, |
(2.6) |
||
|
|
|
|
|||||
∑ |
( |
n |
) |
|||||
|
|
|
|
|||||
|
|
|
||||||
|
|
|
V |
|
|
|
||
где n – вес отдельных значений; N – объем ряда;
V – значения вариант.
Соотношение между рассматриваемыми средними следующее:
Мh < Мгеом < Мср < Мкв .
Мода и медиана. Модой (Мо) называют наиболее часто встречающуюся варианту. При нормальном распределении совокупностей мода равна средней
арифметической. Мода определяется из выражения: |
|
Мо = 3Ме – 2Мср, |
(2.7) |
где Ме – медиана; |
|
Мср – средняя арифметическая величина. |
|
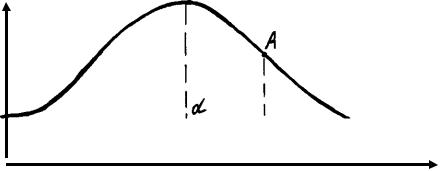
Медианой (Ме) называют значение признака, занимающее среднее положение в ряду и делящее все распределение на две равные по численности части. В большинстве случаев медиана определяется по огиве (рис. 1.1). Мода и медиана являются характеристиками центральной тенденции выборки, но не имеют своего аналога в генеральной совокупности.
2 Характеристика выборки
Средняя величина, являясь показателем центральной тенденции, не дает достаточного представления о свойствах изучаемой совокупности, т.е. она не характеризует степени разнообразия (варьирования) отдельных единиц в этом массиве данных. Если взять, например, два ряда вариант 1, 3, 4, 5, 7 и 3, 4, 4, 4, 5, то они характеризуются одинаковой средней арифметической Мср = 4, но отличаются по степени варьирования значений признака.
Поэтому изучение и характеристика вариации является не менее важной задачей, чем изучение по средней величине. Более того, доверие к самой средней величине может быть определено лишь постольку, поскольку изучена изменчивость признака в статистической совокупности. Если рассеивание настолько ве-

15
лико, что нельзя указать никакой ясно выраженной центральной тенденции, то средняя величина не имеет никакого значения, не заслуживает доверия. Статистические методы, по сути, имеют главной целью изучение вариации явлений и представляют собой набор технологических средств. Наиболее употребляемыми статистическими характеристиками вариации являются размах варьирования, среднеквадратическое отклонение (σ), коэффициент вариации.
Размах варьирования. Размах или разность между наибольшим и наименьшим значением признака является грубым показателем варьирования признака:
Vmax − Vmin = размах варьирования.
Однако этот показатель не учитывает внутреннего варьирования. Кроме того, крайнее значение, как редко встречающийся член ряда, весьма неустойчиво по своему размеру и сильно зависит от объема выборочных наблюдений. Несмотря на это, при малых выборках, повторяемых несколько раз, размах варьирования широко применяется.
Среднеквадратическое отклонение и дисперсия. Основной показатель вариации (изменчивости) – среднеквадратическое отклонение – есть корень квадратный из средней арифметической величины. Среднеквадратическое отклонение для выборочной совокупности обозначают через σ (сигма), а для генеральной совокупности – S.
Согласно определению:
|
|
|
|
|
σ = |
∑(α 2 |
n) |
|
|
N |
, |
(2.8) |
||
|
|
|
|
|
где α – отклонение значений классов от среднего значения (α = W - Мср); n – частота;
N – объем ряда.
Столь же широкое применение в статистике нашел средний квадрат отклонений или среднеквадратическое отклонение (σ2 – для малой и большой выборки и S2 - для генеральной совокупности). Эту величину называют дисперсией. Из формулы (2.8) видно, что она имеет следующее краткое выражение:
σ 2 |
= |
∑(α 2 |
n) |
|
N |
. |
(2.9) |
||
|
|
|
|
Для малой выборки среднеквадратическое отклонение будет:

16
σ = |
∑α 2 |
|
|
N −1 . |
(2.10) |
||
|
Величина (N – 1), применяемая в качестве делителя при малой выборке, называется «числом степеней свободы». Такое название объясняется тем, что в статистике при вычислении любых средних величин используют число независимых величин. При вычислении σ одно из отклонений оказывается свободным. Оно равно сумме всех остальных, взятых с обратным знаком.
Среднеквадратическое отклонение называется также стандартным отклонением, которое выражается в тех же единицах измерения, что и отдельные значения признака.
Свойства среднеквадратического отклонения и дисперсии:
1 При изменении каждой варианты на одну и ту же величину показатели вариации σ и σ2 не меняются.
2 При умножении или делении каждой варианты на одно и то же число К среднеквадратическое отклонение соответственно увеличится или уменьшится в К раз, а дисперсия в К2.
Средняя величина и среднеквадратическое отклонение дают полную количественную характеристику любой эмпирической совокупности, распределяемой по нормальному закону. Средняя арифметическая отображает действие на признак основных факторов, а среднеквадратическое отклонение является мерой степени влияния на причины, вызывающие варьирование. В результате действия этих причин наиболее частыми будут варианты с небольшими отклонениями. Чем отклонения больше, тем варианты встречаются реже, сильнее рассеяны около средней величины. Около 70 % всех вариант отклоняется от средней арифметической не более чем на одну сигму (σ).
Например: средний диаметр 100-летнего соснового насаждения составляет 28,5 см (Мср = 28,5 см), среднеквадратическое отклонение – 6,5 см (σ = 6,5 см), тогда согласно свойству основного (среднеквадратического) отклонения 70% деревьев сосны будут иметь диаметр от 22 см до 35 см.
Коэффициент вариации. Коэффициент вариации (С), как и σ, является
показателем изменчивости признака, выражают его в процентах: |
|
||
С = |
σ |
100 % . |
(2.11) |
|
|||
|
М ср |
|
|
Он является показателем, не зависящим от принятых единиц измерения вариант. Коэффициент вариации может применяться для сравнительной оценки ве-
17
личины варьирования различных признаков. Если коэффициент вариации меньше 10%, то варьирование принято считать малым, от 10 до 30 % – средним, более 30% – высоким. Изучение варьирования лесоводственно-таксационных признаков на множестве объектов позволило сделать по данному вопросу ряд обобщений. Установлено, например, что коэффициент вариации для диаметров деревьев в однородных средневозрастных насаждениях равен 20-25%, для высот – около 10%, для объемов – 40-50%.
3 Вычисление статистических показателей распределения
В зависимости от объема выборки (малая или большая) применяется один из следующих способов вычисления показателей распределения: способ непосредственных вычислений, способ условного начала, способ произведений и способ сумм.
Сущность способа непосредственных вычислений состоит в том, что данные наблюдений относительно какого-либо признака подвергают математической обработке непосредственно без их группировки и составления вариационного ряда. В 1-ом столбце таблицы вписываются значения вариант, во 2-ой столбец – отклонения отдельных значений от их средней арифметической величины. Эти отклонения (α = W – Мср) называют центральными, поскольку средняя арифметическая величина является центром ряда. В 3-ем столбце вписаны квадраты отклонений (α2).
Статистики распределений определяют по формулам 2.1; 2.8 и 2.11.
|
= ∑V |
|
|
σ = |
|
|
|
|
|
Мср |
; |
α = W − Mср ; |
∑ α 2 n |
; |
C = |
σ |
100 . |
||
N |
|
||||||||
|
N |
|
|
|
|
|
M ср . |
||
При использовании способа условного начала можно сказать, что любое условное начало отсчета отклонений вариант будет отстоять от средней арифметической на величину среднего отклонения вариант. Следовательно, задача нахождения средней арифметической величины через условное начало сводится к нахождению средней величины отклонения отдельных вариант от избранного начала А. Обозначив отклонения отдельных вариант V от условного начала А через Vс, можно написать: Vс = V – А. Среднее же отклонение вариант от условного начала (обозначим его К) равно сумме всех отклонений, поделенных на число их или на число наблюдений N, т.е.:
K = |
∑Vc |
. |
(2.12) |
|
N |
||||
|
|
|
18
По данному выше определению средняя арифметическая определяется по выражению:
Мср = А + К . |
(2.13) |
Вопросы для самопроверки:
1 Основные показатели центральной тенденции.
2 Формы средних величин.
3 Средняя арифметическая величина и ее свойства.
4 Мода и медиана, способы нахождения.
5 Основные показатели варьирования.
6 Основное, среднеквадратическое отклонения; свойства.
7 Коэффициент вариации.
8 Способы вычисления статистических показателей.
ЛЕКЦИЯ III
Моменты статистических величин. Их использование в расчетах статистик распределений
План лекции
1 Понятие о статистических моментах.
2Способы вычисления начальных моментов:
2.1Способ произведений.
2.2Способ сумм.
3 Вычисление центральных и основных моментов. Практическое использование моментов.
1 Понятие о статистических моментах
Вычисление статистических показателей Мср и σ способом непосредственных вычислений оказываются весьма громоздкими. Для облегчения вычислительных работ используют моменты ряда, а затем с посредством их вычисляют и статистические показатели.
19
n
W
Рис. 3.1 Статистика моментов, где α – отклонения значений классов (W) от среднеарифметической (Мср), n – частота
Моменты называют начальными, если они вычислялись от условного начала, и центральными, если вычислялись от средней арифметической.
2 Способы вычисления начальных моментов
Начальные моменты обозначают буквой ν (ню) с индексами, указывающими на порядок или степень отклонений: ν0 – нулевой, ν1 – первой, ν2 – второй, ν3 – третьей, ν4 – четвертой степени. Причем ν0 = 1, т.к. все отклонения в нулевой степени равны единице.
2.1 Способ произведений
Для вычисления начальных моментов по этому способу используются следующие формулы:
ν 1 |
= |
∑(аn) |
; ν 2 |
= |
∑(a2 n) |
; ν 3 |
= |
∑(a |
3 n) |
; |
ν 4 = |
∑(a4 n) |
, (3.1) |
N |
N |
N |
|
N |
|||||||||
|
|
|
|
|
|
|
|
|
|
где а, а2, а3, а4 – отклонения классов от среднего значения, выраженное в условных единицах.
Условные единицы определяются по формуле: a = |
W − A |
, |
(3.2) |
|
λ |
||||
|
|
|
где W – среднее значение класса;
A – произвольное начало; λ – величина интервала.
Для центрального класса условное отклонение равно нулю, так среднее значение класса и произвольное начало A здесь равны. Начиная расчет отклонений от центрального класса, получим для классов, находящихся в стороне значений вариант меньших A, натуральный ряд чисел со знаком минус (–1, –2, –3, –4 и т.
