
Смольянов. тексты лекция
.pdf40
Таблица 5.4 Вычисление теоретических частот по таблице площади нормальной кривой
|
|
|
Отклоне- |
|
|
|
Кол-во |
|
Среднее |
Пределы |
Средняя |
Отклоне- |
Кол-во ва- |
Кол-во |
вариант |
||
значение |
арифм. |
ние пре- |
ние пре- |
риант от М |
вариант |
в клас- |
||
классов, |
делов |
|||||||
классов, |
величина, |
делов от |
до пределов |
в клас- |
се, в |
|||
см |
см |
см |
классов |
М в σ |
классов, % |
се, % |
абс. |
|
|
от М, см |
|||||||
|
|
|
|
|
|
цифрах |
||
|
|
|
|
|
|
|
||
|
6 |
|
-25,4 |
-3,68 |
50,0 |
|
|
|
8 |
|
|
|
|
|
0,1 |
0,2 |
|
|
10 |
|
-21,4 |
-3,10 |
49,9 |
|
|
|
12 |
|
|
|
|
|
0,5 |
1,0 |
|
|
14 |
|
-17,4 |
-2,52 |
49,4 |
|
|
|
16 |
|
|
|
|
|
2,0 |
4,2 |
|
|
18 |
|
-13,4 |
-1,94 |
47,4 |
|
|
|
20 |
|
|
|
|
|
6,1 |
12,7 |
|
|
22 |
|
-9,4 |
-1,36 |
41,3 |
|
|
|
24 |
|
|
|
|
|
13,1 |
27,2 |
|
|
26 |
|
-5,4 |
-0,78 |
28,2 |
|
|
|
28 |
|
|
|
|
|
20,3 |
42,2 |
|
|
30 |
31,4 |
-1,4 |
-0,20 |
7,9 |
|
|
|
32 |
|
|
|
|
|
22,7 |
47,3 |
|
|
34 |
|
+ 2,6 |
+ 0,31 |
14,8 |
|
|
|
36 |
|
|
|
|
|
18,3 |
38,1 |
|
|
38 |
|
+ 6,6 |
+ 0,96 |
33,1 |
|
|
|
40 |
|
|
|
|
|
10,7 |
22,2 |
|
|
42 |
|
+ 10,6 |
+ 1,54 |
43,8 |
|
|
|
44 |
|
|
|
|
|
4,5 |
9,3 |
|
|
46 |
|
+ 14,6 |
+ 2,12 |
48,3 |
|
|
|
48 |
|
|
|
|
|
1,4 |
2,8 |
|
|
50 |
|
+ 18,6 |
+ 2,70 |
49,7 |
|
|
|
52 |
|
|
|
|
|
0,2 |
0,6 |
|
|
54 |
|
+ 22,6 |
+ 3,28 |
49,9 |
|
|
|
56 |
|
|
|
|
|
0,1 |
0,2 |
|
|
58 |
|
+ 26,6 |
+ 3,86 |
50,0 |
|
|
|
ИТОГО |
|
|
|
|
|
100 |
208,0 |
Вопросы для самопроверки:
1 Виды теоретических распределений (моделей).
2 Биномиальное распределение. Основные статистики. Практическое применение.
3 Треугольник Паскаля. Применение при практическом моделировании.
4 Нормальное распределение. Уравнение.
5 Свойства кривой нормального распределения.
41
6 Вычисление теоретических частот по таблице ординат нормальной кривой.
7 Вычисление теоретических частот по таблице площади нормальной кривой.
ЛЕКЦИЯ VI
Асимметричные распределения
План лекции
1 Асимметрия и крутость рядов распределений.
2 Двухвершинные и другие виды распределений.
3 Распределение Шарлье (тип А).
4 Распределение редких событий (Пуассона).
1 Асимметрия и крутость рядов распределения
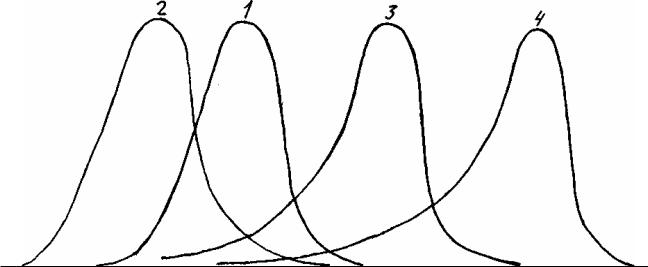
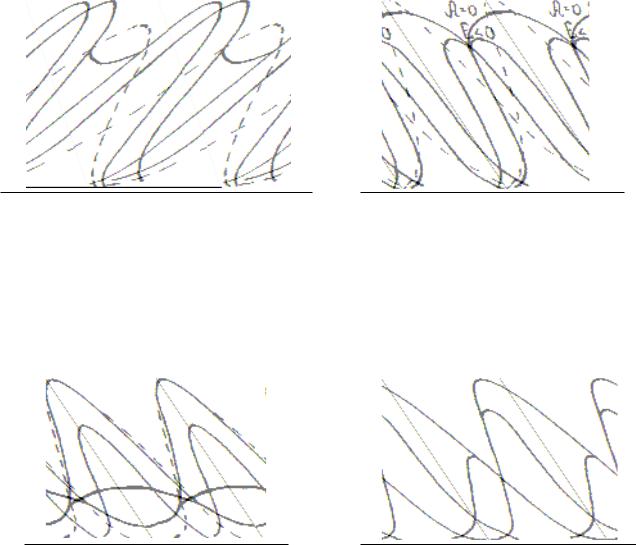
Кривая теоретического (нормального) распределения представляет собой кривую, симметричную относительно оси ОУ: средняя арифметическая величина, медиана и мода совпадают, а правая ветвь кривой является зеркальным отображением левой. Кривые практических рядов такой правильности не имеют. Не вдаваясь пока в исследование причин этого свойства (это свойство принято называть асимметрией), рассмотрим каким образом можно дать его количественные описания. Степень асимметрии может быть различной (рис. 6.1).
Рис. 6.1 Асимметрия кривых: 1 – нормальная кривая; 2 – кривая с правой асимметрией; 3 – кривая с меньшей левой асимметрией; 4 – кривая с большей левой асимметрией

42
Нужно найти такой параметр, который являлся бы количественной характеристикой асимметрии.
Вычислим средний куб отклонения отдельных вариант от среднего значе-
ния:
α 3 |
= |
1 |
= |
1 |
|
. |
(6.1) |
|||
|
|
|
|
|||||||
N ∑α i3 |
N ∑ (Vi |
− M )3 |
||||||||
В отличие от среднего отклонения |
α = |
|
1 |
, которое, как это было |
||||||
|
|
|||||||||
N ∑αi |
||||||||||
|
|
|
|
|
|
|
|
|||
показано выше, равно нулю, средний куб отклонения в общем случае отличен от нуля. Действительно, пусть некоторое любое заданное распределение содержит, помимо прочих, отклонения α1 = –5 с частотой n1 = 12 и α2 = 2 с частотой n2 = 30.
При |
вычислении α |
отвечающие |
этим |
классам слагаемые будут равны: |
|||
n1α1 |
= 12 (− 5)= −60 и n2α 2 = 30 2 = 60 , так что они компенсируются. |
||||||
|
В то же время при вычислении |
α3 |
соответствующие слагаемые будут |
||||
равны:n α 3 = 12 (−125)= −1500 и n |
2 |
α |
3 = 30 8 = 240 , а компенсации не будет. |
||||
|
1 |
1 |
|
|
2 |
|
|
Величина равна нулю в том случае, если распределение симметрично: так как при таком распределении расположение симметрично (по отношению к центру распределения) частоты, равные по величине, но противоположные по знаку (ибо
значение возводятся в нечетную степень) слагаемые в сумме ∑niαi3 .
Очевидно, величина  α3
α3  тем больше, чем сильнее выражена асимметрия
тем больше, чем сильнее выражена асимметрия
распределения. Кроме того, знак величины  α3
α3  («+» или «–») однозначно связан с направлением асимметрии: если распределение вытянуто в сторону положительных значений (центр распределения принимаем за нуль), то
(«+» или «–») однозначно связан с направлением асимметрии: если распределение вытянуто в сторону положительных значений (центр распределения принимаем за нуль), то  α3
α3  >0; в про-
>0; в про-
тивном случае  α3
α3  < 0.
< 0.
По этим причинам естественно принять  α3
α3  в качестве характеристики асим-
в качестве характеристики асим-
метрии распределения. Однако численное значение характеристики асимметрии не должно меняться при изменении масштаба изменения величин. Это условие будет со-
блюдено, если разделить  α3
α3  на σ 3 . В итоге получим параметр, называемый
на σ 3 . В итоге получим параметр, называемый

43
 α 3
α 3 
коэффициентом асимметрии А = σ 3 , который будет безразмерным.
В статистических моментах коэффициент асимметрии запишется так:
А = |
µ |
3 |
= |
|
µ |
3 |
|
= r3 . |
(6.2) |
|
|
|
|
|
|
||||||
σ |
3 |
( |
|
|
)3 |
|||||
µ |
2 |
|||||||||
Следует иметь в виду, что значение коэффициента А является более существенным показателем асимметрии, чем вид графика распределения (дело в том, что форма графика распределения в определенной мере зависит от способа группировки вариант по классам).
Для оценки величины асимметрии применяются следующие придержки:
А< ±0,5 – асимметрия считается малой;
А= ±0,5 ÷ 1,0 – асимметрия средняя;
А> ±1,0 – асимметрия большая.
Знак плюс «+» характеризует правую, а знак минус «–» левую асимметрию. Для вариационного ряда, использованного в качестве примера, третий основной момент r3 = +0,25. Следовательно, рассматриваемая кривая имеет малую положительную (правую) асимметрию.
Показатель эксцесса (крутость). Критерием отклонения практического распределения от нормального может служить отклонение r3 от значения r3 = 0, отвечающего нормальному распределению.
Однако выполнение условия r3 = 0 еще не означает, что распределение нормально. Дело в том, что для нормального распределения характерно не только равенство нулю всех нечетных основных моментов (вследствие симметричности этого распределения), но и вполне определенные значения четных основных моментов; в частности, для нормального распределения свойственно равенство r4 = 3.
Поэтому, если r4 эмпирического распределения заметно отличается от 3, то такое распределение не может считаться нормальным, даже если оно симметрично.
Выясним, какой смысл имеет то обстоятельство, что r4 равен не 3, а больше или меньше этой величины. Для этого сравним три симметричных распределения с одинаковыми объемами выборки N, средними значениями М
и стандартными отклонениями σ, но с
Рис. 6.2 Эксцессы кривых: различными r4. Одно из этих распреде- 1 - нормальная; 2 – островершинная;
лений является нормальным, так что 3 - плосковершинная
44
для него r4 = 3, для второго r4 > 3 и для третьего r4 < 3.
Эти три распределения изображены на рис. 6.2.
При r4 > 3 кривая называется островершинной (высоковершинной), а при r4 < 3 – туповершинной. Вообще же свойство кривой, отображаемое значением r4, называют эксцессом кривой. Обычно эксцесс кривой распределения характеризуют не значением r4, а отклонением его от нормального значения при r4норм = 3.
Величина Е = r4 - 3 называется коэффициентом эксцесса.
В нормальном распределении только 3 наблюдения (варианты) из 1000 лежат вне пределов утроенного стандартного отклонения (0,03%) в ту или другую стороны от средней величины. При Е > 0 (r4 > 3) за эти пределы выходит большее число единиц совокупности; такое явление (эксцесс) сопровождается большой крутизной кривой, т.е. большим скоплением вариант около М, чем в нормальном распределении (рис.6.2). Если варианты расположены в более узких пределах, чем
М ± 3σ , то это явление называют дефектом (отрицательный эксцесс). Кривая оказывается плосковершинной.
Теоретически установлено, что отрицательные коэффициенты эксцесса имеют нижнюю границу Е ≥ 2 (т.е. r4 не может быть меньше единицы), а положительный эксцесс может иметь любые значения.
2 Двухвершинные и другие виды распределений
При изучении лесоводственных явлений иногда встречаются распределения, которые по форме значительно отличаются от нормальной кривой. К ним, в частности, относятся двух-, многовершинные и односторонние кривые. При анализе подобных распределений, характеризующихся указанными кривыми, следует выяснить причину их возникновения.
Рассмотрим некоторые причины, приводящие к отклонению эмпирического распределения от нормального. Одной из причин этого может быть то, что совокупность является неоднородной. Последнее означает, что в одну совокупность сведены две или большее число совокупностей, каждая из которых характеризуется своим набором основных параметров N, M и σ и может подчиняться закону нормального распределения. Так если мы будем строить распределения по массе группы студентов без различия пола, то заведомо не получится нормальное распределение, даже если для каждой из совокупностей – отдельно для юношей и де-
45
вушек – распределение является нормальным. Та же картина наблюдается при анализе распределения диаметров деревьев в разновозрастном древостое ели. При детальном рассмотрении все деревья можно отнести к двум возрастным группам (поколениям) – 120 и 70 лет. Общее распределение существенно отличается от нормального, хотя каждое поколение в отдельности можно охарактеризовать нормальным распределением.
Если разница между средними значениями двух подсовокупностей больше, чем стандартное отклонение каждой из них, то кривая распределения будет двухвершинной (рис.6.3, А); при небольшом различии средних значений кривая имеет одну, но тупую вершину (рис.6.3, Б).
А) |
Б) |
Рис. 6.3 Кривые распределений: А – двухвершинная, Б – туповершинная (жирные линии – графики распределения суммарных неоднородных совокупностей; пунктирные линии – графики нормальных совокупностей)
На рис.6.4 представлены два других частных случая, приводящих к «аномальному» распределению.
А) |
Б) |
||
|
А=0 |
|
А≠0 |
|
Е >0 |
|
|
|
|
|
|
Рис 6.4 «Аномальное» распределение:
А – высокий положительный эксцесс; Б – правосторонняя асимметрия
46
Суммарное распределение (как результат смешения двух совокупностей) в первом случае характеризуется высоким положительным эксцессом, во втором – правосторонней асимметрией. Разумеется, сводить в одну статистическую совокупность мужчин и женщин нецелесообразно.
Исследование разновозрастного древостоя также обычно проводится с разделением на возрастные поколения. Но вполне возможны случаи, когда в исследуемую совокупность попадают экземпляры различного происхождения или развившиеся в разных условиях, или подвергшиеся специфическим внешним воздействиям. Так при исследовании выборки желудей в ней могут оказаться экземпляры, значительно отличающиеся по весу и размерам вследствие существенного различия условий материнских деревьев и локального воздействия в пологе древостоя вредителей-насекомых.
В связи с этим отклонением распределения от нормального обычно наталкивает на мысль о том, что совокупность не является однородной. Однако, неоднородность совокупности – лишь одна из возможных причин отклонений распределения от нормального. Вопрос об однородности или неоднородности заданной статистикой совокупности может быть решен окончательно только на основе биологического анализа исследуемого объекта.
3 Распределение Шарлье
Как правило, опытные распределения имеют ту или иную степень асимметрии или эксцесса. Если эти показатели оказываются больше критических значений, выравнивание опытных вариационных рядов по нормальному закону производить не рекомендуется. В этих случаях целесообразнее воспользоваться уравнением А. Шарлье, учитывающим асимметрию и эксцесс опытных рядов.
В качестве примера для вычисления теоретических частот по уравнению А. Шарлье возьмем данные обмера высот деревьев в культурах дуба Шипова леса (табл. 6.1).
Для данного вариационного ряда необходимо решить вопрос о характере распределения деревьев по высоте, т.е. нужно подобрать соответствующую теоретическую модель и оценить степень соответствия вариационного ряда этой модели.
Первоначально выдвигается нулевая гипотеза об отсутствии различий между данным распределением и нормальным.
47
|
|
|
|
|
|
Таблица 6.1 |
|
|
|
Результаты обмера высот культур дуба, м |
|
|
|||
|
|
|
|
|
|
|
|
20,7 |
25,4 |
27,4 |
28,5 |
29,0 |
29,8 |
30,7 |
|
20,9 |
26,0 |
27,5 |
28,6 |
29,0 |
29,8 |
30,7 |
|
22,0 |
26,1 |
27,6 |
28,6 |
29,1 |
29,9 |
30,8 |
|
22,1 |
26,3 |
27,7 |
28,7 |
29,1 |
29,9 |
30,9 |
|
22,4 |
26,6 |
27,7 |
28,7 |
29,1 |
30,0 |
30,9 |
|
22,6 |
26,7 |
27,8 |
28,7 |
29,2 |
30,0 |
31,0 |
|
22,8 |
26,7 |
27,9 |
28,8 |
29,2 |
30,0 |
31,0 |
|
23,1 |
26,8 |
28,0 |
28,8 |
29,3 |
30,1 |
31,0 |
|
23,7 |
26,9 |
28,0 |
28,9 |
29,4 |
30,2 |
31,3 |
|
23,9 |
26,9 |
28,0 |
28,9 |
29,5 |
30,2 |
31,8 |
|
24,0 |
26,9 |
28,1 |
28,9 |
29,5 |
30,2 |
|
|
24,4 |
27,0 |
28,1 |
29,0 |
29,6 |
30,3 |
|
|
24,7 |
27,0 |
28,1 |
29,0 |
29,6 |
30,4 |
|
|
24,8 |
27,0 |
28,2 |
29,0 |
29,6 |
30,5 |
|
|
25,0 |
27,1 |
28,4 |
29,0 |
29,7 |
30,6 |
|
|
25,0 |
27,2 |
28,4 |
29,0 |
29,7 |
30,6 |
|
|
Для проверки этой гипотезы необходимо сделать оценку степени асимметрии (косости) и эксцесса (крутости) исследуемого вариационного ряда по сравнению с нормальным. С этой целью предварительно вычисляются начальные, центральные и основные моменты.
Средние значения |
|
|
|
|
21 |
|
|
22 |
23 |
24 |
|
25 |
26 |
27 |
28 |
29 |
|
30 |
|
|
31 |
32 |
||||||
классов высоты, м (W) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Частоты (число |
|
|
|
|
2 |
|
|
3 |
3 |
4 |
|
5 |
3 |
14 |
15 |
26 |
|
19 |
|
|
11 |
1 |
||||||
деревьев), шт. (n) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Вычисление начальных моментов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ν1 |
= |
∑аn |
= |
|
|
3 |
|
= 0,0283; |
|
|
|
ν 3 |
= |
∑a3 n |
= |
|
− 1599 |
|
= −15,1; |
|||||||||
N |
106 |
|
|
|
|
|
N |
|
|
106 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ν2 |
= |
∑a2n |
= |
|
633 |
= 5,97; |
|
|
|
ν 4 |
= |
∑a4 n |
= |
13533 |
|
= 127,7. |
||||||||||||
|
|
106 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
N |
|
|
|
|
|
N |
|
|
106 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

48
Вспомогательные расчеты для вычисления начальных моментов
W |
n |
а* |
|
|
аn |
|
а2 |
а2n |
а3 |
а3n |
а4 |
а4n |
21 |
2 |
-7 |
|
-14 |
|
49 |
98 |
-343 |
-686 |
2401 |
4802 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
3 |
-6 |
|
-18 |
|
36 |
108 |
-216 |
-648 |
1296 |
3888 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
3 |
-5 |
|
-15 |
|
25 |
75 |
-125 |
-375 |
625 |
1875 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
4 |
-4 |
|
-16 |
|
16 |
64 |
-64 |
-256 |
256 |
1024 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
5 |
-3 |
|
-15 |
|
9 |
45 |
-27 |
-135 |
81 |
405 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
3 |
-2 |
|
-6 |
|
4 |
12 |
-8 |
-24 |
16 |
48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
14 |
-1 |
|
-14 |
|
1 |
14 |
-1 |
-14 |
1 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А=28 |
15 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
29 |
26 |
1 |
|
26 |
|
1 |
26 |
1 |
26 |
1 |
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
19 |
2 |
|
38 |
|
4 |
76 |
8 |
152 |
16 |
304 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
11 |
3 |
|
33 |
|
9 |
99 |
27 |
297 |
81 |
891 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
1 |
4 |
|
4 |
|
16 |
16 |
64 |
64 |
256 |
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-98 |
|
|
|
|
-2138 |
|
|
|
Итого |
106 |
|
|
+ 101 |
|
|
633 |
|
+ 539 |
|
13533 |
|
|
|
|
|
+ 3 |
|
|
|
|
-1599 |
|
|
|
Примечание: а* – a = |
W − A |
, |
где: λ – величина интервала между классами. |
|
||||||||
|
λ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление центральных моментов:
µ2 |
=ν 2 |
−ν12 = 5,973− 0,02832 |
= 5,97 |
||||||
µ |
3 |
=ν |
3 |
− 3ν ν |
1 |
+ 2ν 3 |
= −15,1− 3 5,97 0,0283+ 2 0,02833 = −15,6 |
||
|
|
2 |
1 |
|
|
|
|||
µ |
4 |
=ν |
4 |
− 4ν ν |
1 |
+ 6ν ν 2 |
− 3ν 4 |
= |
|
|
|
3 |
2 |
1 |
1 |
|
|||
= 127,7 − 4 (−15,1) 0,0283+ 6 5,97 0,02832 − 3 0,02834 = 129,44
Вычисление основных моментов:
r3 = |
|
3 |
|
= −1,07; |
r4 = |
|
4 |
|
= 3,63. |
( |
|
)3 |
( |
|
)4 |
||||
2 |
2 |
Показатель асимметрии вариационного ряда:
A = r3 = −1,07 .
Ошибка показателя асимметрии:
m |
|
= ± |
|
6 |
|
= ± |
|
6 |
|
= 0,238 . |
|
A |
N |
106 |
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
Показатель эксцесса вариационного ряда:
E = r4 − 3 = 3,54 − 3 = 0,63.
49
Ошибка показателя эксцесса:
m E |
= |
|
24 |
|
= |
|
24 |
|
= 0,476 . |
|
106 |
||||||||
|
|
|
N |
|
|
||||
Оценка степени асимметрии и эксцесса вариационного ряда производится с помощью критерия Стьюдента. Вначале вычисляются фактическое значение критерия для коэффициента косости – tА и коэффициента эксцесса – tЕ.
t A |
= |
A |
= 4,5 |
tE |
= |
E |
= 1,32 . |
|
|
||||||
|
|
m A |
|
|
mE |
||
Полученные фактические значения tА и tЕ сравниваются со стандартным значением этого критерия - tst, которое определяется по приложению 3.
Для рассматриваемого примера, при числе степеней свободы f = n−1=106−1=105, tst для вероятностей 0,95; 0,99; 0,999 равно 1,98; 2,62; 3,37. Так как tА = 4,5 > tst = 3,37, можно сделать вывод, что исследуемый вариационный ряд высот по степени асимметрии (косости) существенно отличается от нормального ряда. Нулевая гипотеза отвергается. Для показателя эксцесса (крутости) такой вывод сделать нельзя, т.к. tЕ = 1,32 < tst = 1,98. Следовательно, имеющиеся отклонения в крутости исследуемого ряда от нормального является случайным. Нулевая гипотеза сохраняется.
Наличие существенной асимметрии исследуемого вариационного ряда (К = –1,07) свидетельствует о том, что производит выравнивание частот по уравнению нормальной кривой нельзя.
Теоретические частоты для кривой Шарлье типа «А» вычисляются по следующему уравнению:
|
= |
|
N |
|
|
f (x ) − |
A |
f III (x ) + |
E |
|
IV (x ) |
, |
(6.3) |
|
n |
f |
|||||||||||||
|
|
|
|
|
|
|||||||||
|
|
σ |
|
|
σ |
24 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
где n – теоретические частоты;
f (x ) – функция нормального распределения;
fIII (x ), f IV (x ) – третья и четвертая производные функции нормального
распределения; А – показатель асимметрии (косости) ряда;
Е – показатель эксцесса (крутости) ряда; х – нормальное отклонение средних значений классов от среднего значе-
ния признака;
N – численность ряда;
σ – среднеквадратическое отклонение в единицах интервала σ = σ λ .
