
Смольянов. тексты лекция
.pdf
30
p = q = 12 .
Так происходит при бросании монеты. Пусть мы бросили одновременно две монеты. Подсчет вероятностей показывает: вероятность выпадения двух «гербов» равна 14 , вероятность выпадения двух «цифр» – 14 , выпадения «герба» на пер-
вой монете, а «цифры» на второй – 14 и наоборот – то же 14 . Если не учитывать номера монет, то вероятность выпадения разного рисунка на монетах будет составлять 12 . Или на схеме:
pp − |
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pq − 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
4 |
|
1 |
|
+ |
1 |
|
= |
1 |
|
qp − |
1 |
|
|
4 |
4 |
2 |
||||||
4 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
qq − |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В сумме В(p, q) = 14 + 12 + 14 = 1.
В случае бросания трех монет вероятности распределятся следующим образом, если не учитывать номера монет: ppp, ppq, pqq, qqq, или:
18 + 38 + 38 + 18 = 1.
При бросании двух и трех монет соответственно 4 и 8 раз теоретическая частота появления результатов получится соответственно:
1 – 2 – 1 |
и |
1 – 3 – 3 – 1 |
Если сопоставить эти и другие данные (в случае бросания большого количества монет), то видно, что частоты соответствуют коэффициентам разложения бинома Ньютона:
|
|
(p + q)n , |
(5.1) |
где p – вероятность ожидаемого события (благоприятного исхода); |
|||
|
q = (1 - p) – вероятность противоположного события. |
||
Так, |
(p + q)2 |
= 1p2 + 2 pq +1q2 |
(5.2) и так далее. |
(p + q)3 |
= 1p3 + 3p2q + 3pq2 +1q3 |
||
В общем виде формула для вероятности того, что при одновременном бросании «n» монет «герб» выпадает на каких-нибудь «m» монетах, будет:
p = cnm qm pn−m . |
(5.3) |

31
Суммирование по всем возможным значениям «m» (от 0 до n) должно дать
полную вероятность, т.е.
∑ cnm q m p n−m = 1. 1.
(5.4)
Эта сумма есть не что иное, как развернутая формула бинома Ньютона:
|
(p + q)n |
= ∑cnm qm pn−m . |
(5.5) |
||
Для определения частот биномиального распределения используется фор- |
|||||
мула Бернулли: |
n |
= Ncm pmqn−m |
. |
(5.6) |
|
m |
n |
|
|||
Она показывает, что если произведено «N» серий по «n» испытаний в каждом, то следует ожидать, что число серий испытаний с «m» благоприятными исходами (вероятность такого исхода - p) будет близко «nm».
Например, если 1000 раз бросить горсть из 8 монет, то число бросаний, в которых герб выпадет на трех монетах из восьми, должно быть близко
n |
|
= 1000 |
8! |
|
( 1 |
)3 ( 1 )8−3 |
|
3 |
|
|
|
||||
|
|
|
|||||
|
|
3!(8 |
− 3)! |
2 |
2 |
||
|
|
|
|||||
где ! – факториал числа.
Биномиальное распределение определяется
– средней величиной:
M = n p ;
– дисперсией:
= 1000 81 27 36 218 = 219 ,
двумя параметрами:
(5.7)
σ 2 = n p q |
(5.8) |
или среднеквадратическим отклонением:
|
|
|
|
σ = n p q . |
(5.9) |
||
Для рассматриваемого примера имеем среднюю частоту появления «герба» на 8 монетах:
M = np = 8 12 = 4
и дисперсию:
σ 2 = npq= 8 12 12 = 2.
Значительно облегчает нахождение биномиальных коэффициентов при разных «n» так называемый треугольник Паскаля (табл. 5.1).
32
Таблица 5.1
Треугольник Паскаля
|
|
|
|
|
|
|
|
|
|
|||
n |
|
|
|
Биномиальные коэффициенты |
|
|
|
N+1 |
N=2n |
|||
0 |
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|
|
2 |
2 |
2 |
|
|
|
1 |
2 |
1 |
|
|
|
|
3 |
4 |
3 |
|
|
|
1 |
3 |
3 |
1 |
|
|
|
4 |
8 |
4 |
|
|
1 |
4 |
6 |
4 |
1 |
|
|
|
5 |
16 |
5 |
|
|
1 |
5 |
10 |
10 |
5 |
1 |
|
|
6 |
32 |
6 |
|
1 |
6 |
15 |
20 |
15 |
6 |
|
1 |
|
7 |
64 |
7 |
|
1 |
7 |
21 |
35 |
35 |
21 |
7 |
1 |
|
8 |
128 |
8 |
1 |
8 |
28 |
56 |
70 |
56 |
28 |
|
8 |
1 |
9 |
256 |
Каждый коэффициент образуется сложением двух, стоящих над ним (слева и справа), коэффициентов; например, 3 = 2 + 1; 15 = 5 + 10; 84 = 28 + 56 и т.д.
Пользуясь этим правилом, можно продолжить треугольник Паскаля до нужного значения.
Можно ли по коэффициентам разложения бинома построить теоретический вариационный ряд? Оказывается можно. Для этого порядковые номера коэффициентов следует принять за средние значения классов, а сами коэффициенты – за частоты.
Возьмем, например, бином в шестой степени (p+q)6. Коэффициентами разложения такого бинома будут (табл. 5.1):
1 – 6 – 15 – 20 – 15 – 6 – 1.
Тогда:
Средние значение классов (W) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Частоты (n) |
1 |
6 |
15 |
20 |
15 |
6 |
1 |
Частности, % |
1,6 |
9,4 |
23,4 |
31,2 |
23,4 |
9,4 |
1,6 |
Графически ряд распределения представлен на рис. 5.1. n
20 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
5 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
W |
Рис. 5.1 Распределение теоретических частот (W=7, N=64)
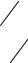
33
Среднее значение такого распределения М = 4, а среднеквадратическое отклонение σ2 = 1,5. Этими данными теоретического распределения можно, например, описать частоты (вероятности) выпадения «гербов» при бросании 6 монет 64 раза. Так, исход без появления «герба» (среднее значение класса – 1) будет наблюдаться 1 раз (вероятность – 164 ), «герба» на одной монете (среднее значение
класса – 2) – 6 раз (вероятность – 664 ) и т.д.
Рассмотрим еще один пример. Сравним теоретическое распределение мужских особей майского хруща с практическим их количеством в 80 выборках по 12 насекомых в каждом. Так, в одной выборке совсем не было мужских особей (число равно нулю), в 6 выборках было по 3 особи, в 16 выборках – по 7 мужских особей и т.д.
Данные теоретического распределения приведены в табл. 5.2.
Таблица 5.2 Сравнение теоретического распределения мужских особей майского хруща
с фактическим их количеством в выборках
Число мужских |
Фактическое число |
Биномиальные |
Теоретическое |
особей |
выборок |
коэффициенты |
число выборок |
|
|
|
|
0 |
1 |
1 |
0,0 |
|
|
|
|
1 |
0 |
12 |
0,2 |
|
|
|
|
2 |
0 |
66 |
1,3 |
|
|
|
|
3 |
6 |
220 |
4,3 |
|
|
|
|
4 |
11 |
495 |
9,7 |
|
|
|
|
5 |
13 |
792 |
15,5 |
|
|
|
|
6 |
19 |
924 |
18,0 |
|
|
|
|
7 |
16 |
792 |
15,5 |
|
|
|
|
8 |
7 |
495 |
9,7 |
|
|
|
|
9 |
4 |
220 |
4,3 |
|
|
|
|
10 |
2 |
66 |
1,3 |
|
|
|
|
11 |
1 |
12 |
0,2 |
|
|
|
|
12 |
0 |
1 |
0,0 |
|
|
|
|
Сумма |
80 |
4096 |
80 |
|
|
|
|
Посмотрим, можно ли это распределение считать биномиальным. Для этого по формуле Бернулли или из треугольника Паскаля (формула (5.6) или табл. 5.1) необходимо найти биномиальные коэффициенты для разных «m» при «n» = 12.
34
Например:
с123 |
= |
12 11 10 |
= 220 ; |
||||
|
1 2 3 |
||||||
|
|
|
|
|
|||
п |
|
= |
80 220 |
= 4,3 . |
|||
3 |
4096 |
||||||
|
|
|
|
||||
|
|
|
|
|
|||
Значения с12m и nm записаны соответственно в 3 и 4 колонках таблицы 5.2;
значение «nm» получены умножением « с12m » на постоянный множитель:
Пмн = N (12)12−m (12)m = 2N12 = 409680 = 0,0195.
Сравнивая теоретические и эмпирические частоты, видим, что хотя соответствие является довольно относительным, общий характер распределения передается все же верно. Определенные критерии оценки степени совпадения будут изложены в следующих разделах.
Предельным случаем биномиального распределения, когда число наблюдений (испытаний) неограниченно возрастает, является нормальное распределение (рис. 5.2)
А) |
n=6 |
|
|
|
Б) |
|
n=20 |
В)
n  ∞
∞
Рис. 5.2 Распределение коэффициентов бинома различной степени: А) n = 6; Б) n = 20; В) n → ∞

35
2 Нормальное распределение
Уравнение кривой нормального распределения (распределение Гаусса) име-
ет вид: |
y = |
|
N |
|
e х 2 |
2 σ 2 |
, |
(5.10) |
|
|
|
|
|
||||||
|
2π |
|
|||||||
|
σ |
|
|
|
|
|
|
||
где y – частота; N – объем ряда (сумма частот); σ – основное отклонение; е – основание натуральных логарифмов;
х – отклонение от среднего значения: х = W – М.
При выражении отклонений в долях σ, если принять σ =1, (т.е. x = W − M )
σ
уравнение примет вид:
y = |
|
1 |
|
e х 2 |
2 |
(5.11) |
|
|
|
||||
2π |
|
|||||
|
|
|
|
|
|
|
и будет иметь максимальное значение ymax =0,39 |
при аргументе, равном 0. |
|||||
Такой вид нормального распределения показывает вероятность появления того или иного отклонения от среднего значения. Поэтому ее называют кривой вероятностей. Очевидно, что максимальную вероятность 0,39 имеют величины, равные среднему значению. При отклонении величин от средней вероятность их появления уменьшается; с увеличением до 3–3,5 σ отклонения она приближается к 0.
Площадь, ограниченная такой кривой, равна 1 и характеризует плотность
вероятности: |
y= |
|
1 |
|
∫eх2 |
2 dx. |
(5.12) |
|
|
|
|
||||||
2π |
||||||||
|
|
|
|
|
|
|
Результаты анализа уравнения кривой нормального распределения позволяют сделать следующие заключения:
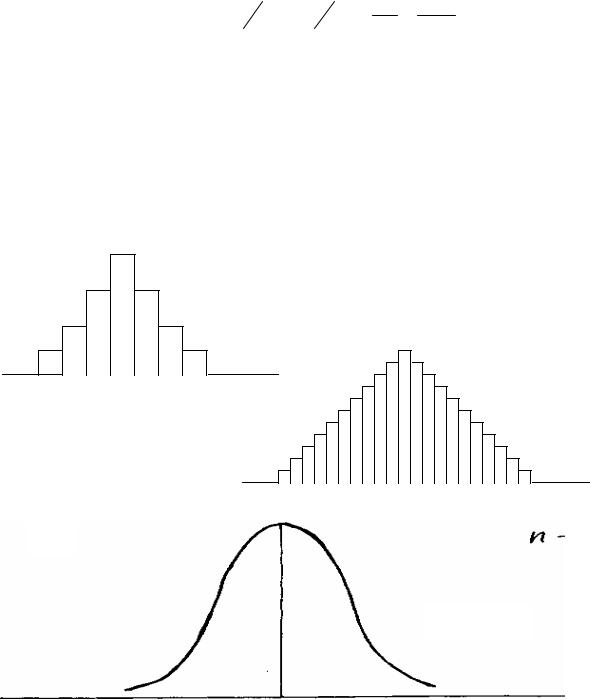
1 Частота у при любых значениях х будет положительной; это свидетельствует о том, что нормальная кривая расположена над осью абсцисс (рис. 5.3).
2 Поскольку х входит в уравнение во второй степени, результата замены положительных отклонений на отрицательные не изменится; следовательно, нормальная кривая симметрична относительно оси ОУ.
3 Кривая нормального распределения убывает по мере удаления от средней величины, а значит, большие отклонения появляются значительно реже, чем малые.

36
95,4%
99,7%
Рис. 5.3 Кривая нормального распределения
4 С увеличением отклонения х частота у быстро уменьшается, но значение нуля достигает только при х = ±∞; следовательно, ось абсцисс является асимптотой как для левой, так и правой ветви кривой.
5 Максимального значения у достигает при х = 0; таким образом, в точке, соответствующей среднему значению, ордината (частота) будет иметь наибольшую величину (рис. 5.3).
6 Кривая нормального распределения имеет точки перегиба. В то время как средняя часть имеет выпуклый характер, ветви кривой вогнуты. Точки перегиба
3
соответствуют отклонениям от центральной ординаты на ± 4σ .
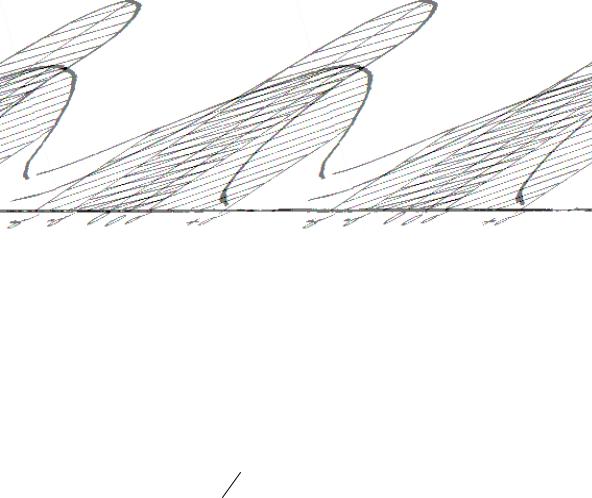
Вблизи точки перегиба кривая имеет наиболее крутой наклон. Очевидно, чем больше σ, тем шире размах кривой, а ее максимальная высота – ниже. И, наоборот, при малых σ размах кривой уже, а максимум высоты - выше. Значит, при малых σ кривая плотности нормального распределения «стягивается» к середине, а при больших σ она «расплывается» в стороны (рис. 5.4). При этом подразумевается, что в обоих случаях площади, ограничиваемые кривой и осью абсцисс, одинаковы.
7 Имеется определенное соотношение между основным отклонением и площадью нормальной кривой в пределах основного отклонения (рис. 5.4). В ту или другую сторону от среднего значения расположено около 68,3% всех единиц совокупности, в пределах удвоенного основного отклонения расположено около 95,4% и в пределах утроенного основного отклонения – около 99,7%. Таким образом, около 23 всех единиц совокупности, т.е. основная часть ряда распределения,
отклоняется от среднего значения не более чем на одно основное отклонение.
37
Весь ряд распределения исчерпывается в пределах ±3,5 σ.
А) |
|
В) |
|
|
|
|
|
|
Рис. 5.4 Кривая нормального распределения:
А) – характер кривой при «малой» величине основного отклонения; В) – характер кривой при «большой» величине основного отклонения
3 Вычисление теоретических частот по таблице площади и ординат нормальной кривой
Кривая нормального распределения имеет большое значение для вычисления теоретических частот. Для использования уравнения нормального распределения построены специальные таблицы, в одних из которых приведены значения
ординат функции: f (x) = eх2 2 , в других – значения площади нормальной кривой. Такие таблицы удобны для вычисления теоретических частот, для чего необходимо задать величины М, σ и N. Эти параметры полностью определяют форму и положение ряда распределения.
Вычислим частоты нормальной кривой для рассмотренного ранее вариационного ряда толщины деревьев.
Исходные данные: М = 31,4 см, σ = 6,9 см, N = 208. Используя подмеченную выше закономерность, – варианты колеблются около среднего значения в пределах ±3,5 σ, – найдем вероятные минимальную и максимальную варианты:
Vmin = M −3,5σ = 31,4 −3,5 6,9 = 7,25 см Vmax = M + 3,5σ = 31,4 + 3,5 6,9 = 55,55 см.
Установив размер ряда Pp =Vmax −Vmin = 55,55−7,25= 48,3см и приняв ту же величину интервала (4 см), перейдем к вычислению теоретических частот.

38
Схема вычисления частот по таблице ординат нормальной кривой приведена в таблице 5.3.
Вычисляют отклонения средних значений классов от среднего значения признака (графа 3), затем эти отклонения выражаются в долях сигмы (графа 4) и по ним из приложения 4 берутся значения f (x), представляющие собою частоты, выраженные в долях центральной ординаты. Чтобы найти теоретические частоты, нужно значения умножить на максимальную частоту, соответствующую среднему значению. Максимальную частоту находят по формуле
nmax = |
|
N |
|
. |
(5.13) |
|
|
|
|
|
|||
|
2π |
|||||
σ |
|
|
|
|
||
Эту формулу легко получить из общего уравнения нормальной кривой, если отклонение х принять равным нулю. Для рассматриваемого примера максимальная частота:
nmax |
= |
208 |
|
|
= 48,12. |
|||
|
|
|
|
|
||||
|
|
|
|
|
||||
1,725 |
6,28 |
|||||||
|
|
|
|
|||||
Таблица 5.3 Вычисление теоретических частот по таблице ординат
нормальной кривой
Среднее |
|
Откло- |
|
|
|
|
Значение |
|
Теоретические |
|||
значение |
Мср, см |
нения |
W − M |
|
|
функции, |
|
|
|
|
||
ср |
nmax |
частоты n |
||||||||||
классов |
|
α = W − M |
|
|
|
f (x) |
||||||
|
|
σ |
|
|
f (x)ּ n |
|||||||
|
|
|
|
|
||||||||
W, см |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
max |
||||
8 |
|
23,4 |
3,36 |
|
|
0,003 |
48,12 |
0,2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
12 |
|
19,4 |
2,81, |
|
0,019 |
48,12 |
0,9 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
16 |
|
15,4 |
2,23 |
|
|
0,083 |
48,12 |
4,0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
20 |
|
11,4 |
1,65 |
|
|
0,256 |
48,12 |
12,3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
24 |
|
7,4 |
1,07 |
|
|
0,564 |
48,12 |
27,2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
28 |
|
3,4 |
0,49 |
|
|
0,887 |
48,12 |
42,7 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
32 |
31,4 |
0,6 |
0,09 |
|
|
0,996 |
48,12 |
47,9 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
36 |
|
4,6 |
0,67 |
|
|
0,799 |
48,12 |
38,5 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
40 |
|
8,6 |
1,25 |
|
|
0,458 |
48,12 |
22,0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
44 |
|
12,6 |
1,83 |
|
|
0,187 |
48,12 |
9,0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
48 |
|
16,6 |
2,41 |
|
|
0,055 |
48,12 |
2,6 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
52 |
|
20,6 |
2,99 |
|
|
0,011 |
48,12 |
0,6 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
56 |
|
24,6 |
3,57 |
|
|
0,002 |
48,12 |
0,1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
ИТОГО |
|
|
|
|
|
|
|
|
208 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

39
Значение σ подставляют в формулу в условных единицах (в долях принятого интервала).
Для вычисления теоретических частот по таблице площади нормальной кривой расчет производится по следующей схеме (табл. 5.4).
Заполнение граф 1-5 пояснений не требует. Графа 6 заполняется по приложению 1. Например, отклонению 1,94 σ соответствует 47,4%. Эта цифра получается так: из таблицы берется значение 9476, соответствующее отклонению 1,94 σ; это соответствует 94,76% вариант, которые лежат по обе стороны от центра распределения, а значит, от среднего значения до отклонения 1,94 σ находится 94,76 : 2=47,4% вариант. Количество вариант в классе (графа 7) представляет собой разность между количеством вариант до высшего и низшего пределов класса. Например, количество вариант в классе 20 будет: 47,4-41,3=6,1%. Исключением является только тот класс, к которому относится средняя величина. В этом случае количество вариант до правого и левого пределов суммируется (7,9+14,8=22,7%).
Теоретические частоты, вычисленные по таблице площади и по таблице ординат нормальной кривой, близки между собой.
Рост и развитие деревьев и насаждений зависит от множества факторов. Различное их сочетание приводит к появлению случайных отклонений, что является характерным свойством изменчивых признаков.
Распределение таких случайных величин обычно получается при совместном воздействии ряда малых независимых (значит, случайно сочетающихся) факторов, число которых неограниченно велико.
Такое условие (одновременное воздействие большого числа малых по сравнению с общей суммой факторов) выполняется в природе довольно часто. Поэтому распределение Гаусса и принято называть нормальным. Однако, если какойлибо из факторов, не подчиняющийся сам нормальному распределению, играет преобладающую роль, то распределение не будет нормальным. Такие случаи не так уж редки. Поэтому нормальное распределение не следует считать универсальным.
Фактические ряды распределения показателей растительного мира часто значительно отклоняются от теоретических рядов. Приходится лишь говорить о том, в какой мере распределение данного признака приближается к нормальному.
