
Контактные сети и ЛЭП
.pdf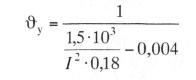
новившееся значение будет нарастать по гиперболе, например, для провода марки МФ-100 с = 0,39 Дж/(кг·К); при С = gγβ = 100·8,91·0,39 = 350 Вт·с/(° С·м); α = 0,004 1/° С, температура перегрева определяется:
и будет изменяться следующим образом:
I, А ……………………………………….200 |
400 |
800 1200 1400 |
|
ϑ , ºC..……………………………………. 5 |
25 |
118 530 |
∞ |
Кривая ϑt (t), построенная по уравнению (10.14), имеет экспоненциальный ха-
рактер (рис. 10.4). Определим на экспоненте длину подкасательной ВС, т. е. длину горизонтальной проекции касательной на участке кривой от точки касания до пере сечения с асимптотой ϑt = ϑу в точке С.
Рис. 10.3. Зависимость установившейся температуры от тока
При α>0
(10.21)
где АВ=ϑу -ϑt .
Используя выражения (10.14) и (10.18), будем иметь
(10.22)
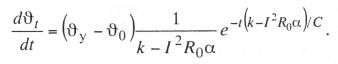
и
(10.23)
Подставив выражения (10.22) и (10.23) в уравнение (10.21), получим
(10.24)
т.е. длина по касательной ВС не зависит от момента времени t и остается постоян-
ной за все время роста температуры. Ее называют постоянной времени нагревания и обозначают τ
(10.25)
Рис. 10.4. Зависимость температуры от времени
Когда не учитывают влияние изменения температуры провода на его сопротив-
ление и принимают α = 0, постоянная времени будет выглядеть следующим обра-
зом:
(10.26)
Тогда выражение (10.15) с учетом уравнения (10.16) примет вид:
(10.27)
или
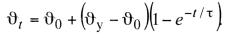
(10.28)
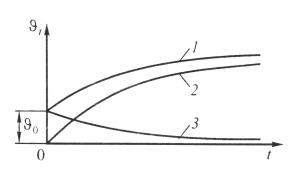
В выражении (10.27) значение ϑt , представлено двумя слагаемыми: первое сла-
гаемое представляет собой температуру провода в момент времени t при начальной температуре, равной 0 (рис. 10.5, кривая 2). Второе слагаемое учитывает начальную температуру ϑt , а кривая 3 – падение этой слагаемой во времени. Сумма этих кри-
вых и даст кривую 1 суммарной температуры ϑt . Подобно этому можно представить и процесс нагревания провода с учетом зависимости его сопротивления от темпера-
туры. Но здесь вопрос несколько сложнее. Первый член выражения (10.14) характе-
ризует рост температуры при отсчете от начальной температуры, равной нулю. Пока k > I2R0α, все протекает аналогично случаю, когда α = 0. Со вторым членом уравне-
ния (10.14) дело обстоит иначе. Как и в выражении (10.15), он здесь характеризует постепенное понижение слагающей начальной температуры ϑ0 . В то же время про вод обтекается током I и, следовательно, его сопротивление превышает сопротивле-
ние R0 не только за счет тока I, но и за счет слагающей от начальной температуры
ϑ0 . Поэтому понижение ϑt за счет составляющей от ϑ0 менее интенсивно. На рис. 10.6 кривые 6, 4 и 3 повторяют кривые, приведенные на рис. 10.5, а кривые 5,2 и 1
заменяют их соответственно при Rt> R0. Первый и второй члены выражения (10.14)
относятся к случаю, когда по проводу протекает ток I и α >0. Рассмотрим, что полу-
чится, если ток будет отключен и охлаждение начнется с температуры ϑ0 . Подста-
вим в выражение(10.14) I= 0:
(10.29)
Ток здесь не протекает и значение сопротивления не влияет ни на что. Если ток нагрузки в момент времени t0 резко уменьшился бы до нуля (рис. 10.7, а), то процесс охлаждения (кривая АВ на рис. 10.7, 6) будет описываться выражением (10.29), где вместо ϑ0 следует принять ϑ01 .
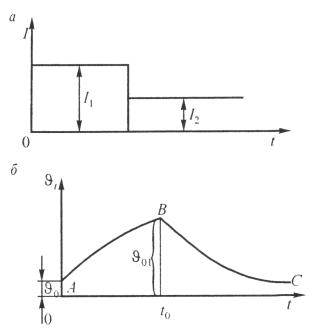
Если ток нагрузки изменяется от I1 до I2 (рис. 10.8, а), то при нагревании (кри-
вая АВ, рис. 10.8, 6) в выражении (10.14) ток I = I1 и устанавливается значение ϑ01 в
начале второго режима. Процесс охлаждения будет описываться также выражением
(10.14) (кривая ВС, рис. 10.8, б), но здесь ток будет равен I2.
Рис. 10.5. Кривые определения значений членов выражения для нагревания проводов
Рис. 10.6. Кривые определения значений членов формулы для нагревания провода при различных сопротивлениях
Рис. 10.7. Зависимость тока от времени (а) и кривая охлаждения провода при отключении тока (б)
Таким образом, если изменение тока в проводе представить ступенчатой лини-
ей (рис. 10.9), то на каждом участке кривая температуры будет строиться по выра-
жению (10.14) и через оба члена будет проходить один и тот же ток Ii, соответству-
ющий участку кривой тока. Здесь же будет определена начальная температура ϑ0i i-
го участка кривой тока. Температура ϑ0i будет зависеть от тока Ii-1 на i-1-м участке.
Кривая температуры на i-м участке будет зависеть от этой температуры и от тока на этом участке.
Рис. 10.8. Зависимость тока от времени (а) и кривая нагревания провода при уменьшении тока (б)
Рис. 10.9. Зависимость тока от времени (а) и кривая нагревания провода при изменяющемся токе (б)
Ранее были рассмотрены процессы нагревания проводов током, изменяющимся ступенчато. В действительности же ток в проводе контактной сети непрерывно из-
меняется. Поэтому при расчетах по выведенным формулам под током следует по-
нимать некоторое постоянное значение, эквивалентное по своему воздействию на старение провода.
Однако отсутствие математических зависимостей механических характеристик от температуры и времени ее действия не позволяет определить токи эквивалентно-
го значения. Поэтому приходится мириться с более грубыми допущениями. Далее под значениями токов будем понимать их эквивалентное значение по количеству выделяемого тепла (не по старению), т.е. так называемое «эффективное» значение
(среднее квадратичное), взятое за время, соответствующее поставленной задаче. Ес-
ли нагрузочные токи поездов в фидерной зоне не претерпевают резких и частых из-
менении, то под эквивалентным значением можно понимать их среднее значение за время хода по данной зоне.
10.3. Выбор расположения поперечных соединителей подвески
Как было приведено ранее, поперечные соединители предназначены для рас-
пределения тока контактной сети между отдельными ее проводами (несущий трос,
контактные, вспомогательные и усиливающие провода). Варианты их расположения представляют интерес с точки зрения нагревания проводов контактной сети, осо-
бенно на участках постоянного тока и в первую очередь контактного провода. При этом следует рассматривать такое расположение поездов, при котором ток в кон-
тактной сети достигает максимального значения.
Между смежными поездами одного направления всегда располагается несколь-
ко анкерных участков и, конечно, на одном и том же анкерном участке уж никак не может быть больше одного поезда.
Наибольшим в контактной сети будет ток на участке, примыкающем к под-
станции, и особенно в том случае, если все поезда в фидерной зоне размещены как можно ближе к этой подстанции. На рис. 10.10 первый поезд расположен около под-
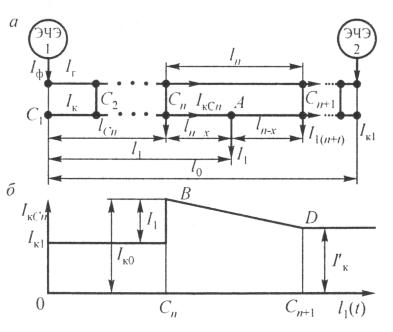
станции ЭЧЭ1, а следующий на минимально допустимом расстоянии от него. В
Рис. 10.10. Расчетная схема распределения тока в проводах
этом случае ток фидера Iф подстанции ЭЧЭ1, а следовательно, и ток в контактной сети Iк получают наибольшие значения. На схеме контактная сеть представлена двумя проводами с сопротивлениями rк и rт, Ом/км. Сопротивление rк относится к контактному проводу (одинарному или двойному), а сопротивление rт представляет собой эквивалентное сопротивление несущего троса и параллельно присоединенных к нему усиливающих проводов (эквивалентного провода). Контактный и эквива-
лентный провода на всем протяжении соединены поперечными соединениями С с
расстоянием ln, между ними, обычно равным 150—350 м, иногда и меньше. При па-
раллельной работе подстанций ток фидера подстанции (например, подстанции ЭЧЭI) определяют делением тока каждого поезда, находящегося в фидерной зоне,
на части, обратно пропорциональные их расстояниям от подстанции, и сложением соответствующих частей; при этом предполагается, что все провода контактной сети соединены параллельно. Это предположение соответствует и конечному числу по-
перечных соединений. На рис. 10.10, а показано расположение одного поезда в фи-
дерной зоне в точке А между поперечными соединениями Сn и Сn+1. Токи поездов принимают равными их средним значениям в фидерной зоне за время хода по зоне.
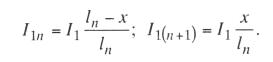
Ток фидера Iф и, следовательно, токи Iт и Iк слева от Сn зависят только от расстояния l1 (координаты нагрузки) и не зависят от координат (расположения) поперечных со-
единителей. Не нарушая токораспределения между подстанциями, ток I1 можно раз-
ложить на две составляющие между узловыми точками Сn и Сn+1 обратно пропорци-
онально расстояниям от этих составляющих до электровоза (точка А):
В свою очередь, токи I1n и I1(n+1) распределяются между подстанциями обратно пропорционально расстояниям до них. Следовательно, составляющая нагрузки фи-
дера подстанции ЭЧЭ1 Iф от тока I1 будет равна
Подставим значения I1n, I1(n+1) в это выражение и примем во внимание, что I1n + I1(n+1) = I1, тогда Iф = I1(l0 – l1)/l0. Полученный результат говорит о том, что распреде-
ление тока поезда между подстанциями не зависит от числа и расположения попе-
речных соединений.
При наличии двух поездов ток фидера подстанции ЭЧЭ1 Iф будет равен (ис-
пользуя метод суперпозиции)
(10.30)
где l2 — расстояние второго поезда от подстанции ЭЧЭ1.
Ток на участке от подстанции до Сn распределяется между проводами обратно пропорционально их сопротивлениям rк и rт.
Если принять, что сопротивление поперечного соединения равно нулю, то через все попёречные соединения, расположенные слева от Сn, ток не протекает, и поэто-
му их число и расположение не оказывают влияния на распределение тока между проводами. Во всех случаях ток протекает только через ближайшие к нагрузке по-
перечные соединения и не протекает через все остальные.
Наибольшая нагрузка ложится на контактный провод участка ln, на котором
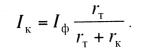
расположен электровоз. Следовательно, здесь и будет наиболее высокая температу-
ра провода.
В связи с этим следует подробнее рассмотреть нагрузку провода между теми поперечными соединениями, где расположен поезд. Ток в контактном проводе на участке между подстанцией и поперечным соединителем Сn
(10.31)
Ток в контактном проводе на участке Сn, А
(10.32)
Первое слагаемое определяется током, уходящим за пределы точки Cn+1, рав-
ным Iф—I 1. Согласно выражению (10.31)
(10.33)
Второе слагаемое Iк1, связано со значениями тока I1. Рассмотрим две параллель-
ные цепи, соединяющие точку Сn с точкой А: первая цепь с сопротивлением rкx и
вторая с сопротивлением rкln+rк(ln – x). Вторая составляющая тока в контактном проводе на участке СnА с учетом сопротивления обеих цепей будет равна
или после упрощения
(10.34)
Подставим в выражение (10.32) значения составляющих из формул (10.33) и (10.34). Тогда ток IкCn на участке СnА
(10.35)
При изменении х от 0 до ln изменяются составляющие всех нагрузок фидерной
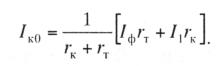
зоны и, в частности, составляющие тока I1 приходящиеся на подстанцию ЭЧЭ1. Так как ln во много раз меньше, чем l0, можно считать, что эти составляющие постоян-
ные. Тогда ток IкСn в контактном проводе на участке СnА представляется зависимо-
стью IкСn(l1) (рис. 10.10, 6).
В частном случае при l1 = lСn или иначе при х = 0
(10.36)
При х = ln, выражение (10.35) обращается в формулу (10.31) и ток на отрезке СnА (см. рис. 10.10, а) получает то же значение, что и на участке от ЭЧЭ1 до Сn. По-
ка ток I1, протекая от ЭЧЭ1 к ЭЧЭ2 располагается левее точки ln, справа от нее ток в проводе равен Iк1, что определяется по выражению (10.33). Как только поезд минует точку Сn, ток в контактном проводе увеличится скачкообразно и значение этого то-
ка, т.е. на I1 достигнет значения Iк0 и теперь уж будет определяться по выражению
(10.36). На отрезке СnA ток изменяется в зависимости от х, как это видно из выра-
жения (10.35), по закону прямой линии (см. рис. 10.10, б). Прямая ВD показывает,
как изменяется ток в контактном проводе на участке СnA при движении электровоза по участку ln, т.е. при изменении х от 0 до ln.
При постоянной скорости поезда расстояние х в соответствующем масштабе показывает время. В точке Сn эффективная нагрузка контактного провода будет наибольшей. Определим ее за время хода электровоза tn по участку СnСn+1. При рас-
положении поезда на расстоянии х от Сn [см. выражение (10.35)] ток Iк в этой точке будет:
За время хода электровоза по участку СnСn+1, т.е. за время tn, при постоянной скорости
(10.34)
