5 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА

Планирование эксперимента позволяет экспериментатору, пользуясь математическими методами, целенаправленно изменять условия опытов. Основываясь на имеющихся сведениях об изучаемом процессе, исследователь выбирает некоторую оптимальную методику для управления экспериментом. Процесс исследования обычно разбивается на отдельные этапы. После каждого этапа исследователь получает новую информацию, позволяющую ему изменять методику исследования.

Задача всего исследования формулируется следующим образом: нужно получить представление о функции отклика у=ϕ(х1, X2, ..., хm) (где у—параметр процесса, подлежащий оптимизации; x1, x2..... хm — независимые переменные — факторы, которые можно варьировать при постановке экспериментов).

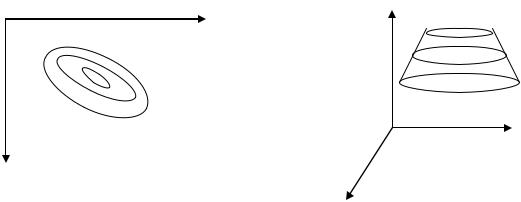
Координатное пространство с координатами х1, x2,…, хm называется факторным пространством, а геометрический образ, соответствующий функции отклика, называется поверхностью отклика, представленной на рисунке 6б.

Рисунок 6 – Поверхность отклика

При двух факторах поверхность отклика можно изобразить в виде проекций линий равного уровня на плоскость X1X2, представленной на рисунке 6а.

Задача планирования эксперимента формулируется так: на каждом этапе исследования нужно выбрать оптимальное расположение точек в факторном пространстве для того, чтобы получить некоторое представление о поверхности отклика. Оптимальность расположения точек определяется целью, к которой стремится экспериментатор на данном этапе.

Активный эксперимент можно назвать дважды оптимальным: он определяет

наилучшее соотношение независимых факторов для проведения технологического процесса, а методы проведения самого эксперимента оптимальны в том смысле, что позволяют решить задачу с минимальными затратами времени и средств. Тем не менее, существует другое название — экстремальные эксперименты, хотя экстремум далеко не всегда является оптимумом. Это название принято в статистике по традиции: к экстремальным задачам относят задачи отыскания максимумов и минимумов функции, если они являются оптимальными значениями.

Прежде чем заняться построением функции отклика, необходимо решить вопрос о том, сколько и какие факторы следует принять в рассмотрение, а также

29

провести так называемые отсеивающие эксперименты, цель которых — выделить доминирующие факторы среди большого числа возможных. После

определения доминирующих факторов необходимо приступить непосредственно к эксперименту.

5.1 Полный факторный эксперимент (ПФЭ). ПФЭ 23

Математическая модель технологического процесса, которую необходимо оптимизировать с помощью активного эксперимента; представляет собой уравнение регрессии. Чтобы получить независимые оценки - коэффициенты этого уравнения, нужно предъявить к фиксированным значениям независимых переменных некоторые требования. Таблица значений или уровней факторов при проведении каждого опыта (в дальнейшем будем называть ее матрицей планирования) должна иметь линейно независимые столбцы, а сумма произведений значений любых двух факторов, т. е. чисел двух столбцов, должна равняться нулю. Такую матрицу, называемую ортогональной, имеет полный факторный эксперимент.

Перед началом опытов на основании априорных данных выбирается технологический режим, который является базовым. Математическое описание объекта в окрестности точки базового режима хi0 может быть получено варьированием каждого из факторов Xi на двух уровнях, отличающихся от базового уровня на величину шага варьирования ± xi. Факторы должны быть независимые, т, е. допускать изменение любого из них на некоторую величину без изменения при этом всех других факторов.

Шаг варьирования по каждой переменной выбирается таким, чтобы

приращение величины выходного параметра Y к базовому значению при реализации шага можно было выделить на фоне «шума» при небольшом числе параллельных опытов. Шаг варьирования не должен быть ни слишком маленьким (не менее погрешности измерения фактора), ни слишком большим. Доля шага или

интервала варьирования для всей области возможных значений данного фактора выбирается в зависимости от конкретных условий каждого этапа эксперимента.

Полным факторным экспериментом (ПФЭ) можно считать эксперимент,

реализующий все возможные не повторяющиеся комбинации уровней независимых переменных, каждый из которых принудительно (активно) варьируется на двух уровнях. Число этих комбинаций при n факторах равно N=2n

иопределяет тип планирования.

Вдальнейшим рассмотрим планирование типа N=23, т. е. на примере

объекта с тремя факторами х1, x2, x3.

При планировании эксперимента проводят преобразование (нормализацию) независимых переменных xi; с помощью безразмерных переменных zi (Zi= (xi —

xi0)/ xi, что дает возможность легко построить ортогональную матрицу планирования и облегчает дальнейшие расчеты, так как верхний и нижний

уровни варьирования (ziверх когда хi0<хi, и ziнижн , когда хi0 >хi) равны соответственно + 1 и -1.

Для трехфакторной задачи нормализованное уравнение регрессии имеет вид

30

После введения фиктивной переменной z0=l, y=å(bizi).

Полный факторный эксперимент дает возможность найти раздельные оценки коэффициентов bi.

Нахождение модели методом полного факторного эксперимента состоит из планирования эксперимента, собственно эксперимента, проверки воспроизводимости (однородности выборочных дисперсий), получения

математической модели объекта с проверкой статистической значимости выборочных коэффициентов регрессии и проверки адекватности математического описания.

Построим матрицу планирования для трехфакторной задачи. При этом следует помнить, что полный факторный эксперимент — это весь возможный перебор неповторяющихся комбинаций уровней xi:

Матрицу удобно начать со строки (под строкой, как и в исходном журнале первичных данных, понимают условия и результат одного опыта), где все управляемые переменные находятся на нижнем уровне, т. е. z1=-1, Z2=-1, Z3=-1. Последующие строки (многомерные точки) выбираются по правилу: при

построчном переборе всех вариантов частота смены знака управляемых переменных для каждой последующей переменной вдвое меньше; чем для предыдущей. Поскольку все переменные могут принимать только значения +1 и —1, это позволяет в целях упрощения записывать в матрицу только знаки « + » и «-». Фиктивная переменная z0 во всех строчках имеет знак " + ". Количество строчек 2n = 23=8.

Таблица 9 - Матрица планирования трехфакторного эксперимента

Число строчек матрицы планирования, т. е. число опытов, возрастает по показательной функции 2n.

Построенный таким способом план эксперимента обладает рядом ценных свойств:

1.Симметричность относительно центра эксперимента: алгебраическая

сумма элементов столбцов для каждого фактора равна нулю åzji = 0 [где i - номер фактора (меняется от 1 до n); j - номер опыта (меняется от 1 до N).

2.Условие нормировки: сумма квадратов элементов каждого столбца равна

числу опытов åz2ij = N.

31

3. Сумма почленных произведений любых двух столбцов матрицы планирования равна нулю: åzijzky=0 i¹k, i, k=0, 1, 2, .... п.

Это важное свойство называется ортогональностью. Поэтому такие планы и их матрицы называют ортогональными.

Из последнего свойства следует взаимная независимость оценок коэффициентов уравнения регрессии.

При реализации полного факторного эксперимента, поскольку изменение выходной величины у носит случайный характер, приходится в каждой

многомерной точке проводить т параллельных опытов и результаты наблюдений

Весь эксперимент в этом случае делится на т серий опытов, в каждой из которых полностью реализуется матрица планирования.

Прежде чем строить математическую модель по результатам опытов, необходимо проверить, не было ли влияния на некоторые из них неучтенных факторов. Проверка воспроизводимости представляет собой проверку

выполнения предпосылки регрессионного анализа об однородности выборочных дисперсий S2yi

Задача состоит в проверке гипотезы о равенстве дисперсий S2y1 = S2y2 = S2y3=…= S2yn, при экспериментах во всех многомерных точках (8 точек для трех факторов). Оценки дисперсий находят по формуле

Если каждый опыт проводился трижды, та дисперсии получают по выборкам одинакового объема m=3, a число степеней свободы для всех дисперсий одинаково и равно т - 1=2.

Для проверки гипотезы об однородности оценок дисперсий следует пользоваться критерием Кохрена G, который основан на законе распределения отношения максимальной полученной дисперсии к сумме всех дисперсий. Расчетное значение критерия получают по формуле:

Для нахождения табличного значения критерия Кохрена рассчитывают f1=m-1; f2=N. Если вычисленное значение критерия Gp окажется меньше его табличного значения Gт, для выбранного уровня значимости (обычно α=0,05), то гипотеза об однородности дисперсий принимается. Это значит, что различий между дисперсиями не должно быть.

32

В этом случае можно рассчитать генеральную дисперсию

Имеющую f3==N(m— 1) степеней свободы.

Если проверка на воспроизводимость дала отрицательный результат, то

остается признать невоспроизводимость эксперимента относительно управляемых переменных вследствие флуктуации неуправляемых и неконтролируемых переменных, создающих на выходе большой уровень «шума». При этом следует повторить эксперимент с увеличенным числом параллельных опытов.

Построение математической модели объекта начинается с определения независимых оценок - коэффициентов bi по формуле:

bi = i=1 N

После этого необходимо проверить гипотезу о значимости коэффициентов bi, (проверка нуль-гипотезы bi=0).

Проверка гипотезы проводится с помощью t-критерия, который в данном

случае формируется как

где Sbi — среднеквадратическая ошибка, определения коэффициента bi при полном факторном эксперименте, равная

определенное по таблицам Стьюдента для числа степеней свободы f=N(m - 1) при заданном уровне значимости, т. е. sgn(tp — tкр) = «+», то гипотеза отвергается и коэффициент bi признается значимым.

В противном случае, если sgn(tp — tкр) =«–», нуль-гипотеза принимается и коэффициент bi - считают статистически не значимым (т. е. равным нулю).

Значимость коэффициентов можно оценить с помощью доверительного интервала:

Коэффициент полагается значимым, если выполняется неравенство: Abs(bj)>= bj

где abs(bj) – значения коэффициентов по модулю.

Статистическая незначимость коэффициента bi может быть обусловлена следующими причинами:

33

1)уровень базового режима xi0 близок к точке частного экстремума по переменной Xi (или по произведению переменных);

2)шаг варьирования xi- выбран малым;

3)данная переменная (произведение переменных) не имеет функциональной связи с выходным параметром y, т. e. bi = 0 по существу;

4)велика ошибка эксперимента вследствие флуктуации неуправляемых и неконтролируемых переменных.

Поскольку ортогональное планирование позволяет определять независимые оценки коэффициентов, то если какой-либо из коэффициентов окажется незначимым, он может быть отброшен без пересчета всех остальных.

После этого математическая модель объекта составляется в виде уравнения

связи выходного параметра у и переменных хi, включающего только значимые коэффициенты.

Чтобы, проверить гипотезу об адекватности результатов эксперимента найденным по уравнению связи, достаточно оценить отклонение предсказанной

уравнением регрессии выходной величины уiр от результатов эксперимента уi в точках факторного пространства.

Разброс результатов эксперимента относительно линии регрессий в этом

случае сравнивается с разбросом точек между собой. Первый разброс характеризуется дисперсией адекватности S2ад, оценка которой находится по

формуле

степеней свободы fад=N—n—1.

Второй (разброс точек) — дисперсией воспроизводимости S2воспр с числом степеней свободы fвоспр=N(m-1). Дисперсия воспроизводимости определяется по формуле (41).

Если S2ад < <S2воспр, то полученная математическая модель адекватно представляет результаты эксперимента.

Если S2ад >S2восп то нужно выяснить, случайно или не случайно различаются эти дисперсии, и если не случай но, то делается вывод о неадекватности уравнения.

Проверка гипотезы об адекватности проводится с использованием критерия

fвоспр=N(т— 1) при заданном уровне значимости а, то нуль-гипотеза принимается, т. е. уравнение адекватно при sgn(Fэксп—Fкр)="-". В противном случае гипотеза отвергается и описание признается неадекватным объекту.

Проверка адекватности возможна при fад>0.

34