
- •СОДЕРЖАНИЕ
- •ВВЕДЕНИЕ
- •1 ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ОПЫТНЫХ ДАННЫХ. ОТСЕВ ГРУБЫХ ПОГРЕШНОСТЕЙ
- •2 ПАССИВНЫЙ ЭКСПЕРИМЕНТ. КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ
- •2.1 Метод наименьших квадратов
- •2.2 Регрессионный анализ
- •2.3 Корреляционный анализ
- •2.4 Дисперсионный анализ
- •2.6 Реализация методов с помощью анализа данных в электронных таблицах Excel
- •2.7 Подбор уравнения регрессии при помощи линий тренда в электронных таблицах Excel
- •3 ПОИСКОВАЯ ОПТИМИЗАЦИЯ
- •3.1 Понятие линейного программирования
- •3.2 Типы задач, решаемые методами линейного программирования
- •3.2.1 Задача о наилучшем использовании ресурсов
- •3.2.2 Задача о выборе оптимальных технологий
- •3.2.3 Задача о смесях
- •3.3 Симплексный метод
- •3.4 Построение двойственных задач и их свойства
- •3.5 Реализация симплексного метода с помощью Поиска решения в электронных таблицах Excel
- •3.6 Алгоритм решения задачи о наилучшем использовании ресурсов
- •4 СТАТИСТИЧЕСКИЙ ДИСПЕРСИОННЫЙ АНАЛИЗ
- •4.1 Реализация дисперсионного анализа с помощью анализа данных в электронных таблицах Excel
- •4.2 Алгоритм реализации однофакторного дисперсионного анализа
- •5 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
- •5.1 Полный факторный эксперимент (ПФЭ). ПФЭ 2
- •5.2 Построение эксперимента в пакете Statgraphics Plus
- •5.3 Анализ математической модели и результатов эксперимента
- •5.4 Алгоритм реализации ПФЭ 2
- •6 СТАТИСТИЧЕСКИЕ ИГРЫ. КРИТЕРИИ ПРИНЯТИЯ РЕШЕНИЯ
- •7 ТРАНСПОРТНАЯ ЗАДАЧА
- •7.1 Постановка транспортной задачи по критерию стоимости
- •7.2 Построение начального опорного плана
- •7.3 Метод потенциалов
- •7.4 Условия оптимальности
- •7.5 Открытая модель транспортной задачи
- •8 Вопросы по дисциплине «Применение ЭВМ в отрасли»
- •Список литературы
- •Приложение А
- •Приложение Б
- •Приложение В
- •Приложение Г
- •Приложение Д
- •Приложение Е
Если гипотеза об адекватности отвергается, необходимо переходить к более сложной форме уравнения либо (если это возможно) проводить эксперимент с меньшим шагом варьирования хi.
Если математическая модель адекватна, то проверяют ее работоспособность. Проверка работоспособности осуществляется при помощи коэффициента детерминации. Расчет коэффициента детерминации может быть осуществлен по формуле (14). Если значение R2> 0,7 то математическая модель является работоспособной. В противном случае математическую модель нельзя использовать для прогнозирования результатов, т.к. она не является работоспособной.
5.2 Построение эксперимента в пакете Statgraphics Plus
Для построения эксперимента выполняются следующие действия:
1.Открывается пакет STATGRAPHICS PLUS.
2.Выбирается меню Special, подменю Experimental Design, команду
Create Design.
3.В открывшемся диалоговом окне в области Design Class устанавливается маркер напротив команды Screening. В строке No. of Response Variables устанавливается 1. В строке No. of Experimental Factors
устанавливается 3. Нажимается кнопка Ok.
4.Для каждого из трех факторов выставляются значения нижнего (-1,0)
иверхнего (1,0) уровней. Даются названия каждому фактору.
5.В следующем диалоговом окне в строке Name дается имя выходного показателя, на который оказывают влияние факторы, указанные в предыдущем окне.
6.В следующем диалоговом окне выбирается, какой эксперимент необходимо провести (ПФЭ 23).
7.В следующем диалоговом окне убирается галочка напротив команды
Randomize.
8.После чего открываем расчетную таблицу, в которую вносятся средние значения выходного показателя Y.
9.Сохраняем документ.
10.В окне Screening Design Attributes выбирается на панели инструментов кнопка Tabular Options.
11.В открывшемся диалоговом окне нажимается кнопка All.
12.Выбирается меню Special, подменю Experimental Design команда
Analyze Design.
13.В диалоговом окне Analyze Design выбирается параметр Y.
14.В окне Analyze Experimental на панели инструментов выбирается кнопка Graphical Options. В открывшемся диалоговом окне нажимается кнопка
All. В результате в окне программы отобразятся все расчеты и графические зависимости.
35
5.3 Анализ математической модели и результатов эксперимента
Коэффициенты при независимых переменных указывают на силу влияния факторов: чем больше численная величина коэффициента, тем большее влияние оказывает фактор. Если коэффициент имеет знак « + », то с увеличением значения фактора параметр оптимизации у увеличивается, а если «-» - уменьшается.
Величина коэффициента соответствует вкладу данного фактора в величину параметра оптимизации при переходе фактора с нулевого уровня на верхний или на нижний.
Иногда удобно оценивать вклад фактора при переходе от нижнего уровня к верхнему (либо наоборот), а не к нулевому. Вклад, определенный таким образом, называется эффектом фактора (иногда его называют основным или главным эффектом). Он численно равен удвоенному коэффициенту. Для качественных факторов, варьируемых на двух уровнях, основной (нулевой) уровень зачастую не имеет физического смысла. Поэтому понятие «эффект фактора» является здесь естественным.
Известно, что большинство тепло-, массообменных и других технологических процессов пищевой .промышленности подчиняются степенной (у = хтan) или экспоненциальной (у=a exp x) закономерности.
Вместе с тем никаких затруднений в описаний этих закономерностей уравнениями в виде полиномов и физической интерпретации результатов нет. Известно, что «выравнивание», или линеаризация степенного уравнения, производится логарифмированием его обеих, частей, а экспоненциального уравнения - только правой его части. После этого факторы заменяют логарифмами и производят все расчеты как для обычного уравнения регрессии. Отклик в первом случае также заменяется его логарифмом. Выравнивать можно и большинство других закономерностей.
Таким образом, возможности физической интерпретации уравнений в полиномах шире, чем других, поскольку они позволяют учесть взаимное влияние, или эффекты взаимодействия факторов.
Более полной формой анализа результатов является геометрическая интерпретация результатов ПФЭ.
Известно, что графически можно показать только непрерывную связь между двумя переменными. Зависимости функции от других аргументов можно изобразить дискретно, т. е. параметрически, или непрерывно, но в искаженном виде с помощью аксонометрических построений. При интерпретации результатов ПФЭ используются оба эти метода, но предпочтение отдается первому вследствие его простоты.
Например, изучалось влияние гидротермической обработки риса-зерна на пищевую (биологическую) ценность рисовой каши. Обработка состояла в пропаривании зерна, поэтому в качестве факторов были приняты время пропаривания x1, и давление пара x2. За функцию отклика у принята атакуемость белков каши, сваренной из обработанного зерна, одним из пищеварительных ферментов - пепсином.
36
Уравнение регрессии, полученное в результате ПФЭ, является неполным квадратный уравнением: у= 179.75 – 18.25z1 – 8,75z2 – 25,75z1z2. Это уравнение также удовлетворило всем требованиям статистического анализа (проверка значимости коэффициентов с помощью (t-критерия, проверка адекватности уравнения по F-критерию).
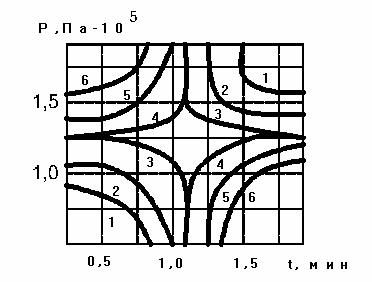
Геометрическая интерпретация представлена на рисунке 7. По.
координатным осям отложены в размерном выражении время обработки t и давление пара P. Значении функции отклика .(в миллиграммах пептина на 1 г в час) отложены в виде семейства кривых: 1 - 160; 2 - 180; 3-185; 4 - 187; 5 - 190; 6 - 200.
Эти кривые имеют вид равнобочных гипербол с асимптотами, которые совпадают по направлению с координатными осями. Геометрический анализ кривых показывает, что между значениями функции отклика 185 и 187 они должны выродиться в точку. Эта особая точка называется минимаксом. В ней пересекаются асимптоты, делящие координатное поле на квадранты с разными свойствами (в I и III при удалении от минимакса функция отклика уменьшается, во II и IV – растет).
Выбор II или IV квадранта для оптимизации процесса гидротермической
обработки в данном случае должен быть определен из условий оптимальности другого (дополнительного) критерия - товарного (кулинарного) качества рисовой крупы. Поскольку с увеличением t и уменьшением р (IV квадрант) не происходит ухудшения цвета крупы, который является основным показателем. товарного качества, оптимум следует искать именно в этом квадранте.
Рисунок 7 – Параметрическая диаграмма
Второй способ анализа результатов с помощью аксонометрических построений позволяет определить оптимальную область проведения эксперимента с помощью максимума или минимума на поверхности отклика или на проекции линий равного уровня, рисунок 6.
Значимость коэффициентов модели определяют также при помощи карты Парето. Карта позволяет оценить значимость коэффициентов, а соответственно и степень влияния факторов на выходной параметр Y. Карта Парето представляет собой гистограмму, пример представлен на рисунке 8.
37
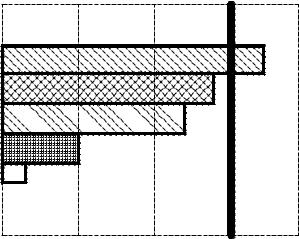
Рисунок 8 – Карта Парето
5.4 Алгоритм реализации ПФЭ 23
1.В соответствии с заданием из приложения 4 строится матрица планирования.
2.Производится усреднение значений выходного параметра Y по формуле
(38).
3.Находятся оценки дисперсий по формуле (39).
4.Определяется расчетное значение критерия Кохрена по формуле (40). Делается вывод об однородности дисперсий.
5.Определяется дисперсия воспроизводимости по формуле (40).
6.Определяются коэффициенты математической модели (41).
7.Определяется значимость коэффициентов математической модели при помощи формулы (45).
8.Составляется математическая модель с учетом только значимых коэффициентов.
9.Определяется среднеквадратическая ошибка Sbi (44).
10.Рассчитывается дисперсия адекватности Sад (46).
11.Определяется критерий Фишера (47). Делается вывод об адекватности математической модели.
12.Определяется работоспособность адекватной модели (14).
13.Осуществляется построение ПФЭ 23 в пакете Statgraphics Plus.
14.Производится анализ математической модели и результатов эксперимента.
Задания по данной теме находятся в приложении Г.
38
