Например, оптимальный опорный план задачи о наилучшем использовании ресурсов представлен в таблице 5.
Таблица 5 – Оптимальный опорный план
БП |
|
СБ |
А |
X1 |
X2 |
X3 |
X4 |
X5 |
|
X6 |
X7 |
|
30 |
140 |
160 |
20 |
|
0 |
0 |
0 |
|||
x5 |
|
0 |
56,667 |
0 |
0,0136667 |
0 |
0,003 |
|
1 |
-0,66667 |
0 |
x3 |
|
160 |
9166,7 |
1,25 |
1,1666667 |
1 |
0,5 |
|
0 |
83,33333 |
0 |
x2 |
|
0 |
45 |
-0,0015 |
0,003 |
0 |
0,009 |
|
0 |
-0,5 |
1 |
|
ЦФJ-CJ |
1E+06 |
170 |
46,666667 |
0 |
60 |
|
0 |
13333,33 |
0 |
|
При анализе оптимального опорного плана устанавливается соответствие между прямыми переменными и переменными двойственной задачи, в данном примере соответствие будет выглядеть следующим образом:
БП |
|
СБ |
|
||
x5 |
x6 x7 |
x1 |
x2 |
x3 |
x4 |
c |
c c |
c |
c |
c |
c |
y1 |
y2 y3 |
y4 |
y5 |
y6 |
y7 |
Оптимальный план двойственной задачи следующий: Y*= (0; 13333,33; 0; 170; 46,7; 0; 60)
Анализируя оптимальный план двойственной задачи получается, что y2*>0 – ресурсы второго вида используются полностью. Y1*=0 и y3*=0 ресурсы первого и третьего вида используются полностью. Y4*=170, y7*=60 при выпуске продукции первого и четвертого вида, не вошедшей в оптимальный план уровень прибыли будет снижаться на данные величины y4* и y7*.
3.5 Реализация симплексного метода с помощью Поиска решения в электронных таблицах Excel
Данный способ решения наиболее удобный и быстрый. Для реализации
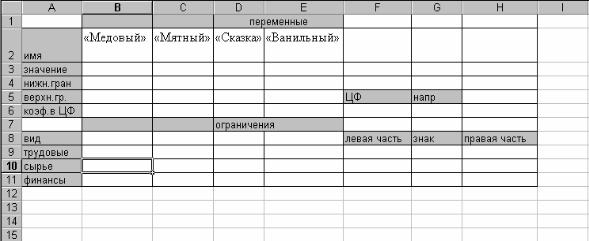
симплексного метода с помощью Поиска решения в электронных таблицах Excel необходимо создать электронную форму, которая является шаблоном для решения задачи о наилучшем использовании ресурсов. Вид формы представлен на рисунке 4.
Рисунок 4 - Форма для расчета с помощью Поиска решения
22
Встроку «Коэффициенты в целевую функцию» вводятся данные строки Прибыль из варианта задания (Приложение Б).
В«Ограничения» вносится расход соответствующего ресурса на единицу продукции.
Встолбец «Правая часть» заносятся значения столбца «Наличие» из варианта задания.
Вячейку ЦФ F6 вводится зависимость для целевой функции.
1). Вызывается Мастер функций. Выбирается категория Математические, функция СУММПРОИЗВ.
2). В открывшемся диалоговом окне в строке массив 1 вводится диапазон
B3:E3, рисунок 4.
3). В строку массив 2 вводится диапазон B6:E6.
4). Нажимается кнопка Готово.
В ячейки F9, F10, F11, которые рассчитывают расход каждого ресурса при выпуске всех видов продукции, вводятся зависимости для левых частей ограничений. Для этого:
1)копируется содержимое ячейки F6 (ЦФ) в ячейку F9, F10, F11;
2)В ячейке F9 редактируется формула и принимает следующий вид: =
СУММПРОИЗВ(B$3:E$3;B9:E9);
3)В ячейке F10 редактируется формула и принимает следующий вид: =
СУММПРОИЗВ(B$3:E$3;B10:E10);
4)В ячейке F11 редактируется формула и принимает следующий вид: =
СУММПРОИЗВ(B$3:E$3;B11:E11);
На этом ввод данных в форму закончен.
1.Выбрать меню Сервис, команду Поиск решения.
2.На экране отобразиться окно Поиск решения (рисунок 5). В строке «Установить Целевую ячейку» указывается ячейка $F$6 – ячейка ЦФ. Установить маркер напротив Равной Максимальному значению.
3.В поле Изменяя ячейки указать диапазон $B$3:$E$3.
4.В поле Ограничения вводятся ограничения для расчета Целевой функции. Для этого нажимается кнопка Добавить и в появившемся окне вводятся следующие ограничения: $B$3>=$B$4; $C$3>=$C$4; $D$3>=$D$4; $E$3>=$E$4; $F$9<=$H$9; $F$10<=$H$10; $F$11<=$H$11. После ввода последнего ограничения вместо кнопки Добавить нажимается кнопка ОК.
5.На экране появится диалоговое окно с введенными условиями.
6.Нажимается кнопка Параметры.
7.В появившемся диалоговом окне вводятся параметры поиска решения, а именно в поле Максимальное время вводится 100 секунд; предельное число итераций – 100, относительная погрешность – 0,000001; допустимое отклонение 5
%.Устанавливается галочка напротив команды Линейная модель. В поле Оценка устанавливается маркер напротив команды Линейная. В поле Производные устанавливается маркер напротив команды Прямые. В поле Метод устанавливается маркер напротив команды Ньютона. Нажимается кнопка ОК.
23