
- •1.4. Макроскопические модели электромеханических систем
- •1.4.1. Основные понятия и определения
- •1.4.2. Модель электрической подсистемы
- •1.4.3. Модель магнитной подсистемы
- •1.4.4. Модели механической подсистемы
- •1.4.5. Модель тепловой подсистемы
- •1.4.6. Топологические уравнения. Построение эквивалентных схем
- •1.6. Механические узлы электрических аппаратов
- •1.6.1. Механизмы электрических аппаратов
- •1.6.2. Блок щелчковых контактов
- •1.6.3. Механизм свободного расцепления
- •1.6.4. Механический узел контактора постоянного тока
- •1.6.5. Механический узел контактной системы реле с замыкающимися контактами
- •1.6.6. Механический узел контактной системы реле с размыкающимися контактами
- •1.7. Электромагнитные и магнитоэлектрические системы
- •1.7.1. Электромагнитный дроссель в фильтре выпрямителя
- •1.7.2. Электромеханические преобразователи электромагнитного типа
1.6.4. Механический узел контактора постоянного тока
Анализ работы электромеханической системы электрического аппарата включает расчет статических характеристик и динамики его работы вместе с механическими узлами. Для этого требуется построение математической модели механического узла аппарата, которая базируется на методах макромоделирования, приведенных в разделе 1.4.1.
У контактора постоянного тока, изображенного на рис. 1.44, механический узел составляют якорь 1, на который действует момент электромагнита. Якорь вращается на опоре. При выключенном электромагните якорь возвращается в исходное положение возвратной пружиной3. На якоре жестко закреплен узел подвижного контакта6, состоящего из основания4с опорой7и поджимной пружины контакта5. Электромагнит закреплен на неподвижном основании, где установлен также неподвижный контакт8. Для построения модели механического узла будем рассматривать только один полюс контактной системы. Другие полюса – аналогичные.

Рис. 1.44. Механический узел контактора постоянного тока (см. рис. 1.18).
Якорь и узел подвижного контакта совершает вращательное движение. Подвижный контакт внутри своего узла и возвратная пружина якоря двигаются поступательно. При малых перемещениях движение подвижного контакта относительно неподвижного можно рассматривать как поступательное. Все движения происходят в одной плоскости (планарная система).
Сначала построим граф кинематической схемы узла (см. рис. 1.45). Обозначим вершинами графа элементы, где требуется определить скорость движения: А- якорь,Бподвижный контакт. Неподвижное основание обозначимО. Ребрами графа будут элементы узла. Зазоры между якорем и электромагнитом, подвижным контактом и опорой и между контактами должны быть представлены моделями упоров (пружины с трением).

Рис. 1.45. Граф механического узла контактора рис. 1.44.
Якорь соединен с неподвижным основанием электромагнитным моментом Мэм, упором между якорем и электромагнитомУп1-2, трением в опоре вращения Тр3, моментом инерции якоря с узлом крепления подвижного контактаJ2и возвратной пружинойПр4.Подвижный контакт соединен с неподвижным основанием своей массой m7 и упором между контактамиУп7-9. Между якорем и подвижным контактом подключены элементы: поджимная пружинаПр6,трение в опоре скольжения контактаТр7и упор между подвижным контактом и опоройУп7-8. Якорь (вершинаАв графе) совершает вращательное движение, а подсоединенные к якорю элементыПр4,Пр6,Тр7иУп7-8 двигаются поступательно в своих системах координат:Пр4в неподвижной, аПр6, Тр7 иУп7-8 вращаются вместе с якорем. Поэтому для согласования элементов модели необходимо использовать преобразование вращательного движения в поступательное.
По построенному графу рис. 1.45 составляется эквивалентная схема. В принятых в Matlab Simulink (Simscape Mechanical) [26] мнемонических обозначениях элементов эта схема имеет вид, показанный на рис. 1.46. В ней использованы те же наименования элементов, что и на графе механизма, а также два согласующих преобразователя вращательного движения в поступательное. ЭлементV Пр1преобразует угловую скорость якоря в линейную скорость возвратной пружины в точке присоединения к якорю, т. е. умножает угловую скорость на плечо от опоры вращения якоря3до точки присоединения возвратной пружины. ЭлементV Пр6делает аналогичное преобразование вращательного движения в поступательное с плечом от опоры вращения якоря до точки присоединения поджимной пружины подвижного контакта.

Рис. 1.46. Эквивалентная схема механического узла контактора рис.1.42 в мнемонических обозначениях в Matlab Simulink (Simscape Mechanical).
Для построения
статической механической характеристики
контактора - зависимости момента нагрузки
на якорь от угла поворота якоря в схеме
рис. 1.46 исключаются инерционные элементы:
момент инерции J2якоря и масса подвижного контактаm7.
Действующий на якорь электромагнитный
момент задается линейно нарастающей
функцией (см. рис. 1.47). В качестве примера
на рис. 1.46 показаны результаты расчета
механической характеристики для
следующих параметров контактной системы:
поворот якоря ограничиваетУп1-2в
диапазоне углов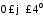 с начальным углом
с начальным углом ;
ход подвижного контакта до опоры
ограничиваетУп7-8в диапазоне
перемещений
;
ход подвижного контакта до опоры
ограничиваетУп7-8в диапазоне
перемещений ;
расстояние между подвижным и неподвижным
контактомУп7-9изменяется в пределах
;
расстояние между подвижным и неподвижным
контактомУп7-9изменяется в пределах ;
трение в опоре вращения якоряТр3только вязкое сkтр=0.5e-3
Нмс/рад; трение в опоре скольжения
подвижного контактаТр7также только
вязкоеkтр=1.0e-2 Нс/м; возвратная
пружинаПр1 имеет жесткостьkу1=1200
Н/м и начальное поджатие
;
трение в опоре вращения якоряТр3только вязкое сkтр=0.5e-3
Нмс/рад; трение в опоре скольжения
подвижного контактаТр7также только
вязкоеkтр=1.0e-2 Нс/м; возвратная
пружинаПр1 имеет жесткостьkу1=1200
Н/м и начальное поджатие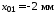 ;
поджимная пружина подвижного контактаПр6имеет жесткостьkу6=5000
Н/м и начальное поджатие
;
поджимная пружина подвижного контактаПр6имеет жесткостьkу6=5000
Н/м и начальное поджатие .
Электромагнитный момент задан функцией
.
Электромагнитный момент задан функцией .
.

Рис. 1.47. Модель механизма контактора для расчета механической характеристики.
Результаты расчета
механической характеристики представлены
на рис. 1.48. По оси Y указаны значения
момента нагрузки в Ньютонах, а по оси X
угол поворота якоря в радианах. В
начальный момент угол якоря равен нулю
и не изменяется до значения момента,
созданного предварительно поджатой
пружиной Пр1,т.е.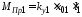 ,
где
,
где - плечо от точки закрепления пружины до
опоры вращения якоря. Далее момент
практически линейно возрастает при
малых изменении угла
- плечо от точки закрепления пружины до
опоры вращения якоря. Далее момент
практически линейно возрастает при
малых изменении угла в соответствии с заданной линейной
жесткостью возвратной пружины, приведенной
к моменту якоря
в соответствии с заданной линейной
жесткостью возвратной пружины, приведенной
к моменту якоря .
При касании подвижного и неподвижного
контактов, когда угол
.
При касании подвижного и неподвижного
контактов, когда угол ,
где
,
где – начальный зазор между контактами (2
мм, см.Уп7-9);
– начальный зазор между контактами (2
мм, см.Уп7-9); – плечо якоря до точки присоединения
пружиныПр6, угол остается неизменным
до значения момента, увеличенному на
добавленный момент силы предварительно
поджатой пружины контактаПр6, т.е.
– плечо якоря до точки присоединения
пружиныПр6, угол остается неизменным
до значения момента, увеличенному на
добавленный момент силы предварительно
поджатой пружины контактаПр6, т.е.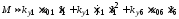 .
После этого момент линейно возрастает
с углом наклона линии, определенным
суммарной жесткостью возвратной пружины
якоря и поджимной пружины контакта со
своими плечами:
.
После этого момент линейно возрастает
с углом наклона линии, определенным
суммарной жесткостью возвратной пружины
якоря и поджимной пружины контакта со
своими плечами: .
.
При достижении
упора якоря Уп1-2 дальнейшее движение
прекращается. Это угол или 0.07 рад.
или 0.07 рад.

Рис. 1.48. Механическая характеристика контактора.
Анализ динамики работы механического узла удобно выполнить при импульсном характере электромагнитного момента по схеме рис. 1.49. Для рассматриваемого примера импульс момента и зависимости от времени угла поворота якоря и перемещения подвижного контакта приведены на рис. 1.50.

Рис. 1.49. Модель механического узла для анализа динамики работы в импульсном режиме.

Рис. 1.50. Зависимости момента электромагнита, угла поворота якоря и перемещения подвижного контакта от времени.
