
- •1.4. Макроскопические модели электромеханических систем
- •1.4.1. Основные понятия и определения
- •1.4.2. Модель электрической подсистемы
- •1.4.3. Модель магнитной подсистемы
- •1.4.4. Модели механической подсистемы
- •1.4.5. Модель тепловой подсистемы
- •1.4.6. Топологические уравнения. Построение эквивалентных схем
- •1.6. Механические узлы электрических аппаратов
- •1.6.1. Механизмы электрических аппаратов
- •1.6.2. Блок щелчковых контактов
- •1.6.3. Механизм свободного расцепления
- •1.6.4. Механический узел контактора постоянного тока
- •1.6.5. Механический узел контактной системы реле с замыкающимися контактами
- •1.6.6. Механический узел контактной системы реле с размыкающимися контактами
- •1.7. Электромагнитные и магнитоэлектрические системы
- •1.7.1. Электромагнитный дроссель в фильтре выпрямителя
- •1.7.2. Электромеханические преобразователи электромагнитного типа
1.4. Макроскопические модели электромеханических систем
1.4.1. Основные понятия и определения
Электромеханические системы электрических аппаратов [4] – сложные для моделирования объекты. Они отличаются разнообразностью конструкций и происходящих в них физических процессов. Подробная математическая модель устройств имеет большое число неизвестных параметров и требует значительных вычислительных ресурсов при анализе. Электромеханическая система в широком смысле включает помимо основных частей всё, что связывает ее с внешней средой и с источниками энергии, саму внешнюю среду и источники энергии.

Рис. 1.18. Контактор постоянного тока серии КПВ-600: 1 — дугогасящая катушка; 2, 15 — скобы; 3 — пластина магнитного дутья; 4 — неподвижный контакт; 5 — дуга; 6 — подвижный контакт; 7 — опора; 8 — контакт- рог; 9, 10, 12 — пружины; 11 — обмотка; 13, 16 — выводы; 14 — гибкий проводник; 17 — основание
При моделировании процессов описание электромеханической системы электрического аппарата, например контактора на рис. 1.18, разделяют на части или подсистемы с одним видом преобразуемой энергии. Электрическая подсистемапредставляет передачу энергии электрического тока от источника питания к катушке электромагнита и включает детали: источник питания, провода и катушку. Вмагнитной подсистемеосуществляется распределение энергии электромагнитного поля, существующего в деталях электромагнита: катушке, намагничиваемых магнитопроводе и других деталях из магнитных материалов, а также в окружающем пространстве. Вмеханической подсистеме(на рис. 1.18 выделена красным цветом) происходит преобразование механической энергии движения деталей механизма контактора под действием электромагнитных сил, сил упругости пружин, трения и инерционных сил.Тепловая подсистемапредставляет распространение тепловой энергии в деталях контактора и в окружающем пространстве.
Модели подсистем описывают процессы преобразования энергии только своей физической природы. Модель отдельной подсистемы должна устанавливать правила преобразования энергии своего вида, а также связывать различные подсистемы.
Физический процесс происходит в пространстве и во времени. Даже в ограниченном диапазоне пространственно-временных координат имеем бесконечное множество значений параметров, характеризующих процесс. Для построения математических моделей конечной размерности применяются аппроксимирующие функции, которые позволяют приближенно определить значения параметров в любой точке пространства и в любой момент времени по значениям в ограниченном числе узловых точек пространства и моментов времени. Чем больше узловых точек, тем точнее производится аппроксимация. Поэтому такие модели имеют асимптотическое уточнение решения. В зависимости от точности пространственной аппроксимации параметров принято разделять микромоделиимакромодели.
Микромодельимеет множество узлов для аппроксимации в пространстве, в общем случае изменяющихся во времени функций, которые выбираются с учетом характера пространственно-временного распределения параметров. Так решаются задачи численного анализа векторных или скалярных полей, например расчет поля вектора магнитной индукции электромагнита. Сама модель — это системы уравнений: дифференциальных в частных производных, интегродифференциальных или интегральных для функций координат и времени. При численном решении все типы уравнений сводятся к алгебраическим для последующего решения на компьютере.
Макромодельнаоборот использует грубую пространственную аппроксимацию параметров, которая позволяет не учитывать зависимости параметров процессов от пространственных координат. Она удобна там, где имеются сосредоточенные в пространстве элементы моделирования, например в электрической цепи – резистор, конденсатор или катушка индуктивности. В механике твердые тела представляются системой материальных точек со своими массами и воздействующими на них сторонними силами, силами трения и силами упругих связей с другими материальными точками. Математическая макромодель физической системы – это замкнутая система алгебраических и обыкновенных дифференциальных (интегральных) уравнений с одной независимой переменной – временем.
Макромодель составляется из элементов, не имеющих пространственных размеров. Свойства отдельных деталей моделируемого объекта представляются в ней интегральными параметрами, выраженными в виде констант или простых алгебраических функций. Определение параметров моделей отдельных элементов выделяется в самостоятельную задачу.
Составление математической модели системы, включающей несколько подсистем различной физической природы, основано на общих для всех подсистем понятиях, позволяющих добиться единообразия формы записи уравнений. К ним относятся [12] понятия фазовых переменных и элементов. Физические процессы представляются в виде зависимостей от времени определенных параметров, которые составляют совокупность искомых неизвестных математической модели и носят название фазовых переменных. По своему характеру такие переменные в каждой подсистеме могут быть отнесены к одному из двух типов: переменные типапотокаи переменные типапотенциала, например токiи напряжениеUв электрической цепи. Фазовые переменные обычно выбираются из условия, что их произведения определяют мощность преобразуемой энергии, а тип (поток или потенциал) с точки зрения математического моделирования может быть назначен произвольно. Кроме того, фазовые переменные должны быть удобны для записей физических законов в традиционной форме.
Названия пассивных элементов макромодели для любой из подсистем одинаковы и связаны с характером преобразования энергии в них. Таких элементов три. По аналогии с электрическими цепями их обозначают и называют: резистор, катушка индуктивности и конденсатор, добавляя общее слово: электрический, магнитный, механический, тепловой и т.п.
В резисторе
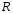 происходит безвозвратное рассеяние
энергии
происходит безвозвратное рассеяние
энергии .
В катушке индуктивности
.
В катушке индуктивности и конденсаторе
и конденсаторе
 ,
накапливается энергия
,
накапливается энергия ,
гдеU, i
—параметры процесса (для каждой
подсистемы свои);
,
гдеU, i
—параметры процесса (для каждой
подсистемы свои); — время.
— время.
Источники энергии в физических подсистемах моделируются источниками фазовых переменныхдвух типов: источники типа потока (аналог источника тока в электрических цепях) и источники типа потенциала (источник ЭДС в электрических цепях). В графическом представлении математическая модель изображаетсяэквивалентными схемамиподобно электрическим цепям, содержащим требуемый набор активных и пассивных элементов.
Составляющие математическую модель уравнения определяют связи между фазовыми переменными. По смысловому содержанию формируемые уравнения объединяются названиями либо компонентных, либо топологических уравнений.
Компонентные уравненияотражают закон функционирования каждого элемента системы и связывают разнородные фазовые переменные (поток — потенциал). Они выводятся как на основе известных фундаментальных законов и их следствий (например, второй закон Ньютона в механике), так и на основе данных специальных теоретических или экспериментальных исследований (в частности, микромоделированием полей, физическим макетированием и др.).
Топологические уравненияотражают структуру связей между различными элементами в подсистеме и в целом в системе и записываются для однородных фазовых переменных: отдельно для потоков и потенциалов. Вывод топологических уравнений легко поддается формализации, так как опирается на общие правила функционирования любых технических подсистем, представляющие законы непрерывности и равновесия.
Благодаря существующему подобию процессов различной физической природы по отношению к накоплению и рассеянию энергии конкретного вида, компонентные уравнения различных подсистем имеют одинаковые записи. Подобие процессов выражается в пропорциональном изменении во времени фазовых переменных. Поэтому модели различных подсистем можно представить совокупностью моделей одной подсистемы, например привычной для нас электрической цепью.
Для выявления возможного подобия процессов должны быть выполнены два требования к математической записи уравнений [12].
Уравнение физического процесса представляет сумму однородных слагаемых
 ,
гдеn — число
слагаемых уравнения,
,
гдеn — число
слагаемых уравнения,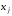 — параметры слагаемого. Это значит,
что все слагаемые имеют одну и ту же
размерность (правило Фурье).
— параметры слагаемого. Это значит,
что все слагаемые имеют одну и ту же
размерность (правило Фурье).Уравнение физического процесса должно быть полным, т.е. не содержать констант, определенных в частных случаях при конкретном выборе системы единиц измерения. Замена единиц измерения параметров в уравнении процесса не должна приводить к изменению вида уравнений.
Выявление подобных процессов разнородных физических подсистем производится на основе теорем подобия: первая и вторая теоремы подобияуказывают на существование определенных соотношений между параметрами подобных процессов —критериев подобия, а третья теорема вместе с дополнительными положениями к ней устанавливает необходимые и достаточныеусловия подобия.
При определении критериев подобия исходное уравнение можно разделить на любой из членов и получить различные формы записи критериев. Каждое слагаемое после этого становится критерием подобия. В критериях подобия знаки интегралов и дифференциалов исключаются. Критериями подобия будут также аргументы трансцендентных функций. Комбинации критериев подобия, полученные умножением, делением, возведением в степень и умножением на постоянный коэффициент тоже являются критериями подобия. Другой способ определения критериев подобия основывается на анализе размерностей и не требует записи уравнения процесса.
Теоремы подобия имеют следующие формулировки [12].
Первая теорема.У подобных процессов критерии подобия численно одинаковы.
Вторая теорема.Всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено в виде зависимости между критериями подобия.
Третья теорема.Необходимыми и достаточными условиями подобия являются равенство определяющих критериев подобия и пропорциональность сходственных величин, входящих в условия однозначности.
Третья теорема устанавливает для доказательства подобия жесткие требования аналогичности математических записей уравнений процессов, что обеспечивает одинаковое число и возможные формы записи определяющих критериев подобия. Условия однозначности в макромоделировании включают начальные и граничные условия.
Рассмотрим более подробно компонентные уравнения, связывающие разнородные фазовые переменные в элементах различных подсистем.
