3. Инженерный синтез корректирующего фильтра

В случае минимально-фазовых цепей задачу инженерного синтеза РАС удобно решать с помощью диаграмм Боде (асимптотические ЛАЧХ и ЛФЧХ). При синтезе РАС кроме заданных параметров обычно также известны объект управления, исполнительное устройство, устройство сравнения – эти устройства составляют неизменяемую часть системы.

На основании требований к точности РАС и параметров качества переходного процесса задаются требования к желаемой ЛАЧХ.

При этом задача синтеза сводится к проектированию корректирующего устройства (фильтра), позволяющего получить необходимые параметры качества РАС (запас устойчивости, рабочая полоса частот, время установления переходного процесса и т. п.).

Для определения ЛАХЧ корректирующего устройства необходимо из желаемой ЛАЧХ вычесть ЛАЧХ неизменяемой части системы.

Полученную ЛАЧХ аппроксимируют отрезками прямых линий с наклонами ± m20 дБ/декаду (± m6 дБ/октаву), где т – натуральное число (0, 1, 2, ...). Перпендикуляры, опущенные из точек сопряжения асимптот на ось частот, позволяют определить частоты сопряжения, а затем постоянные времени звеньев.

Рассмотримпример синтеза схемы по заданной асимптотической ЛАЧХ по следующим исходным данным (аналогично табл. 3.1): L(0) = 60 дБ, _с1 = 10, _с2 = 100, _с3 = 3000 (рад/с), наклон ЛАЧХ на участке до _с1 = – 20 дБ/дек, на участке _с1 – _с2 = = – 40 дБ/дек, _с2 – _с3 = – 20 дБ/дек, и после _с3 = – 40 дБ/дек).

Построенная по исходным данным асимптотическая ЛАЧХ приведена на рисунке 3.1.

Сначала необходимо разбить ЛАЧХ на элементарные участки, которым можно будет поставить в соответствие типовые динамические звенья первого и второго порядков (прил. 2).

Возможно несколько вариантов разбиения системы на элементарные звенья.

Например, можно взять идеальный интегратор, форсирующее и два инерционных (интегрирующих с запаздыванием) звена.

Но лучше выбрать вариант с меньшим числом звеньев.

На рисунке 3.2 приведены ЛАЧХ трех динамических звеньев, каскадное соединение которых дает заданную ЛАЧХ: два звена интегрирующих с запаздыванием (1 с _с1 и 3 с _с3) и одно изодромное (2 с _с2 ).

ПФ каскадного соединения звеньев (k₀ = k₁ k₂ k₃):

. (3.1)

Сучетом соотношения между постоянной времени и частотой сопряжения звена

T_i = 1/_{с i}

получаем

T₁ = 1/10 = 0,1 с, T₂ = 1/100 = 0,01 с, T₃ = 1/3000 = 0,33 мс.

На рисунке 3.3 сплошной линией приведена ЛАЧХ синтезированной схемы. Штриховой линией на рисунке 3.3 показана заданная асимптотическая ЛАЧХ. Отклонения асимптотической ЛАЧХ от точной в области частот среза не превышают 3 дБ.

Н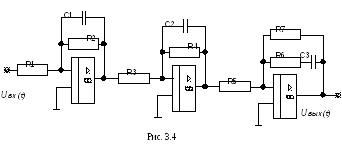а основании ПФ (3.1) и данных рис. 3.2 получаем электрическую схему (рис. 3.4).

Распределим общий КУ (60 дБ) равномерно по всем каскадам:

k₁ = k₂ = k₃ = 10 (20 дБ).

Определим номиналы элементов схемы с учетом рядов стандартных значений.

R₂C₁ = T₁ = 0,1 с, пусть C₁ = 1 мкФ, тогда R₂ = 100 кОм, а R₁ = 10 кОм.

R₄C₂ = T₃ = 0,33 мс, пусть C₂ = 0,033 мкФ, тогда R₄ = 100 кОм, а R₃ = 10 кОм.

R₆C₃ = T₂ = 0,01 с, пусть C₃ = 10 мкФ, тогда R₆ = 1 кОм, R₇ = 100 кОм, а R₅ = 10 кОм.

Сопротивление R₇ в изодромное звено введено для получения необходимого коэффициента передачи по постоянному напряжению. Повышая R₇ со 100 до 150 кОм отклонение ЛАЧХ от заданной на  = 1 можно снизить до 1 дБ, но в данном случае в этом нет необходимости.

При применении инверсии фазы в одном или трех каскадах график ЛФЧХ сместится на 180 вниз, и соответственно изменятся запасы устойчивости.

При практической реализации схемы (рис. 3.4) следует выбирать включение и цепи коррекции операционных усилителей так, чтобы каждый каскад оставался устойчивым.

На рисунке 3.5 сплошной линией приведена ЛАЧХ синтезированной схемы.

Отклонения от заданной (штриховая линия на рис. 3.5) максимальны на  < 1 и не превышают 3 дБ.

На рисунке 3.5 также приведена ЛФЧХ системы и определены запасы устойчивости по усилению и фазе:

L_З = 130 дБ, _З = 55.

Запасы устойчивости достаточны.

На рисунке 14 изображены графики ПХ и ИХ.

Взадании № 3 необходимо спроектировать корректирующий фильтр по заданной асимптотической ЛАЧХ.