1. Пф Kyx(p) в операторной форме отражает способность звена преобразовывать входное воздействие

. (1.2)

где L – оператор прямого преобразования Лапласа (прил. 1).

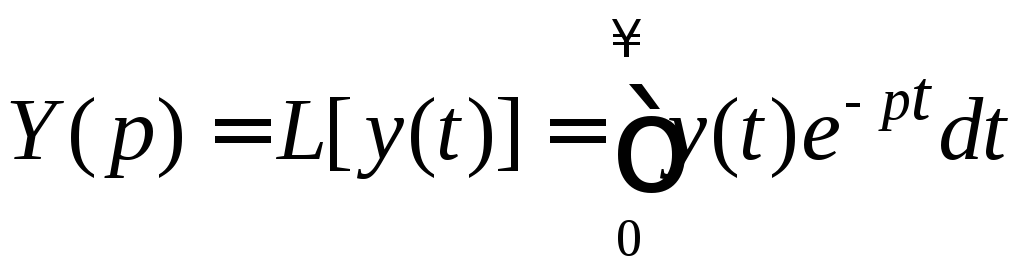, (1.3)

есть прямое преобразование Лапласа выходного процесса.

От ПФ в операторной форме в стационарном режиме можно перейти к частотной ПФ (ЧПФ), заменив оператор p на переменную i, где – мнимая единица.

. (1.4)

Y(i) – спектральная характеристика выходного процесса, полученная как прямое преобразование Фурье F[y(t)] от временной функции y(t)

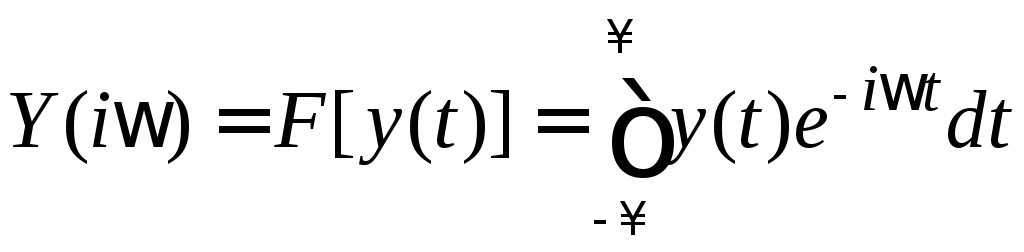. (1.5)

ЧПФ есть комплексный коэффициент передачи системы по частоте .

Частотные свойства ЧПФ отображают также в виде графика – годографа. Годограф ЧПФ строят либо в полярной, либо в декартовой системе координат. При этом соответственно пользуются экспоненциальной или алгебраической формами записи комплексного числа

. (1.6)

Соответствующий график содержит информацию о модуле – K_yx(ω), фазе – φ_yx(ω) и циклической частоте ω. Так как каждая его точка соответствует определенной фиксированной частоте, его называют амплитудно-фазово-частотной характеристикой (АФЧХ).

Амплитудно-частотная характеристика (АЧХ) строится по формуле

, (1.7)

где Y(ω) и X(ω) – комплексные амплитуды процессов на частоте ω.

Фазово-частотная характеристика (ФЧХ) представляется в виде

. (1.8)

Графики АЧХ и ФЧХ имеют линейный масштаб по оси абсцисс.

Временные характеристики. T – постоянная времени цепи, которая характеризует быстродействие звена, ее можно определить графически, если провести касательную к кривой h(t) (ПХ) в точке h(0) (рис. 1.1).

Д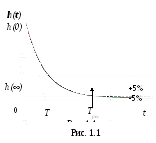ля звеньев первого порядка время регулирования может быть определено какT_pег= (4...5)T [1].

При исследовании ПХ динамических звеньев в виде электрических цепей создать единичный скачок напряжения несложно. Для этого, в частности, можно использовать периодическую последовательность прямоугольных импульсов, длительность которых будет существенно больше T_pег звена.

Амплитуда импульсов должна выбираться с таким расчетом, чтобы не нарушились условия линейности звена.

Импульсная характеристика (ИХ) – g(t) определяет поведение процесса на выходе системы при воздействии на ее входе дельта-импульса ((t) – функции Дирака) при нулевых начальных условиях.

– (1.9)

обратное преобразование Лапласа ПФ K(p); а

– (1.10)

обратное преобразование Фурье ЧПФ K(i).

ИХ, как и ПХ h(t), АФЧХ, совокупность ЛАЧХ и ЛФЧХ, также позволяет определить все параметры линейного звена.

В условиях эксперимента можно сформировать воздействие (t) лишь приближенно, например использовать короткий импульс, длительность которого много меньше постоянной времени звена (Т_и << Т). Рекомендуется выбирать Т_и из отношения Т_и < Т/(20…50).

Взаимосвязь динамических характеристик

Выходное воздействие можно представить в виде

• дифференциального уравнения;

• операторного коэффициента передачи (изображение по Лапласу);

• комплексного коэффициента передачи (изображение по Фурье);

• переходной (ПХ) или импульсной характеристики (ИХ).

ПФ K(p), частотные и временные характеристики линейных звеньев или систем между собой связаны (табл. 1.1).

Таблица 1.1

Передаточные функции, временные характеристики	K(p)	K(i)	g(t)	h(t)
K(p)	–	K(i)|i=p
K(i)	K(p)|p=i	–	F[g(t)]
g(t)			–
h(t)				–

В силу взаимосвязи этих характеристик вычисление выходной величины может быть выполнено различными способами:

. (1.11)

Логарифмические частотные характеристики

В инженерной практике часто пользуются логарифмическими эквивалентами АЧХ и ФЧХ: логарифмической амплитудно-частотной характеристикой (ЛАЧХ)

(1.12)

и логарифмической фазово-частотной характеристикой (ЛФЧХ)

. (1.13)

По оси абсцисс значения  (или f – Гц) откладываются в логарифмическом масштабе. Основные деления сетки частоты отличаются на декаду (в 10 раз). При этом обычно пересечение осью ординат оси абсцисс выбирают в значении 1 рад/с (1Гц).

В отличие от АЧХ, имеющей линейный масштаб изменения коэффициента передачи, изменение ординаты ЛАЧХ линейно по отношению к приращению функции в дБ.

По оси ординат графиков ФЧХ и ЛФЧХ фаза откладывается в градусах либо в радианах. Масштаб линейный. Отличие их в масштабе по оси абсцисс. В первом случае он линейный, во втором – логарифмический. Таким образом, и ЛЧХ, и ЛФЧХ – полулогарифмические характеристики.

На рисунке 1.2 (графики 1) приведены графики ЛАЧХ и ЛФЧХ для ЧПФ при k₀ = 100 (40 дБ), Т₁ = 0,1 с, Т₂ = 0,01 с

Экспериментально ЛАЧХ и ЛФЧХ исследуются в установившемся режиме. При этом на вход звена или системы подают гармоническое воздействие с постоянной амплитудой x(t)=X₀sin( t), частота  изменяется либо дискретно, либо непрерывно, например, по линейному закону. В последнем случае изменения частоты должны быть медленнее наибольшей постоянной времени РАС.

Е

Рис. 1.2

сли необходимый диапазон частот гармонического воздействия заранее неизвестен, его стараются выбирать не уже интервала, в пределах которогоL() превышает уровень – 40дБ. Интервал частот выбран правильно, если за его пределами фаза коэффициента передачи изменяется не более чем на 6°. Логарифмические частотные характеристики – очень удобный и наглядный инструмент анализа и синтеза линеаризованных систем.

Асимптотические ЛАЧХ и ЛФЧХ. В инженерной практике применяют приближенные эквиваленты ЛАЧХ и ЛФЧХ – асимптотические логарифмические частотные характеристики.

Для построения асимптотической ЛАЧХ динамического звена прежде всего следует выяснить тип звена, определить пределы изменения частоты, коэффициент передачи на постоянном токе и частоты сопряжения.

Пределы изменения частоты  достаточно ограничить интервалом

f_min/30 = 1/30Т_max ... 30 f_max = 30/T_min , (1.14)

где Т_min и Т_max – соответственно, наибольшее и наименьшее значения постоянных времени звена.

Частоты сопряжения находят через постоянные времени звена (_j = 1/Т_j). ЧПФ необходимо свести к виду (1.15), для этого числитель и знаменатель представляют в виде произведения множителей вида (1 + iТ_j).

Если такой множитель будет в знаменателе, его асимптотическая ЛАЧХ до частоты сопряжения _j имеет постоянную асимптоту ЛАЧХ 0 дБ, после _j асимптота линейно убывает со скоростью – 20 дБ/дек (дБ на декаду или – 6 дБ на октаву); а ЛФЧХ до частоты сопряжения _j будет примерно равна 0, после _j – примерно – 90, на частоте _j = – 45.

Если множитель (1 + iТ_j) окажется в числителе, его асимптотическая ЛАЧХ до частоты сопряжения _j будет постоянной на уровне 0 дБ. После _j асимптота линейно будет возрастать со скоростью + 20 дБ/дек, а ЛФЧХ до частоты сопряжения _j будет примерно равна 0, после _j – примерно + 90, на частоте _j = + 45.

На рисунке 1.2 (графики 2) построены асимптотические ЛАЧХ и ЛФЧХ. Для их построения необходимо найти частоты сопряжения ₁ = 1/Т₁ = 10 рад/с, ₂ = 1/Т₂ = 100 рад/с.

Звено в числителе (форсирующее – классификацию звеньев см. в п. 2.4, а также прил. 2) до частоты ₂ имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно возрастает со скоростью + 20 дБ/дек.

Звенья в знаменателе: первое (идеальный интегратор) дает асимптоту ЛАЧХ, которая начинается на уровне + 40 дБ (k₀) при  = 1 и убывает со скоростью – 20 дБ/дек; второе (апериодическое) до частоты ₁ имеет постоянную асимптоту ЛАЧХ 0 дБ, а после нее асимптота линейно убывает со скоростью –20 дБ/дек.

После суммирования асимптотических ЛАЧХ звеньев получим итоговую асимптотическую ЛАЧХ (рис. 1.2 график 2).

Максимальная погрешность асимптотической ЛАЧХ получается на частотах сопряжения и не превышает 3 дБ.

Для минимально фазовых цепей достаточна грубая оценка ЛФЧХ. Итоговая асимптотическая ЛФЧХ (рис. 1.2 график 2) получается суммированием ЛФЧХ звеньев: интегрирующее звено имеет постоянный фазовый сдвиг – 90, фаза звена первого порядка изменяется с ростом  от 0 до – 90 (апериодическое) или от 0 до + 90 (форсирующее), проходя на частотах сопряжения через значение  45.

Динамическое звено – элемент системы, обладающий свойствами однонаправленности и независимости. Число динамических звеньев структурной схемы определяется удобством математического описания РАС.

На практике ПФ РАС представляет собой произведение передаточных функций динамических звеньев, порядок полинома ПФ которых не выше второго.

K(p)= , (1.15)

где Т – постоянная времени звена, с;  – коэффициент демпфирования (обратная величина добротности) системы; v – количество интеграторов (показатель астатизма системы). В числителе (1.15) собираются множители с опережением по фазе, в знаменателе (1.15) – с отставанием по фазе.

Динамические звенья разделяют на интегрирующие, дифференцирующие и позиционные звенья. Характеристики элементарных звеньев (схема, ПФ, ПХ, ИХ) приведены в приложении 2.

К позиционным звеньям относятся

• звенья пропорционального регулирования (ПФ );

• апериодические (ПФ ,  < _с1);

• колебательные (ПФ );

• безынерционные (ПФ K(p) = k₀).

К интегрирующим звеньям относятся

• идеальные интеграторы (ПФ );

• инерционные интеграторы (ПФ );

• замедляющие (апериодические) (ПФ ,  > _с1) и

• изодромные (ПФ ) звенья.

К дифференцирующим звеньям относятся

• идеально дифференцирующие (K(p) = k₀p);

• дифференцирующие с замедлением (ПФ ) и

• форсирующие звенья (ПФ K(p) = k₀(1+Tp)) .

Для звена с чистым запаздыванием на время : K(p) = e^–pτ  f(t–τ) .