2. Особенности звеньев второго порядка

Р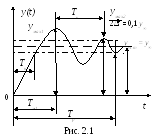азличают прямые и косвенные оценкипоказателей качества переходного процесса. Прямые оценки получаются по аналитической или экспериментальной временной характеристике (обычно ПХ). Косвенные оценки получаются обычно по частотным характеристикам (АХЧ, резонансная частота контура, добротность и т.п.).

Прямые оценки качества переходного процесса

К основным показателям качества ПХ относятся следующие параметры (рис. 2.1):

1. у_∞ = у_уст – установившееся значение ПХ.

2. Т_м1 – время установления первого максимума.

3. γ – величина перерегулирования:

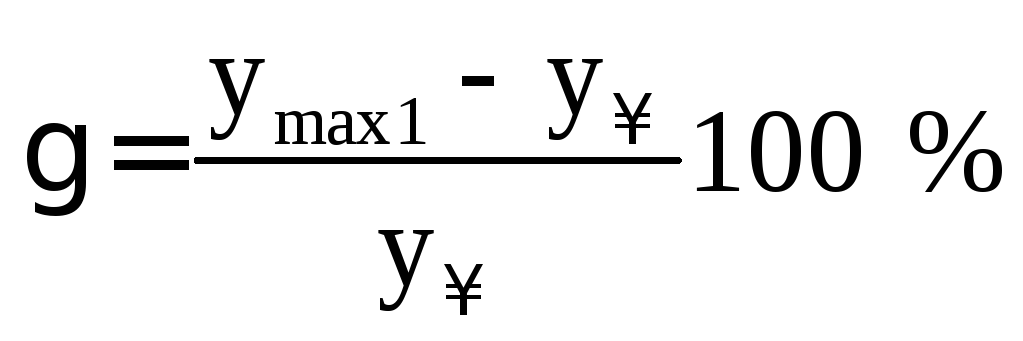. (2.1)

4. Т_р – время регулирования .

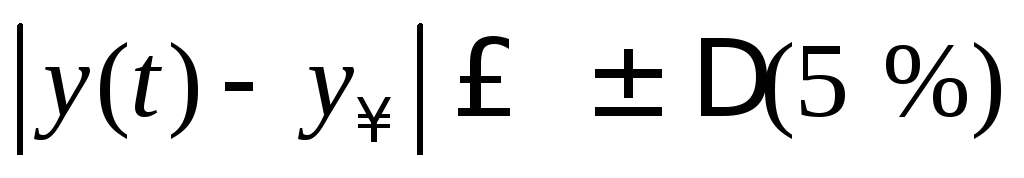Время регулирования – это минимальное время от начала переходного процесса до момента времени, после которого отклонение выходного процесса от установившегося значения у_уст не превышает заданного значения (обычно  5 %).

5. Т_к – период или частота колебаний (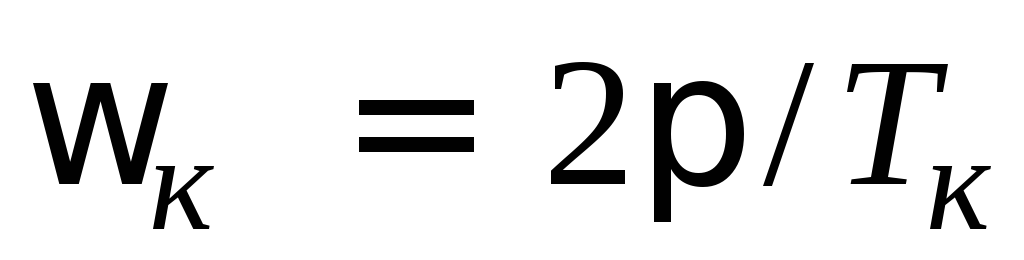) в переходном процессе.

6. Декремент затухания .

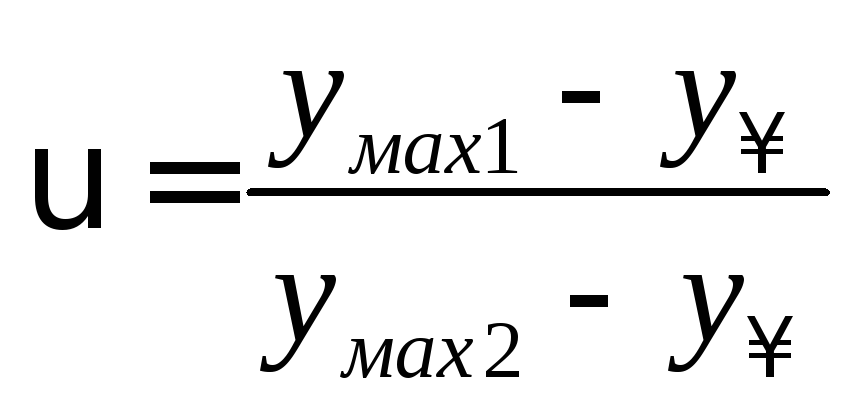7. Количество перерегулирований N – количество превышений уровня у_∞ за время Т_р..

Иногда также оценивают время нарастания ПХ Т_н (Т_н на рис. 2.1), а также время запаздывания Т_зап – время, при котором ПХ достигает уровень 0,5у_уст.

Косвенные оценки качества переходного процесса

К косвенным показателям качества переходного процесса относят частотные, корневые и интегральные оценки [1, 10].

Ч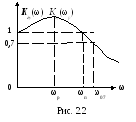аще всего используютсячастотные показатели качества, которые определяют по АХЧ замкнутой системы (K_λy(ω) и т. д.), ЛФЧХ и ЛАЧХ разомкнутой системы и по вещественной части P(ω) ЧПФ замкнутой системы.

Частотная характеристика астатической системы представлена на рисунке 2.2.

К частотным показателям качества относятся.

1. Полоса пропускания ω_п – полоса частот, в которой АЧХ превышает единицу. У астатической РАС ω_п = ω_ср. Если АЧХ во всем диапазоне частот меньше единицы, то ω_п отсчитывается по уровню 0,71. В этом случае ω_п = ω₀₇, где ω₀₇ – полоса пропускания РАС по уровню 0,71 (половинной мощности).

2. ω₀ – резонансная частота, которая отсчитывается по максимуму АЧХ замкнутой системы и определяет частоту колебаний ω_к в переходном режиме. При такой АЧХ полосу пропускания ω_п правильнее оценивать по уровню 0,71 (– 3 дБ) от максимального значения АЧХ.

3. Частота среза АЧХ (ЛАЧХ) разомкнутой системы ω_ср.

4. Показатель колебательности М – отношение максимального значения АЧХ K_λy(ω_р) к значению на постоянном токе K_λy(0):

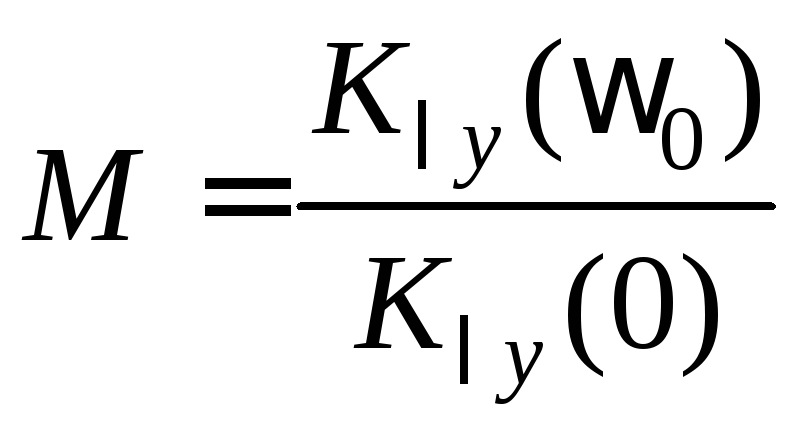. (2.2)

Обычно желательно иметь М ≤ 2.

При М > 1,5 – ПХ имеет колебательный характер (N  2),

если 1,1 < М < 1,5, то ПХ имеет малоколебательный характер (N < 2),

при М ≤ 1 характер ПХ будет апериодическим.

Рассмотрим связь некоторых частотных показателей качества с основными показателями качества быстродействия РАС.

Время регулирования Т_р можно оценить по формуле

. (2.3)

Существует связь между показателем колебательности М и запасом устойчивости по фазе φ_з.

. (2.4)

Временные и частотные характеристики звеньев второго порядка

ПФ звена второго порядка можно представить в нескольких формах за-писи:

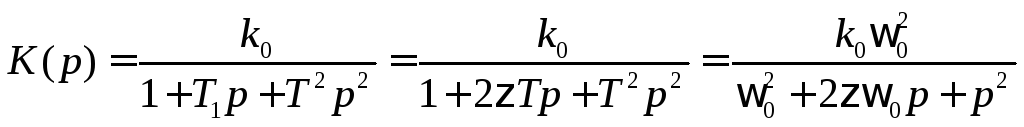, (2.5)

г

-5%

k₀

h(t)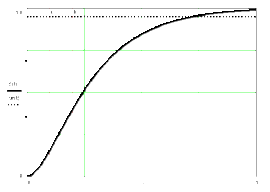

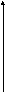
де– коэффициент демпфирования. Возможно представление ПФ в виде

k₀/2

. (2.6)

Н

Т₃ Т₄

Т_р

Т_зап

0

аиболее общие формы – первая и вторая в (2.5). Третьей в (2.5) пользуются преимущественно для колебательных звеньев.

Ф

t

Рис. 2.3

орма (2.6) удобна исключительно для апериодических звеньев.

Свойства апериодического и колебательного позиционных звеньев отличаются прежде всего разными значениями величин .

Для апериодических звеньев второго порядка   1. Для них характерна монотонная форма ПХ и плавная, без подъемов, АЧХ (ЛАЧХ), имеющая в области высоких частот крутизну спада 40 дБ/декаду (прил. 2).

ПХ такого звена определяется по формуле (прил. 1)

, (2.7)

а ИХ – как

. (2.8)

График ПХ h(t) (рис. 2.3) дает представление об определении параметров ПФ по экспериментальной характеристике.

(См. также рис. 2.4 и 2.5, график 4.)

Если в (2.6) – (2.8) Т₃ = Т₄ ( = 1 или Т₁ = 2Т₂ в (2.5)), то

, . (2.9)

При Т₄  0 звено вырождается в апериодическое звено первого порядка.

У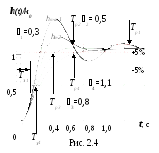колебательного звена < 1.

Если параметр демпфирования  лежит в пределах , то на ПХ (рис. 2.4, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 2.5) по существу не меняется.

По мере уменьшения ярче проявляются резонансные свойства звена (рис. 2.5, графики 1 и 2), и соответственно увеличивается колебательность временных характеристик (число пересечений уровня h() (рис. 2.4, графики 1 и 2) и g().

Хотя при увеличении  уменьшается время запаздывания (Т_З1 – Т_З4 на рис. 2.4) и увеличивается максимальная скорость нарастания ПХ 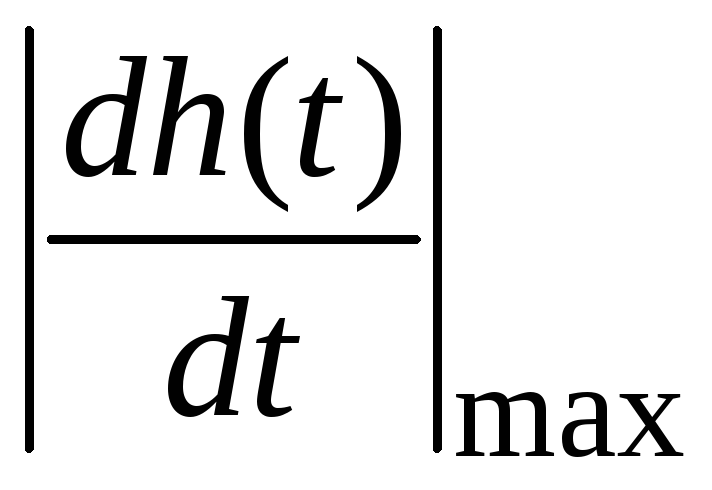, время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 2.4 Т_Р1 > Т_Р2 > Т_Р3 < Т_Р4 ).

Число полных периодов колебаний N за время регулирования (N = 1 на ПХ рис. 2.6, N = 2 на ПХ рис. 2.4, график 1).

Временные характеристики колебательного звена описываются выражением

=

= , (2.10)

. (2.11)

В (2.10) – (2.11) – собственная частота колебаний звена; – коэффициент затухания; также a и _к являются соответственно действительной и мнимой частями корней характеристического уравнения звена ():

. (2.12)

Г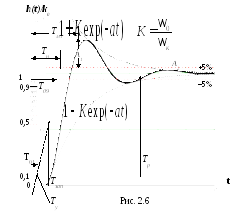рафики звена второго порядка с колебательной ПХ изображены на рисунках 2.4 и 2.6.

График на рисунке 2.6 иллюстрирует, как по экспериментальной ПХ реального звена можно найти параметры соответствующего колебательного звена.

Если параметр демпфирования  лежит в пределах , то АЧХ по существу не меняется (рис. 2.5) по сравнению с апериодическим звеном (  1), хотя на ПХ (рис. 2.4, график 3) появляется выброс.

Только в случае наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением . Обычно резонансная частота ₀ несколько ниже _к, но приближается к ней с ростом  (рис. 2.5).

На рисунке 2.7 приведены примеры нормированных АЧХ звеньев второго порядка: апериодического (график 1) и колебательного (график 2).