
Matem_Lisitsya_2
.pdf
41
Якщо функція F ( x) є первісною для для f ( x) , то вираз F ( x) + C , де C –
довільна стала величина, називається невизначеним інтегралом від функції f ( x) і позначається символом ∫ f ( x)dx .
Таким чином, за означенням:
∫ f ( x)dx = F ( x) + C , якщо F ′( x) = f ( x) .
При цьому функцію f ( x) називають підінтегральною функцією, f ( x)dx
– підінтегральним виразом, знак ∫ – знаком інтеграла.
Таблиця найпростіших інтегралів
1. |
∫ xα dx = |
|
|
xα +1 |
|
+ C, α ≠ −1; |
|
|
|
|
|
|
|
|
2. ∫ |
dx |
|
|
|
|
+ C ; |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
= ln |
|
x |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
α + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x − a |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3. |
|
|
|
dx |
|
|
= |
|
1 |
arctg |
x |
|
+ C = − |
1 |
arcctg |
x |
+ C , |
a ≠ 0 |
; 4. |
|
|
|
|
dx |
|
= |
1 |
|
|
+ C, a ≠ 0 ; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
||||||||||||||||||||||||||||||||||||||
|
∫ x 2 + a 2 |
|
|
|
|
|
|
a |
|
|
|
a |
a |
|
|
a |
|
1 |
|
|
∫ x 2 − a 2 |
|
|
|
|
2a |
x + a |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
5. |
∫ |
|
|
dx |
|
|
= |
1 |
|
|
a + x |
|
+ C, a ≠ 0 ; |
|
|
|
|
|
|
6. ∫a x dx = |
a x |
+ C, a > 0 ; |
||||||||||||||||||||||||||||||
|
|
|
|
|
ln |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
a |
2 |
2 |
|
|
|
a − x |
|
|
|
|
|
|
ln a |
|||||||||||||||||||||||||||||||||||||||
|
|
|
− x |
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∫ |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. ∫e x dx = e x + C ; |
|||||||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
= ln |
x + x 2 + a |
+ C, a ≠ 0 ; |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
+ a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
9. |
∫ |
|
|
dx |
|
|
|
|
|
= arcsin |
x |
+ C = − arccos |
x |
+ C , |
|
a ≠ 0 ; |
10. |
|
∫ |
sin xdx = − cos x + C ; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
a 2 |
− x 2 |
|
|
|
|
a |
|
|
a |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
11. ∫cos xdx = sin x + C ; |
|
|
|
|
|
|
|
|
12. ∫ |
|
|
dx |
|
|
|
= tgx + C ; |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos |
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||
13. ∫ |
|
dx |
|
|
|
= −ctgx + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
sin |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Основні правила інтегрування
1. Якщо F ′( x) = f ( x) , то ∫ f ( x)dx = F ( x) + C , де С – довільна стала.
2.∫ A f ( x)dx = A ∫ f ( x)dx , де А – стала величина.
3.∫( f1 ( x) ± f 2 ( x))dx = ∫ f1 ( x)dx ± ∫ f 2 ( x)dx .
4.Якщо ∫ f ( x)dx = F ( x) + C та u = ϕ ( x) , то ∫ f (ϕ ( x)) ϕ ′( x)dx = ∫ f (u)du = F (u) + C .
42
5. Інтегрування частинами. Якщо u = ϕ ( x) та v = ψ ( x) – функції, які мають
похідні, то ∫udv = u v − ∫vdu . |
|
|
|
|
|
|
|
|
|
|
Визначений інтеграл |
|
|
|
|
|
|
||
Нехай |
на відрізку [a, b] задано неперервну |
функцію |
f ( x) . |
Розіб’ємо |
|||||
відрізок [a, b] на n частин точками ділення |
|
|
|
|
|
|
|
||
a = x0 , x1 , x2 ,..., xn = b , причому x0 < x1 < x2 < ... < xn , і покладемо, що |
|
|
|||||||
x1 − x0 = |
x1 , x2 − x1 = x2 ,..., xn − xn−1 = xn . |
На |
кожному |
|
з |
|
відрізків |
||
[x0 , x1 ], [x1 , x2 ],..., [xn−1 , xn ] візьмемо по точці ξ1 , ξ2 ,..., ξn . Складемо суму |
|
|
|
||||||
|
|
n |
|
|
|
|
|
|
|
Sn = f (ξ1 ) x1 + f (ξ2 ) x2 + ... + f (ξn ) xn = ∑ f (ξi ) xi . |
|
|
|
|
|
|
|||
|
i =1 |
|
|
|
|
|
|
|
|
Якщо при будь-яких розбиттях відрізка [a, b] таких, що max |
xi |
→ 0 , і при |
|||||||
|
n |
|
|
|
|
|
|
|
|
будь-якому виборі точок ξi сума ∑ f (ξi ) |
xi |
прагне до однієї і тієї ж границі I, |
|||||||
|
i =1 |
|
|
|
|
|
|
|
|
то функція |
f ( x) називається інтегрованою на відрізку [a, b], |
а границя I – |
|||||||
визначеним інтегралом від функції f ( x) |
на відрізку [a, b]. |
|
|
|
|
|
|||
|
|
|
b |
|
|
|
|
|
|
Визначений інтеграл позначають |
як ∫ f (x)dx . Число |
a називається |
|||||||
|
|
|
a |
|
|
|
|
|
|
нижньою границею інтеграла, b – верхньою границею, відрізок |
[a, b] |
– |
|||||||
відрізком інтеграції, x – змінною інтеграції. |
|
|
|
|
|
|
|||
|
Формула Ньютона-Лейбниця |
|
|
|
|
|
|||
Якщо |
b |
|
|
Функція |
F ( x) |
– |
первісна |
||
F ( x) = f ( x) , то ∫ f (x) dx = F (b) − F (a) . |
|||||||||
|
′ |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
функції f ( x) . |
|
|
|
|
|
|
|
|
|
|
Заміна змінної у визначеному інтегралі |
|
|
|
|
|
|||
Якщо функція f ( x) неперервна на відрізку a ≤ x ≤ b та x = ϕ (t) |
– функція, |
||||||||
неперервна разом зі своєю похідною ϕ ′( x) |
на відрізку α ≤ t ≤ β , |
де a = ϕ (α ) |
та |
||||||
b |
β |
|
|
|
|
|
|
|
|
b = ϕ (β ) , то ∫ f (x) dx = ∫ f (ϕ (t )) ϕ ′(t) dt . |
|
|
|
|
|
|
|
|
|
a |
α |

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|||
Приклад: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обчислити інтеграл ∫ |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 + x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Зробимо |
|
|
заміну |
змінної: x = t 2 , |
|
тоді |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dx = 2tdt , |
t = x , t = |
x = 0 = 0 , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
= 2 . Обчислимо інтеграл з урахуванням заміни: |
|
|
|
|
||||||||||||||||
t 2 |
= |
x2 = |
4 |
|
|
|
|
|||||||||||||||||||||||
4 |
|
dx |
|
|
|
|
2 |
2tdt |
2 |
(t + 1 − 1)dt |
|
2 |
2 |
dt |
|
2 |
d (t + 1) |
|
|
|
|
|
|
|
||||||
∫ |
|
|
|
= |
∫ |
= 2∫ |
|
|
= 2∫dt − 2∫ |
= 2(2 − 0) − 2∫ |
= |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0 1 + x |
0 1 + t |
0 |
t + 1 |
0 |
0 |
t + 1 |
|
0 |
t + 1 |
|
|
|
|
|||||||||||||||||
= 4 − 2(ln 3 − ln1) = 4 − 2 ln 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площі плоских фігур |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Якщо неперервна крива задана у прямокутних координатах рівнянням |
||||||||||||||||||||||||||
y = f ( x) , |
причому |
f ( x) ≥ 0 , |
то площа криволінійної трапеції, яка обмежена цією |
|||||||||||||||||||||||||||
кривою, |
двома вертикальними прямими |
|
x = a та x = b і відрізком осі абсцис |
|||||||||||||||||||||||||||
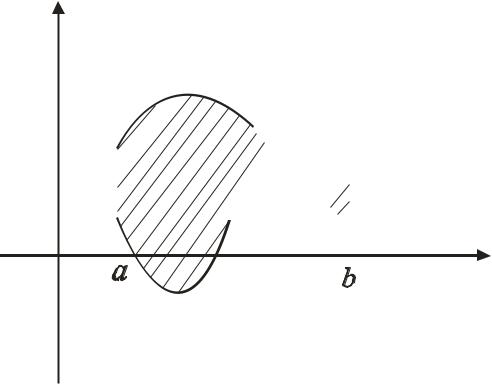
b
a ≤ x ≤ b (Рис. 6), визначається за формулою: S = ∫ f (x)dx.
a
Y
y=f(x)
S
O
X
Рис. 6
44
У загальному випадку, коли площа S обмежена двома неперервними кривими y = f1 (x) та y = f 2 (x) і двома вертикальними прямими x=a та x =b, де
b
f1 ( x) ≤ f 2 ( x) при a ≤ x ≤b (Рис. 7), то будемо мати формулу: S = ∫( f2 (x) − f1(x)) dx.
a
Y
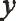 = f2 ( x)
= f2 ( x)
 S
S

O |
X |
 = f1 ( x )
= f1 ( x )
Рис. 7.
Диференціальні рівняння
Диференціальним рівнянням називається рівняння, яке зв’язує незалежну змінну x, шукану функцію y = f ( x) та її похідні y′, y′′,..., y(n ) .
У загальному вигляді диференціальне рівняння можна записати таким чином: F (x, y, y′, y′′,..., y ( n) ) = 0 .
Порядком диференціального рівняння називається порядок найвищої похідної, яка входить у рівняння.

45
Рішенням, або інтегралом диференціального рівняння називається будьяка функція y = f ( x) , яка, будучи підставленою у рівняння, перетворює його у
тотожність.
Диференціальні рівняння першого порядку зі змінними, які
відокремлюються.
Диференціальним рівнянням зі змінними, які відокремлюються, називається рівняння першого порядку, яке має вигляд:
y′ = f ( x) g ( y) , або |
f1 ( x) g1 ( y) dx + f 2 ( x) g 2 ( y) dy = 0 . |
|||||||
Якщо візьмемо до уваги, що y′ = |
dy |
, то перше рівняння можемо записати |
||||||
|
||||||||
|
|
|
|
|
|
dx |
||
таким чином: |
dy |
|
= f ( x) |
dx . Рішення цього рівняння (загальний інтеграл) |
||||
|
|
|||||||
|
|
|||||||
|
g ( y) |
|
|
|
||||
знаходимо у вигляді ∫ |
dy |
= ∫ f (x)dx + C . |
||||||
g ( y) |
||||||||
|
|
|
|
|
|
|
||
У другому випадку розділимо обидві частини рівняння на f 2 (x) g1 ( y) і |
||||||||
отримаємо |
f1 ( x) |
dx + |
g 2 |
( y) |
dy = 0 . Проінтегруємо останнє рівняння і отримаємо |
|
|
|
|||
|
f 2 ( x) |
|
g1 |
( y) |
|
рішення диференціального рівняння у вигляді: ∫ f1 ( x) f 2 (x)
dx + ∫ g 2 ( y) dy = C . g1 ( y)
Лінійні диференціальні рівняння першого порядку
Диференціальні рівняння, які мають вигляд y′ + f ( x) y = g ( x) називаються лінійними диференціальними рівняннями першого порядку. Якщо g ( x) = 0 , то рівняння матиме вигляд y′ + f ( x) y = 0 і називається однорідним лінійним диференціальним рівнянням. У цьому випадку маємо диференціальне рівняння
зі змінними, які відокремлюються: dy = − f (x)dx . Знаходимо y
або y = Ce−∫ f ( x)dx , де C = eC1 .
Для вирішення неоднорідного лінійного рівняння використовуємо так званий метод варіації довільної сталої. Цей метод полягає в тому, що спочатку
46
знаходимо загальне рішення відповідного однорідного лінійного рівняння у
вигляді y = Ce−∫ f ( x)dx . Потім вважаємо, що C є функція від змінної x : C = C(x) .
Таким чином, шукаємо загальне рішення неоднорідного рівняння у вигляді
−∫ f ( x)dx |
Знаходимо |
|
′ |
′ |
−∫ f ( x)dx |
|
−∫ f ( x)dx |
Підставимо |
||
y = C(x)e |
. |
y |
|
= C (x)e |
|
− C(x) f (x)e |
. |
|||
y = Ce−∫ f ( x)dx |
та |
знайдене |
y′ |
|
у рівняння |
|
y′ + f ( x) y = g ( x) і |
отримаємо |
||
|
|
|
|
|
′ |
−∫ f ( x)dx |
= g(x) . З останнього рівняння |
|||
диференціальне рівняння для C( x) : C (x)e |
|
|||||||||
знаходимо C = C( x) . |
|
|
|
|
|
|
|
|
||
Для вирішення рівняння |
|
y′ + f (x) y = g (x) можна |
також |
застосувати |
||||||
підстановку |
y = u(x) v(x) . |
Знаходимо |
y′ = u(x)′ v(x) + u(x) v′(x) . |
Підставимо |
||||||
y = u(x) v(x) |
та |
знайдене y′ |
у рівняння |
y′ + f (x) y = g (x) . |
Після |
перетворень |
||||
отримаємо таке рівняння: (u′(x) + f (x)u(x)) v(x) + v′(x)u( x) = g (x) (*). Функцію u( x)
знаходимо такою, щоб виконувалось рівняння u′ + f (x) u = 0 . Тоді рівняння (*)
матиме вигляд: v′ u = g (x) . З останнього рівняння знаходимо функцію v(x) і,
таким чином, функцію y = u(x) v(x) .
Лінійні диференціальні рівняння із сталими коефіцієнтами
Диференціальне рівняння, яке має вигляд:
y( n) + f ( x) y( n−1) + f |
2 |
(x) y( n−2) + ... + f |
n−1 |
( x) y′ + f |
n |
(x) y = g (x) |
|
|
||
1 |
|
|
|
|
|
|
|
|||
називається |
лінійним диференціальним |
рівнянням n-го порядку. Якщо |
||||||||
g ( x) ≡ 0 , то |
відповідне |
диференціальне рівняння називається однорідним. |
||||||||
Загальне рішення такого рівняння (загальний інтеграл) має вигляд: |
|
|||||||||
y = C1 y1 + C2 y2 + ... + Cn yn , |
де y1, y2 ,..., yn |
|
– лінійно |
незалежні |
рішення |
|||||
однорідного |
лінійного |
рівняння (фундаментальна |
система |
рішень), |
||||||
C1, C2 ,..., Cn – довільні сталі. Загальне рішення неоднорідного рівняння є сума загального рішення однорідного рівняння і будь-якого рішення (частинного рішення) неоднорідного рівняння, тобто:
y = C1 y1 + C2 y2 + ... + Cn yn + yч , де yч − частинне рішення неоднорідного рівняння.
|
47 |
У випадку, коли функції |
f1 ( x) ≡ A1,..., fn ( x) ≡ An – сталі, то |
диференціальне рівняння називається лінійним диференціальним рівнянням із
сталими |
коефіцієнтами, |
а |
коли |
g ( x) ≡ 0 |
− то |
однорідним |
лінійним |
|
диференціальним рівнянням із сталими коефіцієнтами. Рішення |
y1, y2 ,..., yn |
|||||||
знаходяться |
за |
допомогою |
характеристичного |
рівняння: |
||||
λn + A λn−1 |
+ ... + A |
λ + A = 0 : |
|
|
|
|
|
|
1 |
n−1 |
n |
|
|
|
|
|
|
1) |
Кожному дійсному |
кореню |
λ = a |
кратності |
m характеристичного |
|||
рівняння відповідають m незалежних рішень eax , xeax , ..., xm−1eax .
2) Кожній парі комплексних коренів λ = a ± bi кратності m відповідають m пар незалежних рішень:
|
ax |
ax |
cosbx,..., x |
m−1 |
ax |
cosbx, |
||
e |
cosbx, xe |
e |
|
|
||||
|
ax |
ax |
|
m−1 ax |
|
|
||
|
sinbx,..., x |
sinbx. |
||||||
e |
sinbx, xe |
|
e |
|
||||
У випадку лінійного однорідного рівняння другого порядку із сталими коефіцієнтами загальне рішення має один з трьох виглядів:
1) y = C1eλ1x + C2eλ2x , якщо λ1 та λ2 − дійсні і λ1 ≠ λ2 ;
2)y = eλ1x (C1 + C2 x) , якщо λ1 = λ2 ;
3)y = eax (C1 cosbx+ C2 sinbx) , якщо λ1 = a + bi і λ2 = a −bi ( b ≠ 0).
Частинне рішення yч лінійного неоднорідного рівняння y′′ + A1 y′ + A2 y = g ( x) може бути знайдено методом невизначених коефіцієнтів у
наступних простіших випадках: |
|
|
|
|
|
|||
1. g ( x) = e ax P ( x) , де P (x) − многочлен ступеня n. |
|
|
|
|||||
|
n |
n |
|
|
|
|
|
|
Якщо a − не корінь характеристичного рівняння, тобто a2 + A a + A ≠ 0, |
||||||||
|
|
|
|
|
|
|
1 |
2 |
то покладаємо |
y =eaxQ (x) |
, де |
Q (x) |
− многочлен ступеня |
n |
з невизначеними |
||
ч |
n |
n |
|
|||||
коефіцієнтами. |
Якщо |
a |
− |
корінь характеристичного |
|
рівняння, |
тобто |
|
a2 + A a + A = 0 |
, то покладаємо |
y = xr eaxQ (x) , де r |
− кратність кореня a ( r =1 |
|||
1 |
2 |
|
|
ч |
n |
|
або a = 2 ). |
|
|
|
|
|
|
2. |
g ( x) = e ax ( P ( x) cos bx + Q |
m |
( x) sin bx ) . |
|
||
|
|
n |
|
|
|
|
|
|
|
|
|
|
48 |
|
Якщо |
a ± bi не |
є корінь |
характеристичного рівняння, то покладаємо |
||
yч |
= e ax (S N ( x) cos bx + TN ( x) sin bx) , |
де |
S N ( x), TN ( x) − многочлени ступеня |
|||
N = max{n, m}. |
Якщо |
a ± bi − |
корінь характеристичного |
рівняння, то |
||
yч |
= x r e ax (S N ( x) cos bx + TN ( x) sin bx) , де |
r − кратність коренів a ± bi |
(для рівняння |
|||
другого порядку r = 1). |
|
|
|
|
||
У випадках, коли права частина лінійного неоднорідного рівняння не має жодного з вищевказаних виглядів, тоді для знаходження рішення цього рівняння можна скористатись більш загальним методом, який називається
методом Лагранжа, або методом варіації довільних сталих.
Якщо y1 і y2 |
|
є незалежні частинні рішення рівняння y′′ + py′ + qy = 0 , то |
||||||||||||
рівняння |
|
y′′ + py′ + qy = f ( x) |
за |
методом |
|
|
Лагранжа знаходиться у вигляді |
|||||||
y = A y1 + B y2 , де A і B – функції від x, які задовольняють систему рівнянь: |
||||||||||||||
A′y1 + B′y2 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|||
A′y′ + B′y′ = f (x). |
|
|
|
|
|
|
|
|
|
|||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Звідси A′ = − |
y |
2 |
f ( x) |
, B′ = |
y f (x) |
, а ω = |
|
y1 |
y2 |
|
. |
|||
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|||||||
|
|
ω |
ω |
|
|
y′ |
y′ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
Зразок виконання індивідуального завдання |
|
||||||||||||||||
І. Обчислити невизначений інтеграл: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
а) |
∫ x2 sin 3xdx . |
Для обчислення даного інтегралу скористаємось формулою |
|||||||||||||||||||||||
інтегрування |
частинами |
|
(див. |
теоретичний |
розділ). |
Знаходимо: |
|||||||||||||||||||
∫ x2 sin 3xdx = − |
1 |
|
∫ x2 d cos 3x = − |
1 |
(x2 cos 3x − ∫cos 3xdx2 ) = − |
1 |
x2 cos 3x + |
2 |
∫ x cos 3xdx = |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
3 |
|
|
3 |
3 |
|
|
|||||||||||
− |
1 |
x2 cos 3x + |
2 |
∫ xd sin 3x = − |
1 |
x2 cos 3x + |
2 |
x sin 3x − |
2 |
∫sin 3xdx = |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3 |
9 |
|
|
|
3 |
|
9 |
|
9 |
|
|
|
|
|
|
|
|||||||||
− |
1 |
x2 cos 3x + |
2 |
x sin 3x + |
2 |
cos 3x + C . |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
3 |
9 |
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
|||||
|
|
|
|
|
|
3x 5 |
+ 2x 4 + x 3 + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
б) |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx . Перетворимо підінтегральний вираз до вигляду, зручного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
2 |
+ 64 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
для інтегрування: |
3x 5 |
|
+ 2x 4 |
+ x 3 + 7 |
= 3x 3 |
+ 2x 2 − 191x − 128 + |
12224x + 8199 |
|
. Таким |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 + 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
+ 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
чином: |
|
∫ |
3x 5 + 2x 4 + x 3 + 7 |
|
|
= ∫(3x 3 + 2x 2 − 191x − 128 + |
|
12224x + 8199 |
|
|
|
Відзначимо, |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)dx . |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
2 |
+ 64 |
|
|
|
|
|
|
|
|
|
x |
2 |
+ 64 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
що d (x 2 + 64) = 2xdx , тоді: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
∫(3x |
3 |
+ 2x |
2 |
− 191x |
− 128 + |
12224x + 8199 |
)dx = |
3 |
|
x |
4 |
+ |
2 |
|
x |
3 |
− |
191 |
|
x |
2 |
|
− 128x + 6112∫ |
|
|
|
2xdx |
+ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
2 |
|
+ 64 |
|
|
|
|
4 |
|
|
|
3 |
|
|
|
2 |
|
|
|
x |
2 |
+ 64 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
+ 8199∫ |
|
|
|
dx |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
+ 64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
3 |
x 4 |
+ |
|
2 |
|
x |
3 |
− |
191 |
|
x 2 − 128x + |
|
6112∫ |
|
d ( x 2 |
+ 64) |
|
+ |
8199 |
arctg |
x |
= |
3 |
x 4 + |
2 |
x |
3 − |
191 |
x 2 |
− 128x + |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
3 |
|
|
|
|
2 |
|
|
|
x |
2 |
+ 64 |
|
|
|
|
8 |
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
+ 6122 ln(x 2 |
+ 64) + |
8199 |
arctg |
|
|
x |
+С. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
в) |
|
|
|
|
∫ |
|
|
|
|
|
x + 7 |
|
|
|
|
dx . |
Враховуючи, |
|
|
що |
|
|
|
|
d (x 2 |
|
+ 6x − 3) = (2x + 6)dx , |
|
|
|
перетворимо |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
+ 6x − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(2x + 6 − 6) + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
підінтегральний вираз: |
|
|
|
|
|
x + 7 |
|
|
|
|
|
2 |
|
1 |
|
|
|
|
2x + 6 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 + 6x − 3 |
|
|
|
|
|
|
|
|
|
|
|
x 2 + 6x − 3 |
|
|
|
|
|
|
|
|
|
|
x 2 + 6x − 3 |
|
|
|
|
|
|
|
( x + 3) 2 − 12 |
||||||||||||||||||||||||||||||||
Тепер |
|
|
даний |
|
|
|
|
інтеграл |
|
|
|
|
можемо |
записати |
|
|
|
у |
|
вигляді: |
|
|
∫ |
|
|
|
|
|
|
|
x + 7 |
|
|
dx |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
+ 6x − 3 |
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
2x + 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
1 |
|
|
|
d ( |
|
2 |
+ 6x − 3) |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
= |
|
|
∫ |
|
|
|
|
|
|
|
dx + ∫ |
|
|
|
|
|
dx = |
∫ |
x |
+ ∫ |
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
2 |
− 12 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
+ 6x − 3 |
|
|
|
|
|
|
|
|
|
|
( x + 3) |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
x |
|
+ 6x − 3 |
|
|
|
|
|
|
|
( x + 3) |
− 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Використовуючи таблицю інтегралів, остаточно знаходимо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x + 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
dx = x 2 + 6x − 3 + ln |
x + 3 + (x + 3) |
2 − 12 |
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
+ 6x − 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
г) |
|
∫sin 3 2x cos 2 2xdx . Для обчислення даного інтегралу виконаємо перетворення: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫sin 3 |
2x cos 2 |
2xdx = |
1 |
|
∫sin 3 2x cos 2 2x d 2x = |
1 |
∫sin 2 2x cos 2 2x sin 2xdx . З урахуванням |
||||||
|
|
||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|||
того, що d cos 2x = − sin 2xd 2x , знаходимо: |
|
|
|
||||||||||
∫sin 3 |
2x cos 2 |
2xdx = − |
1 |
∫sin 2 2x cos 2 2x d cos 2x = |
1 |
∫(cos 2 2x − 1) cos 2 2x d cos 2x = |
|||||||
|
|
||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|||||
= |
1 |
cos5 2x − |
1 |
cos3 2x + C . |
|
|
|
||||||
|
|
|
|
|
|||||||||
10 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|

50
II. Знайти визначені інтеграли:
16 |
16 |
а) ∫(
 4x + 3
4x + 3  x )dx . За формулою Ньютона-Лейбниця знаходимо: ∫(
x )dx . За формулою Ньютона-Лейбниця знаходимо: ∫(
 4x + 3
4x + 3  x )dx =
x )dx =
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
3 |
|
|
|
|
4 |
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x 2 |
|
|
|
x 3 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
3 |
|
|
|
|
256 |
|
|
|
|
|
|
|
|
64 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
16 |
2 + |
|
|
16 3 |
|
− |
|
|
|
8 2 + |
|
8 |
3 = |
|
|
|
|
+ 243 2 |
− |
|
|
|
|
− 12 |
= |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= |
|
220 |
+ 243 |
|
|
|
|
|
− |
64 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
б) ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
Зробимо |
|
|
заміну |
змінних |
у |
|
визначеному |
інтегралі: |
|
5x + 1 = t , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
|
3 + |
|
|
5x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
2 |
− 1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
dx |
|
|
|
|
||||||||||||
5x + 1 = t 2 , x = |
|
|
, dx = |
tdt . |
|
|
Після |
|
|
|
|
заміни |
|
|
|
|
|
змінних |
|
маємо: |
∫ |
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
3 + 5x + 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
21 |
|
2 |
|
|
|
|
tdt |
|
|
|
|
|
|
|
2 |
|
21 |
|
t + 3 − 3 |
|
|
|
|
2 |
|
21 |
|
|
|
|
3 |
|
|
|
|
|
2 |
21 |
|
|
21 |
d (t + 3) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
= ∫ |
|
|
|
|
|
|
= |
|
∫ |
|
dt = |
|
∫ (1 − |
|
|
)dt = |
|
∫ |
|
dt − 3 ∫ |
= |
(t − 3 ln(t + 3)) |
|
1 |
21 = |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t + 3 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
5 3 + t |
5 |
|
1 |
|
|
|
|
|
t + 3 |
|
|
5 |
|
1 |
|
|
|
|
|
t + 3 |
|
|
|
|
5 |
|
1 |
|
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
= |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3)) − (1 − 3 ln 4)) = |
2 |
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 + 3 |
)) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
(( 21 − 3 ln( |
|
|
21 |
|
|
21 − 1 − 3 ln( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
III. Зробити рисунок та знайти площу фігури, обмеженої даними кривими:
y = |
5 x 2 |
, y = 16 − |
3 |
x 2 . |
|
|
|||
2 |
2 |
|
||
Зробимо рисунок (Рис. 8.).
