
Matem_Lisitsya_2
.pdf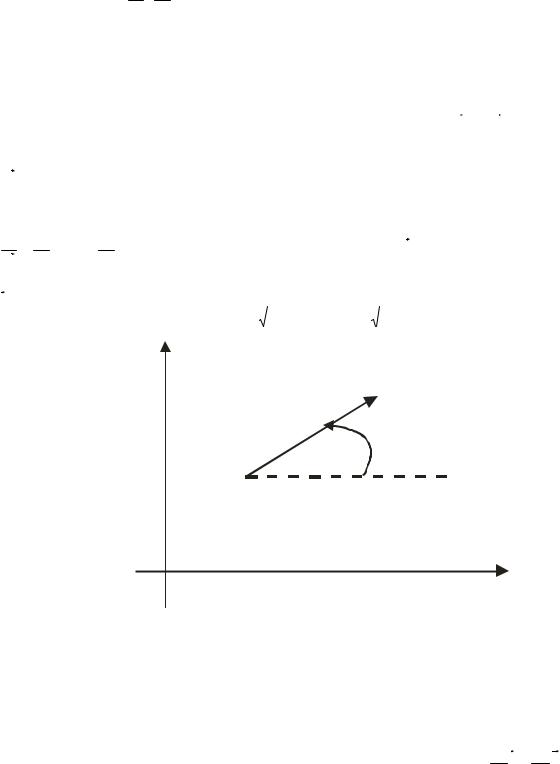
21
Частинна похідна по y від функції z = f (x, y) позначається одним з
символів: z y′, f y′, ∂z , ∂f .
∂y ∂y
|
|
|
|
Похідна у даному напрямку |
|
|
Похідною функції |
z = f (x, y) у даному напрямку l = PP |
називається |
||
|
|
|
|
1 |
|
∂z |
= lim |
f (P ) − f (P) |
, де f |
(P) та f (P ) – значення функції в точках P та P . |
|
|
1 |
||||
|
|
|
|
|
|
∂l |
PP →0 |
PP1 |
|
1 |
1 |
|
|
|
|||
|
1 |
|
|
|
|
|
Якщо функція |
z диференційована, то справедлива |
формула |
||
∂z = ∂z cosα + ∂z sin α , де α – кут, який утворює вектор l з віссю Ox. Якщо вектор
∂l ∂x |
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
l має координати (l1 ; l |
2 ) , то cosα = |
|
l1 |
|
, sin α = |
|
l2 |
(Рис.2). |
|||||
|
|
|
|
|
|
|
|
||||||
l 2 |
+ l 2 |
l 2 |
+ l 2 |
||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(x ; y ) |
|
|||||
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
||
α
P(x; y)
O X
Рис. 2
Градієнт функції
Градієнтом функції z = f (x, y) називається вектор grad z = ∂z i + ∂z j .
∂x ∂y

|
|
|
|
|
|
|
22 |
Похідна даної |
функції z = f (x, y) у даному напрямку l |
пов’язана |
з |
||||
градієнтом функції |
наступною формулою: |
∂z |
= grad z; l , |
де |
дужками |
; |
|
|
|||||||
|
|
∂l |
|
|
|
|
|
позначено скалярний добуток векторів. |
|
|
|
|
|||
|
Екстремум функції двох змінних |
|
|
|
|||
Функція z = f (x, y) має максимум (мінімум) |
у точці P(x0 , y0 ) , якщо для |
||||||
всіх відмінних від P(x0 , y0 ) точок P′(x, y) у достатньо малому околі точки |
P |
||||||
виконується нерівність f ( x0 , y0 ) > f ( x, y) (або відповідно, f ( x0 , |
y0 ) < f (x, y) ). |
|
|||||
Максимум або мінімум функції називається її екстремумом. |
|
||||||
Необхідні умови екстремуму. |
|
|
|
|
|||
Точки, в яких диференційована функція |
z = f (x, y) |
може досягати |
|||||
екстремуму (стаціонарні точки), знаходяться шляхом рішення системи
рівнянь: |
f x′(x, y) = 0 , |
f y′(x, y) = 0 (необхідні умови екстремуму). |
|
|||||||||||
|
Достатні умови екстремуму. |
|
|
|
|
|
||||||||
|
Нехай |
P(x0 , y0 ) − |
|
стаціонарна |
точка функції z = f (x, y) . |
Позначимо: |
||||||||
A = f ′′ |
( x |
, y |
0 |
) , |
B = f ′′ |
(x |
, y |
0 |
) , C = f ′′ |
(x |
, y |
0 |
) . Складемо дискримінант |
= AC − B 2 . |
xx |
0 |
|
|
xy |
0 |
|
yy |
0 |
|
|
|
|||
Тоді:
1)якщо > 0 , то функція z = f (x, y) має екстремум у точці P(x0 , y0 ) , а
саме максимум, якщо A < 0 (або C < 0 ), та мінімум, якщо A > 0 (або C > 0 );
2)якщо < 0 , то екстремуму в точці P(x0 , y0 ) немає;
3) якщо = 0 , то питання про наявність екстремуму функції у точці
P(x0 , y0 ) залишається відкритим (потрібно проводити подальші дослідження).
Поняття про емпірічні формули. Метод найменших квадратів
На практиці часто виникає задача про наближення експериментальних даних тією чи іншою диференційованою функцією. Наприклад, залежність між двома змінними x та y може виражатися у вигляді таблиці, отриманої шляхом спостережень, дослідів, статистичної обробки тощо:

23
x |
x1 |
x2 |
... |
xi |
... |
xn |
|
|
|
|
|
|
|
y |
y1 |
y2 |
… |
yi |
… |
yn |
|
|
|
|
|
|
|
Треба найкращим чином наблизити експериментальну залежність між змінними x та y, тобто якомога точніше відобразити загальну тенденцію залежності y від x. Часто такою залежністю виступає лінійна функція
Згідно з методом найменших квадратів лінійну функцію підбирають таким чином, щоб сума квадратів відхилень даних, знайдених під час експерименту, від теоретичної лінійної залежності була найменшою. Тобто,
|
|
|
n |
|
|
|
потрібно знайти мінімум виразу |
S = ∑(axi + b − yi ) 2 . Величини xi та |
yi |
– дані |
|||
|
|
|
i=1 |
|
|
|
експерименту. Таким чином, функція S |
залежить від двох змінних a |
та b , |
||||
тобто S = S(a;b) . Щоб знайти |
мінімум |
цієї функції, достатньо |
вирішити |
|||
систему: |
|
|
|
|
|
|
|
|
n |
|
|
|
|
Sa |
= 0, |
∑2(axi + b − yi )xi =0, |
|
|
|
|
|
= 0, |
або i =n1 |
|
|
|
|
Sb |
∑2(ax + b − yi ) = 0. |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
Після алгебраїчних перетворень ця система приймає вигляд:
|
n |
n |
n |
|
(∑xi2 )a + (∑xi )b = ∑xi yi , |
і називається системою нормальних рівнянь. |
|||
|
n |
i =1 |
n |
|
|
i =1 |
i =1 |
|
|
(∑xi )a + nb = ∑ yi |
|
|||
|
i =1 |
|
i =1 |
|
У математичній літературі доводиться, що отримана система має єдине рішення і знайдені рішення системи дають мінімум функції.

24
Зразок виконання індивідуального завдання
I. Знайти похідні даних функцій.
Для знаходження похідних функцій скористаємось таблицею похідних та правилами диференціювання.
а) y = |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x 5 − |
+ 25 x 3 |
− 6 . |
|
|
|
|
|
|
|
||||||
|
(3x) 2 |
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для знаходження похідної даної функції скористаємось табличною |
|||||||||||||||
формулою похідної (xα )′ = α xα −1 та правилом, |
за яким похідна суми функцій |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
дорівнює сумі |
похідних. |
Таким чином: |
|
1 |
|
1 |
|
|
|
||||||
y′ = ( |
x 5 )′ − ( |
x −2 )′ + (2x 5 )′ − (6)′ . |
|||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
3 |
9 |
|
|
|
|||
Враховуючі, що константу можна виносити за знак похідної та похідна від
константи |
|
дорівнює |
нулю, |
|
|
|
отримуємо |
остаточний |
результат: |
||||||||||||||||||
|
5 |
|
|
2 |
|
|
|
|
6 |
− |
2 |
|
5 |
|
2 |
|
|
6 |
|
|
|
|
|
|
|
||
y′ = |
x 4 + |
x −3 + |
x 5 = |
x 4 + |
+ |
|
|
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
9x 3 |
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
9 |
|
|
5 |
|
|
|
3 |
|
|
55 x 2 |
|
|
|
|
|
||||||||||
|
|
б) y = (4x 3 + 1) cos(x + 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Скористаємость |
|
правилом |
|
похідної |
добутку двох функцій. Тоді |
||||||||||||||||||||
y′ = (4x 3 + 1)′ cos(x + 1) + (4x 3 + 1)(cos(x + 1))′ =12x 2 cos(x + 1) − (4x 3 + 1) sin( x + 1) . |
|||||||||||||||||||||||||||
|
|
в) |
y = ln(2x5 + 3x) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
У даному прикладі скористаємось похідної складної функції, тобто, якщо |
|||||||||||||||||||||||||
y = f (ϕ (x)) , то y′ = f ′ ϕ ′(x)) . Таким чином: y′ = |
1 |
|
(2x 5 + 3x)′ = |
10x + 3 |
. |
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ϕ |
|
|
|
|
|
|
|
|
|
(2x 5 + 3x) |
2x 5 + 3x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
г) y = |
|
e 2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
3 |
x + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Похідна |
частки |
|
|
u(x) ′ |
u′(x) v(x) − u(x) v′(x) |
|
||||
|
|
|
= |
|
|
. |
|
|
|
||||
v(x) |
|
v 2 |
(x) |
|
||
функцій знаходиться за формулою:
Знаходимо похідну даної функції:
|
|
|
|
|
|
|
|
|
2e 2 x (3 |
|
+ 1) − |
1 |
e 2 x |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
y′ = |
(e 2 x )′ (3 |
x + 1) − e 2 x (3 x + 1)′ |
3 |
|
3 x 2 |
e 2 x (6(x + 3 x 2 ) − 1) |
. |
||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
(3 x + 1) 2 |
(3 x + 1) 2 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
33 x 2 (3 x + 1)2 |
|
||||||||||||||||||
25
II. Дослідити функції та побудувати їх графіки:
Побудуємо графік функції y = 2x 3 − 9x 2 + 12x за схемою дослідження,
наданою у теоретичній частині.
1. Область визначення даної функції – x R .
2. Перевіремо функцію на парність: y(− x) = −2x 3 − 9x 2 − 12x . Очевидно, що
y(− x) ≠ ± y(x) . Таким чином, функція має загальний вигляд.
3. Знайдемо точки екстремуму, інтервали зростання та спадання функції.
Для цього |
знаходимо |
y′ = 6x 2 − 18x + 12 . Критичними |
точками даної |
функції |
||||
будуть |
точки, в яких |
y′ = 6x 2 |
− 18x + 12 = 6( x − 1)(x − 2) = 0 . |
Знайдемо |
ці |
точки: |
||
x1 = 1, x2 |
= 2 . |
Тепер знаходимо |
інтервали зростання |
та |
спадання |
функції і |
||
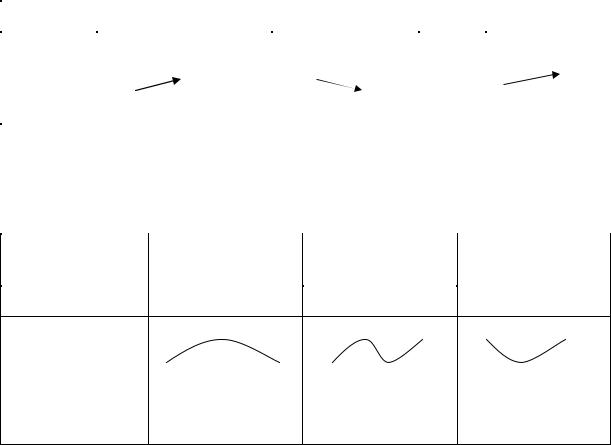
визначимо характер критичних точок:
інтервал |
|
]– ∞; 1[ |
1 |
|
]1 ; 2 [ |
|
|
2 |
|
] 2 ; ∞ [ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
+ |
|
0 |
|
– |
0 |
+ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
ymax |
= |
|
|
|
ymin = |
|
|
|
||
|
функція зростає |
= 5 |
|
функція спадає |
= 4 |
функція зростає |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Напрямок угнутості кривої знаходимо за допомогою другої похідної |
||||||||||||||
функції: y′′ = 12x − 18 = 12(x − |
3 |
) . |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
інтервал |
|
|
3 |
|
3 |
|
|
3 |
|
|||||
|
|
] –∞ ; |
|
|
[ |
|
|
|
|
] |
|
; ∞ [ |
||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
|
2 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|||||||
y′′ |
|
|
|
– |
0 |
|
+ |
|||||||
y |
функція опукла вгору |
точка перегину |
функція опукла вниз |
||||
|
|
|
|
|
|
|
|
|
|
y( |
3 |
) = |
9 |
|
|
|
|
|
|
|
|||
|
|
2 |
2 |
|
|
||
5. Знаходимо асимптоти кривої.
а) Вертикальних асимптот у даної кривої немає (див. теоретичну частину).
26
б) Для пошуку похилих асимптот знайдемо lim f ( x) = lim 2 x 3 − 9 x 2 + 12 x .
x→∞ x x→∞ x
Оскільки у даному випадку lim 2 x 3 − 9 x 2 + 12 x = ∞ , то похилих асимптот крива
|
|
x→∞ |
x |
також немає. |
|
|
|
6. Точки перетину функції з осями координат. |
|||
Точка перетину з віссю Oy : |
y(0) = 0 . Для того, щоб знайти точки перетину |
||
з віссю |
Ox , |
треба вирішити рівняння 2x 3 − 9x 2 + 12x = 0 . Перепишемо його у |
|
вигляді |
x(2x 2 |
− 9x + 12) = 0 . Рішеннями останнього рівняння є тільки x = 0 , тому |
|
що рівняння 2x 2 − 9x + 12 = 0 не має рішень.
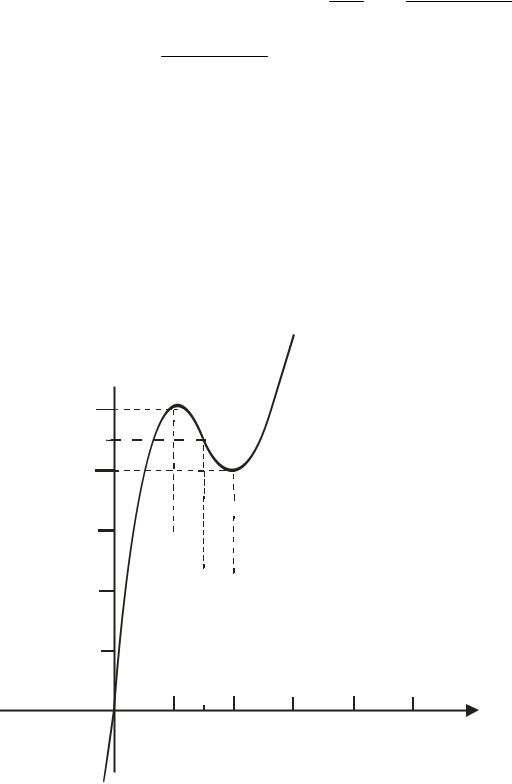
7. Використовуючи всі попередні дослідження, будуємо графік функції. (Рис.3).
Y  5
5
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
1 |
2 |
X |
||
Рис. 3.

27
Побудуємо графік функції y = |
x 2 − 1 |
. |
|
|
|
|
|
||||
|
|
|
|
||||||||
|
|
x + |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 |
|
|
|
|
|
|
|
|||
1. |
Область визначення даної функції: x ≠ − |
5 |
. |
|
|
|
|||||
|
|
|
|
||||||||
|
4 |
|
|
|
|
||||||
2. |
Перевіряємо функцію на парність: y(− x) = |
x 2 − 1 |
. Очевидно, що |
||||||||
− x + |
5 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
||
y(− x) ≠ ± y( x) , тобто функція має загальний вигляд.
|
2x ( x + |
5 |
) − (x 2 − 1) |
|
x 2 + |
5 |
x + 1 (x + |
1 |
) (x + 2) |
|
||||||||
|
|
|
|
|
|
|
||||||||||||
3. Знайдемо y′ = |
4 |
|
|
|
= |
2 |
|
|
= |
2 |
|
|
|
. Знаходимо |
||||
|
|
5 |
) 2 |
|
|
) 2 |
|
|
5 |
) 2 |
||||||||
|
(x + |
|
(x + |
5 |
|
(x + |
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
4 |
|
|
4 |
|
|
4 |
|
|
|||||||||
критичні точки даної функції та складемо таблицю для визначння інтервалів зростання та спадання функції і характеру критичних точок:
інтервал |
|
|
|
|
|
|
|
]−2; − |
5 |
[ |
|
|
|
− |
5 |
|
|
] − |
5 |
; − |
1 |
[ |
|
− |
1 |
|
|
|
] − |
1 |
; ∞[ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
]– ∞; –2[ |
−2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
4 |
|
|
2 |
|
2 |
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y ′ |
+ |
|
|
0 |
|
|
|
|
|
− |
|
|
|
|
|
|
∞ |
|
|
|
|
|
− |
|
|
|
0 |
|
|
|
+ |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y |
|
|
|
|
ymax = |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
ymin = |
|
|
|
|
|
|||||||
|
функція |
|
|
= − 4 |
|
функція |
|
функція |
|
функція |
|
= –1 |
|
|
функція |
||||||||||||||||||||||||||||
|
зростає |
|
|
|
|
|
|
|
спадає |
|
не існує |
|
спадає |
|
|
|
|
|
|
зростає |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
4. Напрямок угнутості кривої знаходимо за допомогою другої похідної |
|||||||||||||||||||||||||||||||||||||||||||
|
|
(2x + |
5 |
)( x + |
5 |
) 2 − 2( x + |
5 |
)(x 2 + |
5 |
x + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
функції: |
y′′ = |
|
2 |
|
4 |
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
= |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
( x + |
5 |
) 4 |
|
|
|
|
|
|
|
|
8(x + |
5 |
)3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
інтервал |
|
|
|
] –∞ |
; − |
5 |
|
[ |
|
|
|
|
|
|
|
|
− |
5 |
|
|
|
|
|
|
|
|
|
|
|
] − |
5 |
; ∞ [ |
|||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
y′′ |
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
+ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функція не існує |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y |
|
|
функція опукла вгору |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функція опукла вниз |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
5. Асимптоти кривої. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
а) Оскільки lim |
f ( x) = lim |
x 2 |
− 1 |
= −∞ , |
та |
lim |
|
f ( x) = |
|
lim |
x 2 − 1 |
= +∞ , |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
5 |
|
|
|
|
|
|
5 |
|
|
||||||||||||||||||||||||||||||||||||
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||
|
x→− |
|
−0 |
x→− |
|
−0 x + |
|
|
|
|
|
|
|
x→− |
|
|
+0 |
|
|
|
|
|
|
|
|
|
|
x→− |
|
+0 x + |
|
|
|
|
|
|||||||||||||
4 |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то вертикальною асимптотою даної кривої буде пряма x = − |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) Для пошуку похилих асимптот знайдемо |
k = lim |
|
|
f ( x) |
= lim |
|
x 2 |
|
− 1 |
|
= 1 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
5 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
x→∞ |
+ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( x |
|
|
|
) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
− |
5 |
x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Тепер знайдемо lim( f ( x) − kx) = lim( |
|
|
|
|
|
|
|
− x) = lim |
4 |
|
|
|
|
|
|
= − |
|
|
. Таким чином, |
|||||||||||||||||||||||||||||
|
|
5 |
|
|
|
|
|
|
|
5 |
|
|
|
4 |
||||||||||||||||||||||||||||||||||
|
x→∞ |
x→∞ |
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
|
x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
у даної кривої існує похила асимптота, рівняння якої y = x − |
5 |
|
|
(див. теоретичну |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
частину). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Точки перетину функції з осями координат. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Точка перетину |
з вісю Oy : y(0) = − |
4 |
. |
Точки |
перетину з віссю |
|
Ox : |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 − 1 = 0 . Рішеннями рівняння є точки x = −1 та x = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
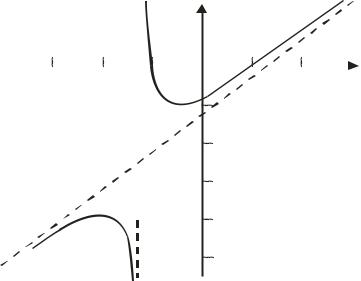
7. З урахуванням попередніх досліджень будуємо графік функції (Рис. 4). |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
-2 |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4
Рис. 4.
29
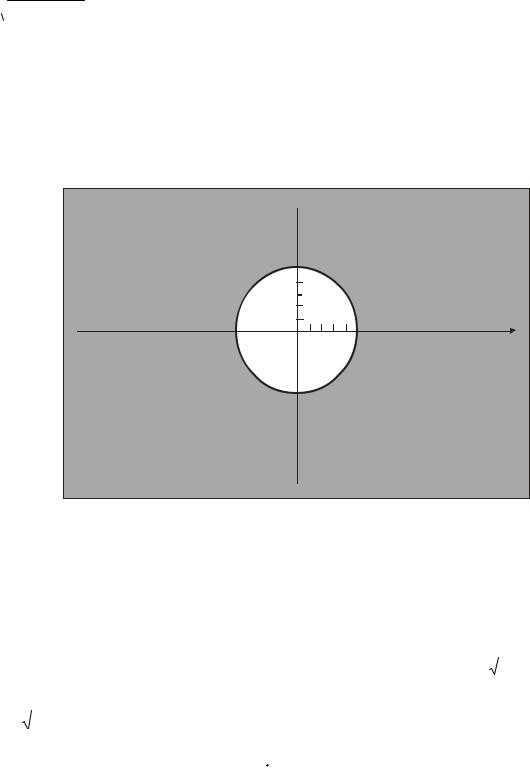
III. Знайти та зобразити на площині область визначення функції:
z = 
 x 2 + y 2 − 25 .
x 2 + y 2 − 25 .
Оскільки вираз під коренем другого ступеню повинен бути невід’ємним, то областю визначення даної функції будуть точки на площині, які задовольняють нерівності: x 2 + y 2 − 25 ≥ 0 . Ці точки лежать зовні кола радіуса 5 з
центром у точці О(0; 0). Коло теж входить в область визначення функції. Множина цих точок зображена на Рис. 5 (зафарбовано сірим фоном).
Y
5
O |
5 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IV. Задана функція |
z = 3x 2 − xy + y 2 , |
точка A(−1; 3) |
та вектор |
|
(3; − 4) . Знайти |
|||||||||||||||||||||||||||||
a |
||||||||||||||||||||||||||||||||||
grad z |
|
в точці А та похідну функції z в цій точці за напрямом вектора |
|
. |
|
|
|
|
|
|||||||||||||||||||||||||
a |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Знаходимо |
gradz = ( |
∂z |
; |
∂z |
) = (6x − y; − x + 2 y) , |
cosα = |
3 |
|
|
= |
3 |
, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∂x ∂y |
|
|
|
|
|
|
|
|
|
|
|
32 + 42 5 |
|
|||||||||
sin α = |
|
|
− 4 |
|
= − |
4 |
(див. |
теоретичну частину). У |
точці |
A(−1; 3) |
обчислимо |
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
32 + 42 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
gradz= (−9; 7) . |
|
Нарешті |
знаходимо |
|
∂z |
= (−9) |
3 |
+ 7 (− |
4 |
) = − 11 |
− |
|
похідна |
даної |
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂l |
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функції за напрямом вектора |
|
(3; − 4) |
|
у точці |
A(−1; 3) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
30
V. Дослідити на екстремум функцію двох змінних: z = x 3 + 3xy 2 − 15x − 12 y .
Знаходимо частинні похідні та складаємо систему рівнянь для пошуку критичних точок даної функції:
|
∂z |
= 3x |
2 |
+ 3 y |
2 |
− 15 = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x |
2 |
+ y |
2 |
− 5 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
або |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= 6xy − 12 = 0 |
|
|
|
|
|
|
|
xy − 2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вирішуючи |
|
|
систему, |
|
|
|
|
|
отримаємо |
|
|
|
|
стаціонарні |
|
|
|
|
|
|
|
точки: |
||||||||||||||||||||||
P (1; 2), |
P (2; 1), |
P (−1; − 2), |
P (−2; − 1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тепер знаходимо похідні другого порядку: |
|
∂ 2 z |
= 6x, |
|
∂ 2 z |
= 6 y, |
|
|
∂ 2 z |
= 6x . |
||||||||||||||||||||||||||||||||||
|
∂x 2 |
|
∂x∂y |
|
|
∂y 2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Для кожної критичної точки складаємо дискримінант |
|
= AC − B 2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1) Для |
|
точки |
|
|
|
|
∂ |
2 |
z |
|
|
|
|
|
|
∂ |
2 |
z |
|
|
|
|
|
|
|
∂ |
2 |
z |
|
|
||||||||||||||
|
P (1; 2) : |
A = |
|
|
= 6, |
B |
= |
|
|
|
= 12, |
C = |
|
|
|
= 6, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
∂x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
∂x∂y P |
|
|
|
|
|
|
|
|
P |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
= AC − B 2 |
= 36 − 144 < 0 . Це означає, що в точці P (1; 2) екстремума немає. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) Для |
|
точки |
|
|
|
|
∂ |
2 |
z |
|
|
|
|
|
|
∂ |
2 |
z |
|
|
|
|
|
|
∂ |
2 |
z |
|
|
|
||||||||||||||
|
P2 (2; 1) : |
A = |
|
|
|
= 12, |
B |
|
|
|
|
|
|
|
|
|
|
|
= 12, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
= |
|
|
|
|
|
= 6, C = |
|
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
∂x |
|
|
P |
|
|
|
|
∂x∂y P |
|
|
|
|
|
∂y |
|
|
P |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
= AC − B 2 |
= 144 − 36 > 0 , |
A = 12 > 0 . |
Це означає, |
що в точці |
|
P (2; 1) функція має |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
мінімум. Цей мінімум дорівнює значенню функції при x = 2, y = 1 : |
zmin |
|
= −28 . |
|||||||||||||||||||||||||||||||||||||||||
3) Для точки |
|
|
|
∂ |
2 |
z |
|
|
P (−1; − 2) |
: |
A = |
|
|
= −6, |
|||
|
|
2 |
||||||
|
3 |
|
|
∂x |
|
|
||
|
|
|
|
|
P 3 |
|
||
= AC − B 2 = 36 − 144 < 0 . Це означає, що в точці
|
∂ |
2 |
z |
|
|
|
∂ |
2 |
z |
|
|
B = |
|
|
= −12, |
C = |
|
|
= −6, |
||||
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
∂y |
|
|
||
|
∂x∂y P |
|
|
|
P |
|
|||||
|
|
|
|
3 |
|
|
|
|
|
3 |
|
P3 (−1; − 2) екстремума немає.
4) Для
|
∂ 2 z |
|
||
C = |
|
|
|
= −12, |
|
2 |
|||
|
∂y |
|
|
|
|
|
P |
|
|
|
|
|
4 |
|
точки |
P4 (−2; − 1) : |
= AC − B 2 |
= 144 − 36 > 0 , |
максимум, який дорівнює zmax = 28 .
|
∂ |
2 |
z |
|
|
|
|
∂ |
2 |
z |
|
|
A = |
|
|
= −12, |
B = |
|
|
= −6, |
|||||
|
|
2 |
|
|
|
|||||||
|
∂x |
|
|
|
|
|
|
|
|
|
||
|
|
P |
|
|
|
∂x∂y P |
|
|||||
|
|
|
|
4 |
|
|
|
|
|
|
4 |
|
A < 0 . |
В точці |
P4 (−2; − 1) функція має |
||||||||||
