matan_metod_1.1

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский Национальный Университет им. В. Н. Каразина

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

y 1 x 2 e x2 .

1536. x = acos2t;

y = acos3t, (a > 0).

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

1 Мб

Скачать

☆

1 / 31 2 3 > Следующая >>>

ОРИЕНТИРОВОЧНЫЙ ПЛАН ЗАНЯТИЙ

	Тема	Занятия
1.	Элементы элементарной математики	2
2.	Элементы мат. логики и теория множеств	1
3.	Теория пределов	6
4.	Непрерывность и дифференцируемость	4
5.	Применение дифференциального исчисления	5
6.Комплексные числа		3
7.	Неопределенные интегралы	6

Методические материалы содержат задачи для решения на практических занятиях и для домашних заданий.

Литература.

1.Д. Демидович. Сборник задач и упражнений по математическому анализу.

2.Волковысский, Лунц, Араманович. Сборник задач по теории функций комплексного переменного.

3.К. Кудрявцев. Задачи по математическому анализу. Ч.1

4.*. Задачи без определенного адреса.

Баллы для зачета набираются следующим образом:

1.	Посещение лекций	10 баллов			(н	–2 балла).
2.	Посещение практических занятий				5	баллов (н –1 балл).
3.	Участие в практических занятиях				15 баллов.
4.	Контрольные работы		15 баллов.
5.	Домашние задания	15 баллов.
6. Коллоквиум 15 баллов			(н	–10 ).
7.	Зачет 25 баллов.
		Всего 100 баллов.
Оценки по зачету:		0–49 FX (не зачет),
	50–59 E, 60–69 D,			70–79 C,		80–89 B, 90–100 A

После зачета количество набранных баллов умножается на 0,6 и получившееся количество баллов есть стартовым для сдачи экзамена. На экзамен выносится 40 баллов:

ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

План занятий А. Множества. Отношение включения и равенства. Операции над

множествами ( CA, A, A B, A B, A \ B, A B симм. разн.). Б. Некоторые свойства операций над множествами:

1) A B B A ; 2) A B C A B C ;

3)A B C A B A C ;

4)A B C B A A C ;

5) A B

B ;

6) A B

Задачи для решения 1*, 2*, 3*, 4*

1*. Доказать тождества:

2) A \ A \ B A B ;

1) A \ B C A \ B A \ C ;

3) A \ B \ C A \ B A C ;

4) A \ B \ C A \ B C ;

5) A B C A B A C ;

6) A B A B A B .

2*. Доказать, что:

1) A B C A

C ;

2) A B C A

C ;

3) A \ B B A B A ;

4) A B C A B C C A ;

5) A B A C B C ;

6) A B A B A B .

3*. Для множеств X и Y определить тип включения

X Y, Y X , X Y :

а) X A B \ C ,

Y A B \ A C ;

б) X A B \ C,

Y A \ C B \ C ;

в) X A \ B C ,

Y A \ B A \ C .

4*. Доказать, что:

1) A B B A B ;

2) A B A A B ;

3) A \ B \ C A \ B C C A ;

4) A \ A \ B A B ;

5) A \ B B \ A A B \ A B ;

6) A \ B \ C A \ B C ;

7) A \ B C A C \ B C ;

8) A \ B C A B C ;

9) A B \ C A B \ C ;

10) A C \ B A \ B C .

ТЕОРИЯ ПРЕДЕЛОВ

Задачи для решения. Демидович 389, 390, 391,401*, *, 407,412, 416, 418*, 419

389. Определить точную нижнюю и верхнюю грани функции f(x) = 1/(1 + x2) для х R.

Определить точную верхнюю и нижнюю грани функций:

390. f x	2x	, x 0, .	391. f x x	1	,	x 0, .
	x2			x
1

401*. На языке « – » доказать, что lim x2 9 . Указать правило

x 3

нахождения по заданному .

*. Что обозначают следующие записи:

0 0

x a

f (x) b

0 0

x a

f (x) b

x a

f (x) b

0 0

x a

f (x) b

x a

f (x) b

0 0

x a

f (x)

407. Сформулировать с помощью неравенств:

а) y b 0,

x a ;

ж) y b 0,

x ;

в) y b 0,

x a 0 ;

з) y b 0,

x ;

д) y b 0,

x a 0 ;

и) y b 0,

x ;

*) y ,

x a 0 ;

*) y ,

x .

Найти пределы:

412. lim

1 x 1 2x 1 3x 1

416. lim

2x 3 20 3x 20 30

x 0

2x 1 50

x2 5x 6

x 1, x 2

x2 3x 2

418*. lim

x 5, x 3 .

419.

lim

x 1 x

Задачи для решения. Демидович 420, 424.1, 436,437, 440, 446, 448, 458, 469, 474, 475, 476,495, 499, 503, 505,507

420.

lim

x4 3x 2

424.1 lim

x100

2x 1

x 1 x5 4x 3

x 1 x50

2x 1

436.

lim

x 3 x 4 x

437. lim

1 2x 3

2x 1

x 4

8 3x x2 2

440.

lim

x 13 2 x 1

446.

lim

x 2 9

x 3

x 0

1 x 1 x

448.

lim

458.

lim

2x .

x 0 3

1 x 3 1 x

469. Найти постоянные а и b из условия:

lim

ax b

0 .

Найти пределы:

474.

lim

1 cos x

475.

lim

tgx sin x

x 0

sin 3 x

476.

lim

sin 5x sin 3x

495.

lim

sin x 3

x 0

sin x

1 2 cos x

x 3


499. lim	1 tgx		1 sin x	.
499. lim				.
x 0		x	3

505. lim sin x 1 sin x .

503. lim	1			cos	x			.

x 0	1	cos				x
			x 2				x2
507. lim							.

x			2x 1

Задачи для решения. Демидович 508, 523, 525,

532, 533,535, 544, 545.3, 561(а,б), 563, 571, 579

508. lim 1 x2 ctg2x .	523.	lim		sin x tgx .
x 0		x
		x	2

ex 2 1

			1	cos					1 x
525.	lim sin									.
525.	lim sin									.
	x		x						x
533.	lim	ln x2				x 1						.
533.	lim											.
	x ln x10 x 1
				1
544.	lim x e x							.
544.	lim x e x				x			.
	x 0
											3		x
							ln 1				3
561 (a, б).		lim												.
561 (a, б).		lim											x	.
		x									2		x
							ln 1				2

571. lim 1 x sin x 1 .

x 0

532.

lim

sin ln x 1 sin ln x .

535.

lim

ln 2 e3x

x ln 3 e2x

545.3

lim

sin 2 2x

x 1 ln cos 2x

562.

lim

ln 1 2

ln 1

579. lim

esin 2x esin x

thx

x 0

Задачи для решения. Демидович 1325, 1326, 1331, 1332, 1333, 1349, 1354, 1363.3, 1398, 1399, 1402, 1404

Найти пределы:
1325.	lim	x ex		1 2 e x 1					.
1325.	lim			x3					.
	x 0			x3
1331.	lim	ln sin ax			.
1331.	lim				.
	x 0 ln sin bx
1333.	lim	cos sin x cos x						.
1333.	lim							.
	x 0			x4
			1	1
1354.	lim						.
1354.	lim			e x			.
	x 0 x			e x		1

1326. lim 1 cos x2 .

x 0 x2 sin x2

ln cosax

1332. lim . x 0 ln cosbx

1349. lim ctgx sin x .

x 0

arctgx x2

1363.3. lim . x 0 x

		cos x e			x2									e x sin x x 1 x
		cos x e			2									e x sin x x 1 x
1398.	lim					.					1399.		lim					.
1398.	lim		x4			.					1399.		lim		x3			.
	x 0		x4										x 0		x3
									1										1
							x		1
			3		2						6					2
			3		2						6					2
1402.	lim	x		x				e x		x		1 .	1404.		lim x x		ln 1			.
1402.	lim	x		x				e x		x		1 .	1404.		lim x x		ln 1			.
	x					2									x				x

Задачи для решения. Демидович

646, 650, 651,652, 653,655

О-символика. Главный член.

646. Показать, что при х а:

а)

o o f x o f x

;

б)

O o f x o f x ;

в)

o O f x o f x ;

г) O O f x O f x ;

650. Пусть x 0. Доказать, что:

O x3 2 ;

а)

2x x2 O x ;

б)

xsin

;

0 ;

в)

x sin

г) ln x o

O 1 ;

д)

x x

~ 8 x ;

е)

arctg

651. Показать, что при х + :

1 O x

;

x 1

а)

б)

;

x2 1

O x

;

arctgx

в)

x x

sin x

г)

1 x2

652. Доказать, что при достаточно больших х > 0 имеют место неравенства:

а) x2 10x 100 0,001x3 ;

б) ln1000

; в) x10ex e2x .

653. Найти главный член при х 0:

а) 2x 3x3 x5 ;

б)

1 x 1 x ;

в) 1 2x 3 1 3x ;

г)

tgx sin x .

655. Найти главный член при х 1:

а) x3 3x 2 ;

б) 3 1 x ;

в) ln x ;

г) ex e ;

д) x x 1.

Задачи для решения. Демидович 656, 657,658, *, *, *. 656. Пусть x + . Найти главный член и определить порядок роста величин:

а) x2 100x 10000;

б)

2x5

;

в) 3 x2 x

;

г) 1 1 x .

657. Пусть x + . Найти главный член и определить порядок малости величин:

x 1

sin

а)

;

б)

x 1

x ;

в) x 2 2

x 1

x ;

г)

x4 1

658. Найти главный член при х 1:

1 x

ln x

а)

;

б)

;

в)

;

г)

;

д)

x2 1

1 x

sin x

1 x 2

1 x3

*. Определить главные члены простейшего вида для величин:

а)

ln x2

e x arcsin tg

x ;

x 2

б) e x 1

cos

x ;

x 3

x 1 ln 2 x x 0 ;

cos

в)

г)

arctgx3 sin 2x2 1 cos x x2 1 x 0 .

*. На языке « – » для х а

и для х записать утвержде-

ния в том, что функция у(х):

а) ограничена;

б) неограничена;

в) имеет предел;

г) бесконечно мала;

д) бесконечно большая;

е) отделена от нуля.

*. Записать определение множества:

а) ограниченного сверху;

б) ограниченного снизу;

в) ограниченного;

с) неограниченного сверху;

d) неограниченного снизу;

е) неограниченного.

*. Записать, что функция f(x) на множестве Х является:

а) ограниченной сверху:

б) ограниченной снизу;

в) ограниченной;

с) неограниченной сверху;

d) неограниченной снизу;

е) неограниченной.

*** Дополнение.

Формулы, связанные с замечательными пределами

(здесь везде x 0)

І. Замечательные пределы:

lim

sin x

lim

tgx

1 ;

lim

arcsin x

lim 1 x

e ;

lim

ln 1 x

lim

a x 1

ln a ;

lim

e x 1

lim

1 x 1

II. Замечательные эквивалентности:

sin x ~ x ;

tgx ~ x ;

arcsin x ~ x ;

1 x 1 x

~ e ;

ln 1 x ~ x ;

a x 1 ~ x ln a ;

ex 1 ~ x ;

1 x ~ 1 x .

ІІІ. Замечательные равенства:

sin x x o x ;

tgx x o x ;

arcsin x x o x ;

1 x

e o 1 ;

ln 1 x x o x ;

ex 1 x o x ;

a x 1 x ln a o x ;

1 x 1 x o x .

IV. Пять замечательных разложений функций в ряд Маклорена.

e x

1 x

...

;

n 0 n!

sin x x

... 1 n

2n 1

...

1 n

2n 1

1 !

2n 1 !

n 0

cos x 1

... 1 n

...

1 n

2n !

n 0

ln 1 x x

... 1 n 1

n 1

1 x 1 x 1 x 2

1 2 x3 ..

1 ... n 1

...

1 ... n 1

n 0

НЕПРЕРЫВНОСТЬ И ДИФФЕРЕНЦИРУЕМОСТЬ

Задачи для решения. Демидович 687, 689, 690, 692,702, 723, 762, 1*, 2*, 3*, 4*, 846, 850, 854, 871, 895,5*, 6* ,7* ,8* ,9*, 10*.

687. Определить характер точек разрыва функции y	x
		.
	1 x 2

Определить точки этих точек:


	y		x2 1
689.					.
		x3 3x 2

692.	y		1 cos x	.

			4 x2

разрыва функций и исследовать характер

			1	1
				x 1
690.	y	x				.

	1				1

			x 1		x
702.	у = х – [x].

723. y lim cos 2n x .

762. Показать, что уравнение ctgx = kx k R и x (0, ) имеет единственный непрерывный корень х = х(k).

Определить точки разрыва функций и исследовать характер этих точек:

1*.

1 x

2*.

. 3*. y

. 4*. y sgn x2 2x .

1 2x

x2 1

cos x

Найти производные следующих функций:

846.

x x2

850.

x2 1 x 3

x x2

1 x

y tg

ctg

854.

y x

1 x2 .

871.

y ln x

895.

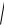5*. y x x x .

7*. y ex x2 2x 2 .

9*. y sin sin sin x .

12*. y x2 x 1 x2 x 1 .

6*. y e x2 .

8*. y e x eex .
10*. y ln ln ln x .	11*. y sin x cosx .

13*. y sin cos 2 tg3 x .

	2.
Задачи для решения. Демидович 979, 984,985,
986,999, 1004,1036, 1040, 1041, 1044, 1048, 1054.
979. Найти у и построить графики у(х) и у(х), если:
1 x	x 1
	x 1 x 2 .
y 1 x 2	x 1 x 2 .
x 2	x 2

984. Производная от логарифма данной функции y = f(x) называ-
ется логарифмической производной этой функции:
	y	d	ln	f x	f x	.


	y	dx			f x

Найти логарифмическую производную, если:

а)

y x

1 x

;

б)

x 2

1 x

в)

y x a1

x an

;

г)

x a2

y x

	3 x		;

	3 x 2
		n .
1 x 2

Найти у х если:							x
						y arctg		.
985.	а)	y	2 x 2 x	;	б)

							x
986.	а)	y f x 2 ;			б)	y f sin2 x f cos 2 x ;
	в)	y f e x e f x ;			г) y f f f x .
999. Исследовать на дифференцируемость:
	а) y = (x – 1)(х – 2)2(х – 3)3 ;					б) y = cosx ;
	в) y = 2 – х2 sin2x;					г) y = arcsin(cosx).

11
1004. Для f(x) определить левую f –(x) и правую					f +(x) произ-
		x
водную, если			x 0	.
		e1 x	x 0
	f x 1	e1 x
		0	x 0

1036. Определить область существования обратных функций

х = х(у) и найти	х у	если:	в) y = x + ex;
а) y = x + lnx;		б) y = shx;	в) y = x + ex;	г) y = thx.

Найти формулу для вычисления х' уy .

Найти у х, если:

1040.	x sin 2		t	.		1041. x a cos t, y b sint .

	y cos 2		t
1044.	x a t sin t				.	1048. х2 + 2ху – у2 = 2х.
		cos t
	y a 1

1054. Найти у х, если:

а) = а (спираль Архимеда); б) = а(1 + cos) (кардиоида); в) = аеm (логарифмич. спираль); , – полярные координаты.

Задачи для решения. Демидович 1087, 1088, 1090, 1092, 1093,1094, 1096, *, 1100, 1102, 1103, 1105.

Найти dy, если:

x a

1087.

1088.

y ln

x 2 a2

x a

1090. Найти:

а) d(xe );

б) d(sinx – хcosx);

в)

;

x 3

ln x

г) d

;

д)

;

е)

;

Найти dy, если :

1092. y	u	.		1093.

	v 2
				d tgx
1096. Найти: г)							;
				d ctgx
*. Найти:			а)		d	x 3
					dx 3

y	1		.	1094.	y arctg	u	.

	u 2 v2					v
д)		d arcsinx		.

		d arccos x
2x 6 x 9 ;				б) x ln x x ex .

Заменяя приращение функции дифференциалом, приближенно вычислить:

		б) sin29.
1100. а) 0,98 ;		б) sin29.
1102. arctg1,05.	1103 lg11.
1105. Доказать приближенную формулу:
			x
	n an x a		x	(а > 0),

			nan 1
			nan 1

где х << a и с ее помощью вычислить:

а) 39 ; б) 480 ; в) 7100 ; г) 10 1000 .

Задачи для решения. Демидович 1125,1128, 1132,1133, 1141,1142, 1144, 1156, 1158,1159, 1161,1165, 1166, 1169, 1173, 1189, 1207, *.

Найти y

1125.

y = f(x2);

1128. y = f(lnx).

Найти d2y:

1132.

ln x

1133.

y = xx.

Найти y ,

, y :

x f t

x a t sin t

1144.

x a cos t

;

1142.

f t

1141.

y a 1 cost

y tf t

y a sin t

Найти производные указанного порядка:

1056. у = x(2x – 1)2(х + 3)3;

у(6),

у(7) – ?

(10)

(8)

1158.

– ? 1159. y

;

– ?

1 x

1161.

y x2e2x ;

y(20) – ?

1165.

y x2 sin 2x ; y(50) – ?

1166.

cos3x

;

у – ?

1169.

y = excosx; yIV – ?

3 1 3x

1173. Найти d10y,

если y = xcos2x.

(n)

Найти y

1189.

1207.

y = e sinx.

x 1 x

*. Найти d2f,

если

f = f(1 + x2), где x = sint.

ПРИМЕНЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО

ИСЧИСЛЕНИЯ

Задачи для решения. 1*, 2*, 3*,4*, 5*,

6*, 7*, 8*, 9*, 10*, 11*, 12*, 13.

Следующие функции разложить в ряд Тейлора

в окрестности точки х = х0:

1*. у = х2 + 3х – 3, х0 = 0;

2*. у = х2 + 3х – 3, х0 = 1;

3*. y e x2 x , x0 0 (до х5);

4*. y

, х0 = 1, (до (х – 1)3);

Следующие функции разложить в ряд Тейлора до указанных степеней:

5*.

y ln 1 sin x , х0 = 0, (до х5).

6*.

до х4;

ex 1

7*. tgx до х5;

8*. sin(sinx) до х3;

9*. lncosx до х6;

10*. xx – 1 до (х – 1)3;

11*.

1 x2 x до

12*. Найти погрешность формулы: e x

1 x

			1					1
а) для	x	0,		;	б) для	x	0,		.
а) для	x	0,		;	б) для	x	0,		.
			2					4

13*. Вычислить с указанной точностью:


а) e до 10–5;	б) e до 10–8;	в) 4 e до 10–5;

г) 4 e до 10–8;	д) cos1 до 10–5.

Задачи для решения. Демидович 1288, 1289, 1394, 1395, 1397, 1414, 1414, 1419, 1429, 1431, 1432, 1437,1438.

1288. Доказать теорему: Если

1)функции (x) и (x) n–кратно дифференцируемы;

2)(k)(x0) = (k)(x0), k = 0, 1, 2, … n –1;

3)(n)(x) > (n)(x), x > x0,

то имеет место неравенство: (x) > (x), x > x0. 1289. Доказать неравенства:

	x3			tgx x	x3		x
в) x		sin x x (x > 0);	г)			0		.

	6				3			2

1394. Оценить погрешность формул:

0,1 ;

г)

(х[0, 1]).

в)

tgx x

1 x

1395.

Для каких х справедлива, с точностью до 0,0001, прибли-

женная формула: cos x 1

1397. Вычислить: в) cos9

( = 10–5);

г)

( = 10–5).

1410.

При каком

подборе

коэффициентов

b величина

x – (a + bcosx)sinx будет бесконечно малой 5

го

порядка относи-

тельно х.

Исследовать на экстремум:

1414. у = 2 + х – х2.

1419. у = (х + 1)10е–х.

1429.

у = х3 – 6х2 + 9х – 4;

1431. у = х(х – 1)2(х – 2)3.

y x

у = хе–х.

1438. y

1432.

;

1437.

x ln x .

Задачи для решения. Демидович 1445, 1446, 1447, 1452, 1453, 1454, 1462, 1473, 1476, 1477, 1479.

Найти наибольшее и наименьшее значение функции на множестве:

1445. у = 2х, х[–1, 5];		1446.	f(x) = x2 – 4x + 6, x[–3, 10];
1447. у = х2 – 3х + 2 , х [–10, 10].
1452.	Найти sup и inf функции y		1 x2	, x 0, .
1452.	Найти sup и inf функции y			, x 0, .
			1 x4
1453. Найти наибольшее и наименьшее значения функции:
	f x e x2 cos x 2 , x R.
1454.	Найти верхнюю и нижнюю грань функции f					1	на
1454.	Найти верхнюю и нижнюю грань функции f					3 2	на
						3 2
интервале х +. Построить графики функций
	M x sup	f ;	m x inf		f .
	x			x
	x

1462. Определить число вещественных корней уравнения: х3 – 6х2 +9х – 10 = 0 и отделить эти корни.

Построить графики следующих функций:

		2			y		x
1473. у = (х + 1)(х –2) .				1476.					;
							1 x 1 x 2
	y	x 4			y	x2 x 1
1477.			.	1479.				;
		1 x 3				x 1 2

Задачи для решения. Демидович 1491,1497, 1498, 1507, 1509.1, 1531, 1534, 1536, 1541, 1547.

Построить графики следующих функций:

1491. y		x	.	1497. y = sinx + cos2x.


	3 x 2 1

1498. у = (7 + 2cosx)sinx.

1509. 1. у = е–2хsin2x.

			t 2
	x
	x			2
1534.		1	t	2	;
		1	t
			1
	y		1


			t	2
	1		t

1541. x3 + y3 – 3axy = 0.

1547. = аsin3 , (а > 0).

КОМПЛЕКСНЫЕ ЧИСЛА

Задачи для решения. Волковысский 1*, 1, 2*, 2, 3*, 3, 7, 8, 4*.

1*. Выполнить действия над комплексными числами в алгебраической форме: z1 = 2 + 3i; z2 = 2 – 3i; z3 = –2 + 6i. Найти:

z1 + z2; z1 – z2; 3z1 – 2z3;

z1 z3;

z1 z2;

;

; z 2

;

z3 .

1. Выполнить действия:

;

1 i

3 .

1 3i

2*. Представить в тригонометрической форме следующие ком-

плексные числа:1 + i; 2 – 2i; –1 – i; 1 3 i ; 3 i ; i; 3i; 5; 8 ; 3 –

4i; 3 + 4i.

2. Найти модули и аргументы чисел: 5) 2 + 5i; 6) – 2 + 5i.

3*. Используя тригонометрическую форму выполнить действия над комплексными числами: z1 = 1 + i, z2 1 3 i .

Найти	z1 z2;	z1	;	z2		;	z 40	;	z 66 .

		z2		z1			1		2

3. Решить уравнение:		z* = zn – 1			(n 2,		n N).

7. Исходя из геометрических рассмотрений, доказать неравенства:

z1 z2

;

z1 z2

Доказать эти же неравенства алгебраическим путем. Выяснить, когда имеет место знак равенства.

8. Исходя из геометрических рассмотрений, доказать:

2) z – 1

z – 1 + z arg z.

arg z

;

4*. Найти геометрические места точек удовлетворяющих следующим соотношениям:

1) Re(z + 2) > 1;

2) Re(z + 2) 1;

Im(z – 2 + i) > 1;

4) z 3;

5) 2 z – 2 + i < 4;

0 < argz /4;

7) 0 < arg(z – i) /4;

8) Rez + Imz = 1;

9) Re{z(1 + i)} = 2;

10)

0 < arg{z(1 – i)} /4;

11) Re

= 1;

12) z – 3 =

– 1 .

Задачи для решения. Волковысский 26,

28, 30, 32,

34, 35, 5*, 6*, 7*, 59, 60, 61.

Найти геометрические места точек:

26. z – z1 = z – z2 .

28.

0 < Re(iz) < 1.

30. z = Rez + 1.

32. Im

z z1

0; Re

z z1

0 .

z z2

34. 1). z < arg z, 0 arg z < 2 ; 2) z< argz, 0 < argz <2 .

35. 1) Re

2) Im

c , (cR).

5*. Найти значения корней и построить их:

4) 6 8 ; 5) 8 1 ; 6)

1 i ; 7)

3 4i ;

8) 3 2 2i .

6*. Вычислить значения корней из комплексных чисел:

1 i ;

i ;

1 ;

1 .

7*. Представить следующие комплексные числа в показательной форме: 1 + i; 1 3 i ; – 2 + 2i; 4i; 5; – 8.

59. Представить числа в показательной форме: 1; i; 1 i.

	i
60. Найти: e 2 , ek i		(k = 0, 1, 2, …).
61. Найти модули и главные значения аргументов чисел:
e2+i;	e2–3i;	e3+4i;	e–3–4i;	–aei (a > 0, \| \| );
e–i	(\| \| );	ei – ei (0 < 2 ).
			3.
		Задачи для решения. Волковысский
			8, 9, 10*, 62, 64, 68, 71, 74.

8*. Найти геометрическое место точек, удовлетворяющих со-

отношению

arg z 2 .

9*. Найти вещественную и мнимую часть чисел:

e2 3i ;

cos i;

sin i;

tg i.

1 i 1 i

i 1

10*. Вычислить: 2

;

; 3

;

3 i

;

i ;

;

62. Найти суммы: 1) 1 + cosx + cos2x + … + cosnx; 2) sinx + sin2x + … sinnx.

2	2	z = 1;
64. Доказать, что 1) sin	z + cos	z = 1;	2) sinz = cos		z .
				2

68. Найти действительные и мнимые части значений следую-

щих функций:

1) cos(2 + i);

2) sin2i;

3) tg(2 – i).

71. Вычислить: Ln4;

Ln(–1);

ln(–1);

Lni;

lni;

1 i

;

Ln(2 – 3i);

Ln(–2 + 3i).

74. Вычислить:

1 2 ;

2 ;

2i;

1–i;

ii;

1 i

1+i

;

(3 – 4i)

;

(– 3 + 4i)

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Задачи для решения. Демидович. 1628, 1635, 1636, 1640,1643, 1646,1648, 1649, 1656, 1658, 1659, 1662, 1663, 1665,1677, 1681, 1682, 1685.

Вычислить неопределенные интегралы:


1628.	3 x2 3dx .
		1


1636.	1		x x dx .

		x2

1643. x2 1 x2 1dx .

x4 1

1648. 1 sin 2x dx 0 x .

1656. 2x 3 10dx .

1659.		dx		.

	5x	2 5 2
	5x	2 5 2
1663.		dx	.


		3x2
	2	3x2

1635. 1 x 3 dx . x3 x

1640. x2 dx .

1 x2

1646.			e3x				1	dx .
1646.				e x			1	dx .
				e x			1
1649.	ctg2 xdx.
1658.						dx			.


					2		5x
1662.						dx		.

		2			3x2
		2			3x2
1665.	e x e 2x dx . .

1677.		xdx		.

	1	x2 2
	1	x2 2
1682.			dx	.


	x		x2 1
	x		x2 1

1681. sin 1 dx . x x2

1685.	x2 dx		.
	8x3	27 2 3

Задачи для решения. Демидович. 1709, 1715*, 1723, 1727, 1729, 1733, 1737, 1747, 1749, 1768, 1774, 1777, 1792, 1799, 1808, 1811, 1819.

1709.

arctgx

dx .

1715*.

17 2dx

1723.

dx .

1 x2

1 x19

1727.			x2dx		.		1729.		dx		.
1727.	1		x 100		.		1729.				.
	1		x 100					x 1		x 1
1737.				xdx		.	1747. sin 3 x dx .

		x		2 x 3
		x		2 x 3

1733. x 1 x 3 .

1749. sin 4 x dx .


1768.		x2dx				.		1774.	ln xdx	.	1777.	arct	g		x	dx	.
1768.						.		1774.		.	1777.						.
			2 x						x 1 ln x				x			1 x
1792.	xn ln xdx						n 1 .		1799. x2 sin 2x dx .
				1	x			1811. x5e x2 dx .
1808.	x ln			1	x		dx .				1819.			x2 a dx .
1808.	x ln				x		dx .				1819.			x2 a dx .
	1				x

Задачи для решения. Демидович. 1837, 1843, 1851, 1853, 1857, 1859, 1864, 1866, 1867, 1869, *, 1872, 1878, 1882, 1892, 1893.

1837.

1851.

xdx

5 x x2

1857.

x2 x 1

1864.

1 x x2

dx .

1 x x2

1867.

xdx

1 x 2 x 3

xdx

x 1 x 2 2

x2 x 1 .

1878.

x2 4x 4 x2 4x 5 .

1892.

x3 1 2

1843.					x5dx				.
1843.				x6 x3				2	.
				x6 x3				2
1853.						xdx							.



				1 3x2			2x4
1859.						dx						.


		x			1 x2
		x			1 x2			2
1866.					2x 3					dx .

		x			2 x 5
		x			2 x 5
1869.					x3 1						dx .
1869.	x3				5x2		6x				dx .
	x3				5x2		6x
1872.					x2 1						dx .
1872.	x 1 2 x 1										dx .
	x 1 2 x 1
1882.				xdx		.
1882.						.
		x3 1
1893.					dx		.

			x		2 1 3
			x		2 1 3

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.2015249 Кб5marketing (Автосохраненный).doc
#
01.07.2025172 Кб2Marketing is the management process for identif...docx
#
23.02.201563 Кб20MARKETING-2013.docx
#
11.11.2019918 Кб21Masenko_Mova_i_suspilstvo_2004.doc
#
23.02.20154 Мб14matan_belaev_1.1.pdf
#
23.02.20151 Мб24matan_metod_1.1.pdf
#
23.02.20151 Мб50matan_metod_2012_1.2.doc
#
01.03.2025644 Кб3matan.doc
#
13.03.2016624 Кб8Matem_Lisitsya_2.pdf
#
01.07.202587 Кб3Math 2012.doc
#
23.02.20151 Мб20MechanS2.doc