
0085730_32E51_mosin_v_g_matematicheskie_osnovy
.pdf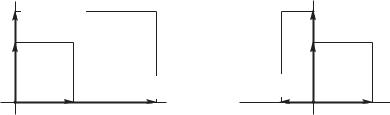
2.3. Линейные операторы |
|
|
|
61 |
|
стр. 60). Следовательно: |
откуда Matr E (Qx) = |
|
−1 |
. |
|
Qy (e2) = −e2 |
; |
0 |
|||
Qx(e1) = e1 |
, |
|
1 |
0 |
|
Аналогично получается утверждение для симметрии Qy относительно вертикальной оси (см. рис. 2.9, стр. 60).
Теорема 29 (матрица оператора масштабирования) В ортонормированном базисе e1, e2 матрица оператора Sk1,k2 масштабированния плоскости π с коэффициентами k1 по горизонтали и k2 по вертикали имеет вид:
Matr E (Sk1,k2 ) = |
0 |
k2 |
. |
|
k1 |
0 |
|
Доказательство Пусть на плоскости π фиксирован ортонормированный базис e1, e2.
Под действием оператора масштабирования Sk1,k2 единичный квадрат переходит в прямоугольник со сторонами k1, k2. При этом, так как вектор e1 лежит на горизонтальной оси, он просто растягивается в k1 раз, то есть — переходит в вектор k1 · e1 (см. рис. 2.10, стр. 61). Аналогично — вектор e2 переходит в вектор k2 · e2. Следовательно:
Sk1,k2 (e1) = k1 |
· |
e1 , |
откуда |
Matr E (Sk1,k2 ) = |
k1 |
0 |
. |
Sk1,k2 (e2) = k2 |
e2 ; |
0 |
k2 |
||||
|
· |
|
|
|
|
|
|
Sk1,k2 (e2) |
|
|
|
Sk1,k2 (e2) |
e2 |
|
|
|
e2 |
S |
k1 |
,k2 |
(e ) |
Sk1,k2 (e1) |
e1 |
1 |
e1 |
||
|
|
|
||
0 |
|
|
|
0 |
(a) Оба коэффициента масштабирова- |
(b) Коэффициент горизонтпльного |
|||
ния положительны. |
|
|
|
масштабирования отрицателен. |
Рис. 2.10: Действие операторов масштабирования на базисные векторы.
Пример 47 На плоскости π фиксирован ортонормированный базис e1, e2. Вычислить координаты вектора, в который перейдет вектор x = (1, 1) под действием оператора, сначала симметрично отражающего плоскость относительно горизонтальной оси, а затем — поворачивающего ее на угол π/4.
Интересующий нас оператор η — это произведение операторов Qx отражения относительно горизонтальной оси и Rπ/4 поворота на угол π/4:
η = Rπ/4Qx .
62 |
Глава 2. Линейная алгебра |
Отметим, что в силу некоммутативности алгебры линейных операторов (см. пример 41, стр. 53), произведение следует брать именно в этом порядке (справа налево: сначала на аргумент действует отражение, а уже потом — поворот).
Далее мы должны перевести оператор η в матричную форму. В силу теоремы о матрице произведения линейных операторов (см. теор. 24, стр. 57), матрица оператора η — это произведение двух матриц: матрицы оператора отражения и матрицы оператора поворота (произведение опять-таки берется в соответствующем порядке, а не иначе). Мы можем воспользоваться тем, что матрицы множителей нам известны (см. тер. 28, стр. 60 и теор. 27, стр. 59):
Matr E (η) = |
Matr E (Rπ/4)Matr E (Qx) = |
sin π/4 |
−cos π/4 |
|
0 |
−1 |
= |
||||||||||
|
|
|
|
|
|
|
cos π/4 |
sin π/4 |
|
|
|
1 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= |
1/√ |
2 |
−1/√ |
2 |
|
0 |
−1 = |
1/√2 |
−1/√ |
2 |
. |
|
|
||||
|
1/√2 |
1/√2 |
1 |
0 |
1/√2 |
1/√2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь — воспользуемся теоремой о действии линейного оператора на вектор в матричной форме (см. теор. 21, стр. 56) и получим ответ:
η(x) = |
1/√ |
2 |
−1/√ |
2 |
|
1 |
= |
2/0 |
2 |
. |
|
1/√2 |
1/√2 |
1 |
|
√ |
|||||
|
|
|
|
|
|
|
|
|
|
|
Глава 3
Проективные операторы
Выше мы убедились, что большинство преобразований плоскости реализуются в виде линейных операторов, которые, в свою очередь, могут быть описаны при помощи матриц при условии, что на плоскости фиксирован некий базис (см. теор. 27, стр. 59, теор. 28, стр. 60 и теор. 29, стр. 61). Следовательно, для хранения плоского преобразования в графической системе ей достаточно передать двумерный массив чисел длины 2. Кроме того, действие плоского преобразования, являющегося линейным оператором, сводится к матричному умножению (см. теор. 21, стр. 56), которое не требует от графической системы ничего, кроме сложения и умножения чисел. Процессор современного компьютера обладает очень высоким быстродействием, и выполнение таких операций с огромной скоростью позволяет выполнять линейные преобразования графической сцены в режиме реального времени.
 z
z
R3
y
P 2
x
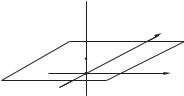
Рис. 3.1: Проективная плоскость P 2, вложенная в объемлющее трехмерное пространство R3.
ме.
Все это вселяет в нас сдержанный оптимизм.
Однако такое важное преобразование плоскости, как ее сдвиг (с точки зрения компьютерной графики оно означает смещение объекта относительно камеры или наоборот: смещение камеры относительно графической сцены), не является линенйным оператором (см. пример 33, стр. 48) и, следовательно, не может быть представлено в матричной фор-
В настоящей главе мы преодолеем это препятствие путем перехода от векторных пространств к проективным, в частности — от плоскости, как двумерного векторного пространства, к плоскости, как к двумерному проективному пространству (см. раздел 3.1, стр. 64).
Практичекские упражнения, относящиеся к данной теме, представлены в приложениях (см. приложение B.3, стр. 198). Кроме того, как основной
63

64 |
Глава 3. Проективные операторы |
практический результат первой части книги, мы подробно рассматриваем один из алгоритмов покадровой 2d-анимации с геометрической и аналитической точек зрения (см. раздел 3.3, стр. 71).
3.1Проективная плоскость
С геометрической точки зрения проективная плоскость ничем не отличается от обычной. Другое дело, что плоскость, рассматриваемая с проективной точки зрения, позволяет аналитически раелизовать сразу две важнейшие идеи:
•во-первых мы сможем отличать точки плоскости от векторов плоскости (заметим, что в пределах линейной алгебры это одно и то же),
•и во-вторых мы сможем в единой матричной форме реализовать все линейные плоские преобразования плюс смещение.
Определение 31 (проективная плоскость) Пусть в трехмерном физическом пространстве R3 фиксирован ортонормированный базис e1, e2, e3. Более того, будем считать, что на этом базисе в R3 построена координатная система с осями Ox, Oy, Oz. Проведем в R3 плоскость, проходящую через точку (0, 0, 1) параллельно плоскости xOy. Именно эта плоскость1, которую мы будем обозначать P 2, называется проективной плоскостью.
Итак, проективная плоскость P 2 получается из обыкновенной плоскости π пустем вложения ее в объемлющее трехмерное векторное пространство. Рассуждая аналогично, мы можем вложить трехмерное физическое пространство R3 в объемлющее четырехмерное пространство и получить тем самым проективное физическое пространство и т. д. Такой способ постороения проективных пространств приводит к следующей теореме, которая настолько очевидна (это, по сути, перефразировка определения), что мы примем ее без формального доказательства.
Теорема 30 (проективные координаты) Каждая точка A проективной плоскости P 2 обладает координатами вида (α1, α2, 1), а каждый вектор v проективной плоскости P 2 обладает координатами вида (β1, β2, 0). Такие координаты называются проективными координатами соответственно точки и вектора.
Таким образом, каждая точка проективной плоскости обладает одной “лишней” координатой: последнее, третье место всегда занимает 1, и каждый вектор проективной плоскости также обладает одной “лишней” координатой: третье место всегда занимает 0.
Это утверждение, очевидно, остается справедливым и для проективных пространств любой размерности: любая проективная точка в качестве своей последней координаты имеет 1, и каждый проективный вектор в качестве последней координаты имеет 0.
1Строго говоря, данное нами определение является лишь одной из возможных реализаций проективной плоскости. Для решения задач, которые нас интересуют этого вполне достаточно.
3.2. Проективные операторы |
65 |
3.2Проективные операторы
Здесь мы предъявим способ реализации всевозможных преобразований проективной плоскости в виде матриц 3 × 3.
Ключевым результатом этого раздела является теорема о проективности полскопараллельного смещения (см. теор. 35, стр. 68). Совместно с матричной реализацией поворотов, симметрий и масштабировний полученной выше, этот результат даст метод аналитического описания любого преобразования плоскости.
Определение 32 (проективный оператор) Пусть P 2 — это проективная плоскость, вложенная в объемлющее трехмерное векторное пространство R3. Далее, пусть в объемлющем пространстве действует линейный оператор ϕ:
ϕ : R3 −→ R3 .
Он называется проективным оператором, действующим в проективной плоскости P 2, если под его действием проективная плоскость P 2 переходит в себя:
ϕ : P 2 −→ P 2 .
Пример 48 Пусть P 2 — проективная плоскость, вложенная в объемлющее трехмерное пространство R3. Далее, пусть в R3 фиксирован ортонормированный базис e1, e2, e3, на котором построена координатная система. Рассмотрим поворот Rα объемлющего пространства относительно оси Oz на угол α:
Rα : R3 −→ R3 .
Он, очевидно, является линейным оператором. При этом под его действием проективная плоскость P 2 переходит в себя:
Rα : P 2 −→ P 2 .
Таким образом, мы получаем проективный оператор, действующий в проективной плоскости P 2, поворотом относительно начала координат на угол α.
С другой стороны, если мы рассмотрим поворот объемлющего пространства R3 на угол α относительно любой другой прямой, например, относительно оси Ox, то под действием такого преобразования плоскость P 2 перейдет в какую-то другую плоскость, но не в себя. Следовательно, несмотря на то, что этот поворот тоже является линейным оператором, действующим в объемлющем пространстве, он не является проективным оператором, действующим в проективной плоскости P 2.
Определение 33 (матрица проективного оператора) Пусть на проективной плоскости P 2 действует проективный оператор ϕ:
ϕ : P 2 −→ P 2 .
Его матрицей называется матрица соответствующего линейного оператора, действующего в объемлющем векторном пространстве:
ϕ : R3 −→ R3 .
66 |
Глава 3. Проективные операторы |
Пример 49 Рассмотрим поворот Rα проективной плоскости P 2 на угол α относительно начала координат. В объемлющем пространстве R3 ему соответствует поворот на угол α относительно вертикальной координатной оси Oz. Матрицу этого оператора нетрудно выписать. Так как в объемлющем пространстве фиксирован ортонормированный базис e1, e2, e3, то:
Rα(e2) |
= |
|
sin α |
· e1 |
+ |
cos α |
· e2 |
+ |
0 |
· e3 |
|
|
Rα(e1) = |
|
cos α |
e1 |
+ |
sin α |
e2 |
+ |
0 |
e3 |
|
Rα(e3) |
= |
− |
0 |
· e1 |
+ |
0 |
· e2 |
+ |
|
· e3 |
|
|
|
|
|
|
· |
|
|
· |
|
|
|
Из этих разложений, пользуясь определением матрицы линейного оператора, получаем:
Matr E (Rα) = |
sin α |
−cos α |
0 |
. |
|
|
|
cos α |
sin α |
0 |
|
|
|
0 |
0 |
1 |
|
Рассмотренный пример является частным случаем общей ситуации, которую мы изложим в виде следующей теоремы.
Теорема 31 (о матрице проективного оператора) Пусть на плоскости
π фиксирован ортонормированный базис e1, e2, и пусть она вложена как проективная плоскость P 2 в объемлющее трехмерное пространство R3, в котором фиксирован ортонормированный базис e1, e2, e3. Пусть на плоскости π действует линейный оператор ϕ:
ϕ: π −→ π ,
ипусть его матрица, выписанная в базисе e1, e2 — это:
Matr E (ϕ) = |
a11 |
a12 |
. |
|
a21 |
a22 |
|||
|
|
Тогда матрица соответствующего проективного оператора ϕ, действующего на проективной плоскости
ϕ : P 2 −→ P 2 ,
имеет следующий блочно-диагональный вид:
Matr E (ϕ) = |
a21 |
a22 |
0 |
. |
|
|
|
a11 |
a12 |
0 |
|
|
0 |
0 |
1 |
||
Доказательство По определению проективного оператора (см. опр. 32, стр.65), линейный оператор, действующий в объемлющем пространстве, на первые два базисных вектора e1 и e2 действует так же, как и на плоскости π, а третий базисный вектор e3 переводит в себя.
Подействуем на базисные векторы e1, e2 плоскости π в матричной форме:
ϕ(e1) = |
a21 |
a22 |
0 |
= |
a21 |
= a11e1 + a21e2 , |
|
a11 |
a12 |
1 |
|
a11 |
|
ϕ(e2) = |
a21 |
a22 |
1 |
= |
a22 |
= a12e1 + a22e2 . |
|
a11 |
a12 |
0 |
|
a12 |
|
3.2. Проективные операторы |
67 |
Следовательно, продолжая действие оператора на объемлющее пространство, получим:
ϕ(e2) = a12e1 |
+ a22e2 |
+ 0 |
· e3 |
|||||||||
|
ϕ(e1) |
= |
a11e1 |
+ |
a21e2 |
+ |
0 |
e3 |
||||
ϕ(e3) |
= |
0 |
· |
e1 |
+ |
0 |
· |
e2 |
+ |
|
· e3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Применим определение матрицы линейного оператора, выписывая коэффициенты разложений по столбцам, и получим требуемое.
Теорема доказана.
Теперь, при помощи этой теоремы, мы можем накрыть очень широкий блок проективных операторов, пользуясь теми результатами, которые получили выше.
Теорема 32 (матрицы проективных поворотов) Матрицы проективных поворотов Rα проективной плоскости P 2 на угол α относительно начала координат имеют вид:
Matr E (Rα) = |
sin α |
−cos α |
0 |
. |
|
|
|
cos α |
sin α |
0 |
|
|
0 |
0 |
1 |
||
Теорема 33 (матрицы проективных симметрий) Матрицы проективных симметрий Qx и Qy проективной плоскости P 2 относительно осей Ox и Oy соответственно имеют вид:
Matr E (Qx) = |
|
0 |
1 |
0 |
|
, |
Matr E (Qy ) = |
−0 |
1 |
0 |
. |
|
|
|
1 |
0 |
0 |
|
|
|
|
1 |
0 |
0 |
|
|
0 |
−0 |
1 |
|
|
0 |
0 |
1 |
||||
Теорема 34 (матрицы проективных масштабирований) Матрицы проективных масштабирований Sk1,k2 проективной плоскости P 2 относительно начала координат с коэффициентом k1 по горизонтали и с коэффи-
циентом k2 по вертикали имеют вид: |
|
|
|
. |
Matr E (Sk1,k2 ) = |
0 |
k2 |
0 |
|
|
k1 |
0 |
0 |
|
0 |
0 |
1 |
Все эти утверждения напрямую получаются из только что доказанной теоремы (см. теор. 31, стр. 66) с учетом результатов, полученных ранее относительно матриц операторов поворота (см. теор. 27, стр. 59), симметрий (см. теор. 28, стр. 60) и масштабирования (см. теор. 29, стр. 61). Их доказательства мы опускаем (они тривиальны).
Пример 50 Треугольник с вершинами A(1, −1), B(2, 3), C(−2, 5) равномерно двукратно масштабируется относительно начала координат. Вычислить координаты результирующего треугольника A B C .
Перейдем к проективным координатам A = (1, −1, 1), B = (2, 3, 1), C = (−2, 5, 1) и воспользуемся матричным представлением проективного масштабирования:
A = S2,2(A) = |
0 |
2 |
0 |
−1 |
= |
−2 . |
|
2 |
0 |
0 |
1 |
|
2 |
|
0 |
0 |
1 |
1 |
1 |
|
68 |
Глава 3. Проективные операторы |
Аналогично — B = (4, 6, 1), C = (−4, 10, 1). Следовательно, возвращаясь к декартовым координатам, имеем: A (2, −2), B (4, 6), C (−4, 10).
Пример 51 Треугольник с вершинами A(2, 1), B(2, 3), C(4, 1) поворачивается на угол π/2 относительно начала координат. Вычислить координаты результирующего треугольника A B C .
Перейдем к проективным координатам A = (2, 1, 1), B = (2, 3, 1), C = (4, 1, 1) и воспользуемся матричным представлением проективного вращения:
A = Rπ/2(A) = |
1 |
0 |
0 |
1 |
= |
−2 . |
|
0 |
−1 |
0 |
2 |
|
1 |
|
0 |
0 |
1 1 |
1 |
||
Аналогично — B = (−3, 2, 1), C = (−1, 4, 1). Следовательно, возвращаясь к декартовым координатам, имеем: A (−1, 2), B (−3, 2), C (−1, 4).
Пример 52 Треугольник с вершинами A(2, 2), B(3, 4), C(3, 2) симметрично отражается относительно вертикальной оси Oy. Вычислить координаты результирующего треугольника A B C .
Перейдем к проективным координатам A = (2, 2, 1), B = (3, 4, 1), C = (3, 2, 1) и воспользуемся матричным представлением проективной симметрии:
A = Qy (A) = |
0 |
1 |
0 |
2 |
= |
−2 . |
|
−1 |
0 |
0 |
2 |
|
2 |
|
0 |
0 |
1 1 |
1 |
||
Аналогично — B = (−3, 4, 1), C = (−3, 2, 1). Следовательно, возвращаясь к декартовым координатам, имеем: A (−2, 2), B (−3, 4), C (−3, 2).
Однако полученные матричные выражения для основных линейных преобразований плоскости не привнесли ничего нового в уже имевшийся у нас инструментарий работы с плоскостью. Те же самые действия мы могли бы выполнять и в декартовых координатах. Принципиально новым же является тот факт, что смещение плоскости мы можем реализовать в виде проективного оператора и, следовательно, в виде матрицы 3 × 3. Этот результат дает нам следующая теорема.
Теорема 35 (проективность смещения) Пусть преобразование Ta действует на плоскости π смещением на вектор a = (a1, a2) (предполагается, что на плоскости фиксирован ортонормированный базис e1, e2). Тогда Ta является проективным оператором, действующим на проективной плоскости P 2, причем он обладает следующей матрицей:
Matr E (Ta) = |
0 |
1 |
a2 |
. |
|
1 |
0 |
a1 |
|
0 |
0 |
1 |
Доказательство
Рассмотрим в объемлющем пространстве R3 преобразование Swa скоса на вектор a, действующее на базисные векторы следующим образом:
Swa(e1) = e1, |
Swa(e2) = e2, |
Swa(e3) = e3 + a .

3.2. Проективные операторы |
69 |
Отметим некоторые свойства этого преобразования.
Во-первых, оно, со всей очевидностью, является линейным. Во-вторых, оно переводит проективную плоскость P 2 в себя, причем в пределах P 2 скос объемлющего пространства действует именно как смещение на вектор a.
R3 |
|
z |
|
|
|
|
|
y |
|
|
a |
P |
2 e3 |
Swa(e3) |
|
|
|
|
|
x |
Рис. 3.2: Скос, действующий в P 2 как смещение.
оператором.
Действительно, так как вектор a лежит в горизонтальной координатной плоскости, прибавление его к любому вектору из R3 не изменяет его третьей координаты. В частности, любой вектор, лежащий в P 2, остается в ее пределах.
Следовательно, согласно определению (см. опр. 32, стр. 65), смещение Ta проективной плоскости P 2 на вектор a является проективным
Далее, мы можем выписать матрицу скоса:
Swa(e2) = 0 |
· e1 |
+ 1 |
· e2 |
+ 0 |
· e3 |
, |
||||||||
|
Swa(e1) |
= |
1 |
|
e1 |
+ |
0 |
|
e2 |
+ |
0 |
|
e3 |
, |
Swa(e3) |
= |
a1 |
· |
e1 |
+ |
a2 |
· |
e2 |
+ |
1 |
· |
e3 . |
||
|
|
|
|
· |
|
|
|
· |
|
|
|
· |
|
|
Выписывая коэффициенты разложений по столбцам, получим требуемое:
Matr E (Ta) = |
0 |
1 |
a2 |
. |
|
1 |
0 |
a1 |
|
0 |
0 |
1 |
Теорема доказана.
Теперь спектр наших возможностей преобразовать плоскость существенно пополнился, можно сказать, что теперь он стал окончательным: помимо прямых смещений плоскости, мы можем теперь выполнять масштабирования и повороты относительно произвольной точки плоскости, а также — симметрии относительно произвольных прямых. Проиллюстрируем это на примерах.
Пример 53 Треугольник с вершинами A(2, 1), B(2, 2), C(4, 2) вращается относительно точки G(1, 3) на угол π/2 (см. рис. 3.3, стр. 70). Найти координаты вершин результирующего треугольника A B C .
Поворот плоскости как линейный оператор возможен только относительно начала координат. Поэтому, для того, чтобы получить нужное нам преобразование η в матричной форме, необходимо сначала сместить центр вращения G(1, 3) на вектор b = (−1, −3) (то есть — выполнить трансляцию Tb), затем произвести поворот плоскости Rπ/2 на угол π/2 и после этого выполнить обратное смещение:
70 |
|
Глава 3. |
Проективные операторы |
|
y |
|
|
|
y |
|
π/2 |
|
|
|
G |
|
|
|
|
|
|
|
|
l |
0 |
x |
|
0 |
x |
(a) Поворот относительно произ- |
(b) Симметрия относительно про- |
|||
вольной точки. |
|
извольной (горизонтальной) оси. |
||
Рис. 3.3: Примеры линейных преобразования плоскости, использующих смещения.
трансляцию T−b на вектор −b = (1, 3).
η = T−bRπ/2Tb = |
|
0 |
1 |
3 |
|
sin π/2 |
|
cos π/2 |
0 |
|
0 |
1 |
−3 |
|
= |
||
|
|
1 |
0 |
1 |
|
|
cos π/2 |
− sin π/2 |
0 |
|
1 |
0 |
−1 |
|
|
||
|
0 |
0 |
1 |
|
0 |
|
0 |
1 0 |
0 |
1 |
|
||||||
= |
0 |
1 |
3 |
1 |
0 |
0 |
0 |
1 |
−3 |
= |
|
|
. |
||||
|
|
1 |
0 |
1 |
|
|
0 |
−1 |
0 |
1 |
0 |
−1 |
|
|
|
|
|
|
0 |
0 |
1 0 |
0 |
1 0 |
0 |
1 |
|
|
|
|
||||||
= |
|
1 |
−0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
00 1
Теперь можно вычислить координаты результирующего треугольника просто при помощи матричного умножения. Для этого — переходим к проективным координатам:
A = η (A) = |
1 |
−0 |
2 |
|
1 |
= |
4 |
|
таким образом |
A (3, 4). |
|
|
|
0 |
1 |
4 |
|
2 |
|
3 |
|
|
|
|
0 |
0 |
1 1 1 |
|
|
||||||
B = η (B) = |
1 |
−0 2 |
|
2 |
= |
4 |
|
и, значит, B (2, 4). |
|||
|
|
0 |
1 4 |
|
2 |
|
2 |
|
|
|
|
|
0 |
0 1 1 1 |
|
|
|||||||
|
|
0 |
1 |
4 |
|
4 |
= |
2 |
|
|
|
C = η (C) = |
1 |
−0 |
2 |
2 |
6 |
следовательно, |
C (2, 6). |
||||
|
|
0 |
0 |
1 |
|
1 |
|
1 |
|
|
|
Пример 54 Треугольник с вершинами A(2, 3), B(2, 5), C(4, 4) симметрично отражается относительно прямой l : y = 2 (см. рис. 3.3, стр. 70). Найти координаты вершин результирующего треугольника A B C .
Выше мы отнесли к основным плоским преобразованиям симметричные отражения Qx, Qy плоскости относительно координатных осей. Поэтому для реализации
