
0085730_32E51_mosin_v_g_matematicheskie_osnovy
.pdf
5.2. Производные |
131 |
5.2.5Производные высших порядков
В данном разделе мы рассмотрим вопросы последовательного дифференцирования функции и, тем самым, обобщим понятия непрерывности и гладкости функций понятием их бесконечной дифференцируемости (см. опр. 59, стр. 131)
Определение 58 (производные высших порядков) Допустим, функция f (x) дифференцируема на отрезке [a, b], то есть — на отрезке [a, b] определена функция f (x). Может оказаться так, точ функция f (x) снова будет дифференцируемой на [a, b]. В этом случае ее производная называется второй производной функции f (x):
f (x) = f (x) .
Аналогично определяются производные третьего и более высоких11 порядков:
f (x) = f (x) , и т. д. f (n) = f (n−1)(x) .
Пример 83 Будем последовательно дифференцировать многочлен:
f (x) = x3 + 2x , f (x) = 3x2 + 2 , f (x) = 6x , f (x) = 6 , f (x) = 0 .
Мы видим, что, начиная с производной четвертого порядка, все остальные производные оказываются равными нулю, то есть — существуют. Таким образом, мы можем заключить, что полиномальные функции являются бесконечно дифференцируемыми.
Пример 84 Будем последовательно дифференцировать логарифмическую функцию:
f (x) = ln x , f (x) = |
1 |
|
f |
1 |
|
f |
1 |
|
f |
1 |
|
||||
|
|
, |
(x) = − |
|
, |
(x) = 2 |
|
, |
(x) = 1 · 2 · 3 |
|
. |
||||
x |
x2 |
x3 |
x4 |
||||||||||||
Полученный ряд производных позволяет сделать вывод о существовании производной любого порядка от логарифмической функции, причем
f (n)(x) = (−1)n−1(n − 1)! x1n .
Таким образом, мы можем заключить, что логарифмические функции также являются бесконечно дифференцируемыми.
Определение 59 (класс C∞) О бесконечно дифференцируемых функциях говорят, что они образуют класс функций C∞.
Пример 85 Нетрудно убедиться, что ax, sin x, cos x C∞.
11Порядок производной заключается в скобки, чтобы отличать n-ю производную функции от ее n-й алгебраической степени.

132 |
Глава 5. Математический анализ |
5.2.6Производные функций, заданных параметрически
Определение 60 (производная параметрической функции) Пусть имеется функция, заданная параметрически при помощи параметра u:
p(u) = |
p1(u) |
; |
u [α1; α2] . |
p2(u) |
Пусть функции p1(u) и p2(u) являются дифференцируемыми на отрезке [α1; α2] как функции переменной u. Тогда производной параметрически заданной функции p(u) называется праметрически заданная функция p (u), определенная следующим образом12:
p1 |
(u) |
; u [α1; α2] |
p (u) = p2(u) |
||
Таким образом, дифференцирование функций, заданных параметрически, сводится в дифференцированию явных функций.
Пример 86 Вычислить производную функции, заданной параметрически:
sin 2u p(u) = .
u cos u
Согласно определению (см. опр. 60, стр. 132), нам достаточно по отдельности продифференцировать координаты функции p(u):
p1(u) = |
(sin 2u)) |
= 2 cos 2u , |
|
|
|||||||
p (u) = |
u cos u |
|
|
= u |
|
cos u + u |
|
(cos u) = |
|||
= |
|
· |
|
|
· |
− |
|
· |
− |
||
2 |
1 |
|
cos u + u ( |
· |
|
|
|
||||
|
|
|
|
sin u) = cos u u sin u . |
|||||||
Таким образом, производная данной параметрически заданной функции — это следующий вектор:
p (u) = |
2 cos 2u |
. |
|
cos u − u sin u |
|||
|
|
Пример 87 Вычислить значение производной функции p(u), заданной параметрически, при указанном значении параметра u:
3u
p(u) = |
|
1 |
+ u2 |
|
при u = 2 . |
3u2 |
|||||
|
|
|
|
|
|
|
|
1 |
+ u |
|
|
|
|
|
|
|
|
12В большинстве учебников принято другое определение производной функции, заданной параметрически. Такая функция связывает независимые переменные x и y опосредовано через параметр u, и обычно под производной такой функции понимают именно производную функции y по переменной x. Особенность нашего определения состоит в том, что мы дифференцируем функцию по параметру u, а не по одной из переменных.

5.3. Геометрический смысл производной |
133 |
Прежде всего, вычислим функцию, являющуюся производной функции p(u). Для этого (так же, как и выше) продифференцируем ее координаты.
p |
(u) = |
|
3u |
|
|
= |
(3u) |
· |
(1 + u2) − 3u · (1 + u2) |
= |
|
|||||||||
1 + u2 |
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
(1 + u2)2 |
|
|
|
|
|
|
||||||||
|
= |
|
3 · (1 + u2) − 3u · (0 + 2u) |
= 3 |
1 − u2 |
, |
|
|
|
|
||||||||||
|
|
|
|
|
(1 + u2)2 |
|
|
|
|
(1 + u2)2 |
|
|
|
|
|
|||||
p |
(u) = |
|
3u2 |
|
|
= |
(3u2) |
· |
(1 + u2) − 3u2 · (1 + u2) |
|
= |
|||||||||
1 + u2 |
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
(1 + u2)2 |
|
|
|
|
|
|||||||||
|
= |
|
6u · (1 + u2) − 3u2 · (0 + 2u) |
= 6 |
u |
|
. |
|
|
|
||||||||||
|
|
|
|
|
(1 + u2)2 |
|
|
|
|
|
|
(1 + u2)2 |
|
|
|
|
||||
Таким образом, производная функции p(u) — это следующая парметрически заданная функция:
|
|
3 |
|
1 − u2 |
|
|
|
p1(2) |
= − |
9 |
, |
||
|
(1 + u2)2 |
|
|
||||||||||
|
|
25 |
|||||||||||
|
|
|
|||||||||||
p (u) = |
|
6 |
|
u |
|
|
|
, при этом |
p |
(2) |
= |
12 |
. |
|
|
|
|
|
|
25 |
|||||||
|
|
|
|
|
|
||||||||
|
|
|
2 |
) |
2 |
|
|
2 |
|
|
|
||
|
|
|
(1 + u |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, искомое значение производной (при u = 2) — это вектор с числовыми координатами −9/25 и 12/25:
p (2) = (−9/25; 12/25) .
5.3Геометрический смысл производной
В этом разделе мы выясним геометрический смысл производной функции в точке (см. теор. 76, стр. 133) и, тем самым, получим инструмент для описания касательных к графикам явных функций (см. теор. 77, стр. 134). Несмотря на то, что в пиложениях нам понадобятся парметрические функции (см. главу 6, стр. 139), мы начинаем с явных функций: действия с парметрическими функциями во много повторяют действия с явными.
Практические задачи, относящиеся к этому разделу, представлены в приложениях (см. приложение C.2, стр. 213).
Определение 61 (касательная к кривой) Пусть M — точка, лежащая на непрерывной кривой C. Пусть M M — секущая к кривой C, проходящая через точки M и M . Касательной к кривой C, проведенной в точке M , называется предельное положение секущей M M , когда точка M бесконечно приближается по кривой C к точке M .
5.3.1Геометрический смысл производной явной функции
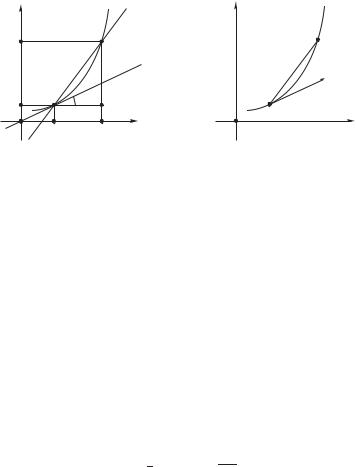
Теорема 76 (геометрический смысл производной) Пусть явная функция y = f (x) обладает производной f (x0) в точке x0. Тогда ее график
134 |
|
|
|
Глава 5. Математический анализ |
|
|
y |
|
|
y |
|
|
y0 + ∆y |
|
M |
|
p(u0 + ∆u) |
|
|
|
|
||
y0 |
M |
ϕ |
N |
p(u0) |
p (u0) |
|
|
|
|||
|
|
|
|
||
0 |
x0 |
x0 + ∆xx |
0 |
x |
|
(a) Явная функция. |
|
(b) Параметрическая функция. |
|||
Рис. 5.3: Геометрический смысл производной.
обладает касательной в точке (x0, f (x0)), причем
tg ϕ = f (x0) ,
где ϕ — угол наклона касательной к положительному направлению горизонтальной оси.
Доказательство Возьмем на графике функции точку M (x0, f (x0)). Пусть переменная x получает в точке x0 приращение ∆x. Возьмем на графике еще одну точку M (x0 + ∆x, y0 + ∆y) и проведем секущую M M .
Теперь мы можем рассмотреть прямоугольный треугольник M N M с катетами M N = ∆x и M N = ∆y (cм. рис. 5.3, стр. 134). Тангенс угла наклона секущей M M вычисляется, исходя из тригонометрических из соотношений в треугольнике M N M (как отношение длины противолежащего катета к
длине прилежащего):
∆∆xy .
Пусть теперь точка M стремится вдоль кривой к точке M . Тогда, очевидно, ∆x → 0 и секущая стремится к своему предельному положению, то есть — к касательной. Отсюда, пользуясь определениями (см. опр. 53, 61, стр. 117, 133), получим:
tg ϕ = f (x0) .
Теорема доказана.
Пример 88 Найдем тангенсы углов наклона касательной к кривой y = x2в точках M1(1/2, 1/4) и M2(−1, 1). Производная функции вычисляется элементарно:
y = 2x .
Поэтому (см. теор. 76, стр. 133):
tg ϕ1 = y (1/2) = 1 , |
tg ϕ2 = y (−1) = −2 . |
Теорема 77 (уравнение касательной) Пусть явная функция f (x) обладает производной в точке x0. Тогда ее график обладает касательной l в
точке x0, причем:
l : y = f (x0) + f (x0)(x − x0) .
5.3. Геометрический смысл производной |
135 |
Доказательство Пусть касательная l к графику функции y = f (x) имеет уравнение
l : y = kx + b .
Тогда, в силу теоремы о геометрическом смысле производной (см. теор. 76, стр. 133), имеем k = f (x0). Поэтому
l : y = f (x0)x + b .
Кроме того, известно, что прямая l проходит через точку (x0, f (x0)). Следовательно,
f (x0) = f (x0)x0 + b , откуда b = f (x0) − f (x0)x0 .
Используя найденные значения для k и b, окончательно получим:
l : y = f (x0)x + f (x0) −f (x0)x0 , то есть l : y = f (x0) + f (x0)(x −x0) .
Теорема доказана.
Пример 89 Запишем уравнения касательных к графику функции y = sin x в точках x1 = π/2 и x2 = π. Для этого нам необходимо знать значения функции в точках и значения ее производной:
y(π/2) = sin(π/2) = 1 ,
y (π/2) = cos π/2 = 0 ,
Поэтому (см. теор. 77, стр. 134):
l1 : y = 1 , l2
y(π) = sin(π) = 0 ,
y (π) = cos(π) = −1 .
: y = π − x .
5.3.2Геометрический смысл производной функции, заданной параметрически
Теорема 78 (геометрический смысл производной) Пусть кривая p(u)
описывается параметрически:
p(u) = |
p1 |
(u) |
. |
|
p2 |
(u) |
|||
|
|
Тогда вектор производной этой функции, вычисленный при значении пара-
метра u = u0,
p (u0) = p1(u0) p2(u0)
— это в точности вектор, касательный к кривой p(u), проведенный к ней в точке p(u0).
Доказательство Зафиксируем значение параметра u = u0 и придадим ему приращение ∆u (см. рис. 5.3, стр. 134). Тогда точка кривой M = p(u0) перейдет в точку M = p(u0 + ∆u). Координаты вектора M M таковы:
M M = |
p2 |
(u0 |
+ ∆u) |
− |
p2 |
(u0) |
= |
|
p1 |
(u0 |
+ ∆u) |
|
p1 |
(u0) |
|
=p1(u0 + ∆u) − p1(u0) p2(u0 + ∆u) − p2(u0)
∆p1
= . ∆p2

136 |
Глава 5. Математический анализ |
Это вектор, который является секущим вектором кривой p(u) в точке p(u0). Если точка M бесконечно приближается к точке M вдоль кривой, то вектор M M бесконечно приближается в касательному положению (см. опр. 61, стр. 133). Разделим вектор M M на ∆u и перейдем к пределу:
lim 1 ∆p1 |
|
|
|
∆p1 |
= |
∆u→0 |
∆p1 |
= |
|
|||
|
= lim |
∆u |
∆u |
p1(u0) . |
||||||||
∆u→0 |
|
∆p2 |
|
|
|
|
|
|
lim |
|
|
p2(u0) |
∆u |
∆u→0 |
∆p1 |
lim |
∆p1 |
||||||||
|
∆u |
∆u |
||||||||||
|
|
|
|
|
|
|
∆u 0 |
|
|
|||
|
|
|
|
|
|
|
|
|
→ |
|
|
|
Теорема доказана.
Пример 90 Вычислить касательный вектор к кривой
p(u) = |
u3 |
2u2 + 1 |
|
3u−2 + u − 4 |
|||
в точке, отвечающей значению параметра u0 = 2. Применим теорему о геометрическом смысле производной функции, заданной параметрически (см. теор. 78, стр. 135). Согласно ей, искомый касательный вектор — это p (2):
p (u) = |
3u2 − 4u |
, |
поэтому p (2) = |
3 |
22 − 4 · 2 |
= |
4 . |
|
6u + 1 |
|
|
|
·6 · 2 + 1 |
|
13 |
Аналогично тому, как мы выше описывали уравнения касательных к графикам явных функций, мы можем описать и касательные к параметрически заданным кривым при помощи их производных. Для этого нам понадобятся некоторые знания о том, как описываются прямые. Их явные уравнения вида y = kx+b — это не единственный способ их описать. Нам будет удобнее работать не с явными, а с каноническими уравнениями прямых.
Теорема 79 (каноническое уравнение прямой) Пусть прямая l проходит через точку A(xA, yA) параллельно вектору a = {a1, a2}. Тогда ее уравнение может быть записано в канонической форме следующим обра-
зом:
l : x − xA = y − yA . a1 a2
Доказательство Возьмем на прямой l переменную точку M с координатами (x, y). Тогда вектор AM с координатами {x − xA, y − yA}, лежащий на прямой l, по условию теоремы, должен быть параллелен вектору a. Параллельность же векторов означает пропорциональность их координат:
x − xA = y − yA . a1 a2
Теорема доказана.
Теорема 80 (уравнение касательной) Касательная к кривой p(u), описанной параметрически
p(u) = |
p1 |
(u) |
, |
|
p2 |
(u) |
|||
|
|
в точке, отвечающей значению параметра u = u0, имеет следующее каноническое уравнение:
x − p1(u0) |
= |
y − p2(u0) |
. |
p1(u0) |
|
||
|
p2(u0) |
||

5.3. Геометрический смысл производной |
137 |
Доказательство Воспользуемся двумя фактами. Во-первых, согласно теореме о геометрическом смысле производной функции, заданной параметрически (см. теор. 78, стр. 135), касательный вектор к кривой p(u) в точке, отвечающей значению параметра u = u0 — это вектор, составленный из производных (p1(u0), p2(u0)).
Во-вторых, касательная к кривой проходит через точку с координатами (p1(u0), p2(u0)). Поэтому, по теореме о каноническом уравнении прямой (см. теор. 101, стр. 215), получим:
x − p1(u0) |
= |
y − p2(u0) |
. |
p1(u0) |
|
||
|
p2(u0) |
||
Теорема доказана.
Пример 91 Записать уравнение касательной к кривой, описанной параметрически:
p(u) = |
2 cos u |
, |
|
5 sin u |
|||
|
|
в точке, отвечающей значению параметра u = π/4. Вычислим значение функции
при u = π/4: |
|
|
|
|
|
|
p(π/4) = |
5 sin π/4 |
= |
5√2/2 |
. |
||
|
2 cos π/4 |
|
√2 |
|
||
|
|
|
|
|
|
|
Далее вычислим значение производной при значении параметра u = π/4:
|
5 cos u |
|
|
5 cos π/4 |
|
|
√ |
|
|
|
||
5−√2/2 |
||||||||||||
p (u) = |
−2 sin u |
, |
поэтому p (π/4) = |
−2 sin π/4 |
|
= |
|
|
2 . |
|||
Теперь мы можем воспользоваться теоремой о касательной к кривой, описанной параметрически (см. теор. 80, стр. 136):
√√
l : |
x − |
2 = |
y − 5 2/2 . |
|||
|
√ |
|
|
√ |
|
|
|
− 2 |
|
5 2/2 |
|||
При помощи свойств пропорций из полученного канонического уравнения касательной можно вывести ее явное уравнение:
l : y = −52 x + 5√2 .
138 |
Глава 5. Математический анализ |

Глава 6
Интерполяция кривых
В качестве приложения математического анализа мы рассмотрим технику построения различных кривых по некоторым известным заранее их характеристикам1. Таким образом, в конце книги мы переходим к вопросам интерполяции кривых.
Имеются различные подходы к формированию криволинейной траектории, и, как следствие, различные типы интерполяций (см. опр. 37, стр. 93).
Если требуется, чтобы кривая проходила через набор заранее известных точек, то применяется прием точной интерполяции (см. раздел 6.1, стр. 139). Этот алгоритм используется во многих графических приложениях при формировании так называемых трехточечных кривых.
Если при построении кривой существенную роль играют направления, в которых кривая проходит через узловые точки, то используется интерполяция в форме Эрмита (см. раздел 6.2, стр. 143). Этот прием лежит в основе постороения так называемых кривых Безье.
При построении так называемых B-сплайнов, от формируемой кривой требуется, чтобы она проходила вблизи от опорных точек (точнее говоря, каждый ее сегмент должен лежать в пределах выпуклой оболочки последовательных четырех точек ее опорного ансамбля)2.
В этой главе мы теоретически обоснуем алгоритмы интерполяции и рссмотрим ряд примеров. Практические задачи, относящиеся к этой главе представлены в приложениях (см. приложение C.3, стр. 218).
6.1Точная интерполяция
Точная интерполяция (в отличие от кривых Безье или B-сплайнов) редко используется в графических системах. Однако принципы, которые используются при проведении точной интерполяции, позволяют понять механизм интерполяционных алгоритмов в общем случае.
1Еще раз отметим, что приложения математического анализа весьма обширны и вовсе не ограничиваются исследованием кривых.
2Этот прием мы не будем рассматривать, читатель может ознакомиться с ним в монографии Эдварда Энджела [E].
139
140 |
Глава 6. Интерполяция кривых |
Поэтому мы начинаем изучение интерполяционных алгоритмов с точной интерполяции.
y |
|
|
y |
y |
|
|
|
|
|
|
An |
C |
|
|
C |
A2 |
A3 |
B |
|
B |
D |
|
|
A |
|
A |
|
A1 |
|
0 |
x |
0 |
x |
0 |
x |
(a) Трехточечная |
точная |
(b) Четырехточечная точ- |
(c) n-точечная точная ин- |
||
интерполяция. |
|
ная интерполяция. |
терполяция. |
|
|
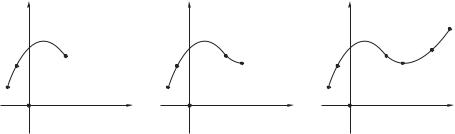
Рис. 6.1: Кривые, точно интерполирующие опорный ансамбль.
Определение 62 (точная интерполяция) Пусть на плоскости π фиксирован некоторый набор точек A1, . . . , An, который мы будем называть опорным ансамблем. Точной интерполирующей кривой для данного ансабля называется кривая C, проходящая через каждую точку ансамбля ровно по одному разу и в указанном порядке.
Описание этой кривой в виде полиномиальной параметризации называется точной интерполяцией данного ансамбля.
Заметим, что задача точной интерполяции имеет смысл для любого набора точек. Однако следует иметь в виду, что с ростом числа точек, входящих в ансамль, степень параметризующих его многочленов также растет: для набора из n точек соответствующие многочлены будут иметь степень n − 1. Производить вычислительные операции с такими многочленами весьма затруднительно.
Поэтому на практике, как правило, ограничиваются набором из четырех или даже трех точек, в большинстве случаев характеристики результирующей кривой оказываются вполне приемлемыми.
Теорема 81 (точная квадратичная интерполяция) Для любого опорного ансамбля, состоящего из трех точек A(xA, yA), B(xB , yB ), C(xC , yC ) существует единственная точно интерполирующая его кривая, являющаяся квадратичной параметризацией вида:
a10 + a11u + a12u2 |
, |
p(u) = a20 + a21u + a22u2 |
причем коэффициенты параметризующих многочленов вычисляются одно-
