
0085730_32E51_mosin_v_g_matematicheskie_osnovy
.pdf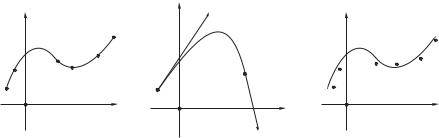
4.2. Интерполяция |
91 |
систем. А это значит, что вычислить координаты точки, лежащей на такой пространственной кривой будет очень сложно.
В то же время, параметрическое описание пространственной кривой отличается от плоского случая только наличием еще одной, третьей координаты:
p(u) = |
p2 |
(u) . |
|
|
p1 |
(u) |
|
|
p3 |
(u) |
|
Это, безусловно, гораздо удобнее с точки зрения построения эффективных алгоримов для движения объектов в графических системах.
Пример 58 Рассмотрим пространственную кривую, описанную параметрически при помощи следующих уравнений:
cos u p(u) = sin u .
u
Нетрудно понять, что точки этой кривой лежат на спирали, которая с равномерным шагом движется вдоль оси Oz. Попробуйте описать ее аналитически (то есть, при помощи системы явных или неявных уравнений). Интересно, что у вас получится.
4.2Интерполяция
При работе с криволинейными объектами в графических системах изначально предполагается, что нам известна (точно или приблизительно) форма кривой. Например, мы можем точно знать, что формируемая процессором кривая должна пройти через данный набор точек (при этом мы можем только догадываться о том, как ведет себя кривая вне этих точек, скорее вего — как-то “хорошо”, не сильно отклоняясь от них).
Требуется же отыскать аналитическое или параметрическое описание кривой, отвечающее известным нам характеристикам, с тем, чтобы передать это описание процессору для дальнейшей обработки (изображения на мониторе или использования в других целях).
|
y |
|
y |
|
y |
|
|
v |
|
||
|
An |
|
|
|
An |
A2 |
A3 |
|
|
A2 |
A3 |
|
|
B |
|
||
|
|
|
|
|
|
A1 |
|
A |
|
A1 |
|
0 |
x |
0 |
x |
0 |
x |
|
|
|
|
||
|
|
|
w |
|
|
Рис. 4.3: Задачи интерполяции.
92 |
Глава 4. Криволинейные траектории |
Пример 59 Записать уравнение кривой, проходящей через три точки: A1(1, 1),
A2(2, 0), A3(4, 4).
Можно предположить, что имеется простое аналитическое описание данной кривой в виде явной функции. Более того, мы будем считать, что эта функция является квадратичной (наши предположения оправдаются тем, что в итоге мы предъявим искомую квадратичную функцию).
Итак, пусть кривая C описывается в виде некоторой, неизвестной нам квадратичной функции:
C : y = ax2 + bx + c .
Тогда, так как C проходит через точки A1, A2, A3, то после подстановки координат этих точек в уравнение кривой, должны получиться тождества:
y(1) |
= 1 , |
|
|
a + b + c = 1 |
, |
|
y(4) |
= 4 ; |
и, следовательно, |
16a + |
4b + c = 4 |
; |
|
y(2) |
= 0 , |
|
4a + |
2b + c = 0 |
, |
|
|
|
|
|
|
|
|
и мы пришли к необходимости решить линейную систему, состоящую их трех уравнений, относительно трех переменных a, b, c. Воспользуемся для ее решения методом Гаусса:
|
|
4 2 1 |
|
0 |
|
−I 4 |
|
|
|
0 |
−2 |
|
|
−3 |
|
−4 |
|
(−1) |
|
||||||||||
|
|
1 |
1 |
1 |
|
1 |
|
|
I 16 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
( 1/3) |
|
||||
|
|
16 |
4 |
1 |
4 |
|
|
|
|
0 |
12 |
|
|
|
15 |
|
12 |
|
|||||||||||
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
− |
|
|
|
− |
|
|
− |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
||
|
0 |
2 |
3 |
|
4 |
II 2 |
|
0 2 |
|
3 |
|
|
4 |
|
|
|
|
|
|||||||||||
|
0 |
4 |
5 |
|
4 |
|
|
|
|
0 0 |
|
1 |
|
|
|
4 |
|
( 1) |
|
||||||||||
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
− |
|
|
|
− |
|
|
− |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1 |
|
−III |
|
|
|
|
|
1 |
1 |
0 |
|
−3 |
(1/2) |
|
|
||||||||
|
0 |
2 |
3 |
|
4 |
−III 3 |
|
|
0 |
2 |
0 |
|
−8 |
|
|
||||||||||||||
|
0 |
0 |
1 |
|
4 |
|
|
|
|
|
|
|
0 0 1 |
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
−3 |
|
− |
II |
|
|
|
1 0 0 |
|
|
1 |
. |
|
|
|
|
||||||||
|
0 |
1 |
0 |
|
−4 |
|
|
0 1 0 |
−4 |
|
|
|
|
||||||||||||||||
|
0 |
0 |
1 |
|
4 |
|
|
|
|
|
0 0 1 |
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, a = 1, b = −4, c = 4. Следовательно, интересующая нас кривая имеет следующее уравнение:
C : y = x2 − 4x + 4 .
Заметим, что при нахождениии уравнения кривой в данном примере мы сделали целый ряд допущений, которые могли бы и не оправдаться. Более того, совершенно очевидно, что они не оправдаются, например, в том случае, если мы поменяем порядок прохождения кривой через те же самые точки: A1, A3, A2. Не существует такой явной функции, график которой проходил бы через эти точки в указанном порядке.
В таких задачах удобнее было бы использовать параметрическую запись кривой (как более универсальную). В связи с этим можно выдвинуть следующую типологию задач (см. рис. 4.3, стр. 91):
1.Известны координаты точек, через которые проходит кривая. Требуется записать уравнения этой кривой в параметрической форме.
2.Требуется записать в параметрической форме уравнения кривой, которая проходит через данный набор точек в заданных направлениях.
4.2. Интерполяция |
93 |
3.Известны координаты некоторого набора точек. Требуется в парметрической форме записать уравнения кривой, проходящей “вблизи” этих точек.
Определение 37 (интерполяция) Задачи приведенных трех типов мы будем называть интерполяционными задачами.
В последней главе, посвященной вопросам интерполяции кривых и криволинейных траекторий (см. главу 6, стр. 139), мы подробно рассмотрим задачи первых двух типов: так называемую точную интерполяцию и интерполяцию в форме Эрмита.
Что же касается задач последнего, третьего типа (построение так называемых B-сплайнов), то их рассмотрение выходит за рамки нашего курса. Ознакомиться с алгоритмами построения B-сплайнов можно в монографии Эдварда Энджела [E].
94 |
Глава 4. Криволинейные траектории |

Глава 5
Математический анализ
Математический анализ1 находит широчайшее применение как собственно в математике, так и в самых разнообразных областях науки и техники (в частности — компьютерной техники). В основе этого математического раздела лежат приципы линеаризации, когда изучение трансцендентных функций2 сводится к изучению их локальных приближений: линейных, квадратичных и т. д.
С геометрической точки зрения данный факт означает, что любую трансцендентную кривую (поверхность) можно с любой степенью точности заменить полиномиальной кривой (поверхностью), что и является нашей конечной целью, так как описание полиномиальных кривых вполне осуществимо в матричной форме (см. главу 6, стр. 139).
При решении задач интерполяции (см. опр. 37, стр. 93), которые в большей степении являются алгебраическими, нежели аналитическими задачами. Аналитические принципы оказываются необходимыми лишь для обескечения гладкости сопряжения сегментов описываемых кривых (требуется, чтобы сегменты в точках сопряжения обладали одинаковыми касательными). Этим (а также тем, что рамки курса весьма ограничены) объясняется то, что мы излагаем лишь начальные главы математического анализа, ограничиваясь геометрическим смыслом производной (см. раздел 5.3, стр. 133).
Порядок изложения является вполне традиционным для большинства вузов. Мы начинаем с краткого представления теории пределов, отталкиваясь, в основном, от понятия предела последовательности (см. раздел 5.1, стр. 96), и далее, опираясь на аппарат бесконечно малых, приходим к понятию непрерывности функции (см. раздел 5.1.6, стр. 113).
Несмотря на то, что в приложениях нам понабодятся лишь производные полиномов, при изучении производных (см. раздел 5.2, стр. 117) мы подробно выводим формулы дифференцирования простейших элементарных функций — техника дифференцирования является важнейшим элементом математической культуры.
1Применяются также альтернативные названия этого раздела математики — дифференциальное и интегральное исчисления, или, исторически более раннее название — исчисление бесконечно малых.
2То есть функций, не являющихся полиномиальными.
95

96 |
Глава 5. Математический анализ |
5.1Пределы. Непрерывность функций
Теория пределов — это теоретический фундамент всего дифференциального исчисления. В данном разделе мы введем основные понятия и обоснуем базовые факты этой теории, что позволит нам в последующих разделах развить аппарат дифференцирования функций и получить некоторые практические приложения.
5.1.1Предел последовательности
Отметим, что последовательности понадобятся нам как вспомогательный инструмент для того, чтобы придти к понятиям предела функции (см. раздел 5.1.5, стр. 108) и непрерывности функций (см. раздел 5.1.6, стр. 113).
Такой порядок излжения методически выгоден: основные свойства пределов функций полностью повторяют соответствующие свойства последовательностей, которые, в свою очередь, вполне очевидны.
Определение 38 (числовая последовательность) Числовой последовательностью называется бесконечный упорядоченный набор чисел:
x1, x2, . . . , xn, . . .
Числовую последовательность мы будем обозначать {xn}, имея ввиду, что индекс n пробегает натуральные значения от 1 до бесконечности.
Для того, чтобы полностью описать числовую последовательность достаточно указать закон, по которому вычисляется ее общий член (то есть член с номером n). И наоборот: если нам известна формула n-го члена последовательности, то мы без труда можем вычислить любой ее член.
Пример 60 Пусть имеется числовая последовательность вида
1, 12 , 13 . . .
Нетрудно сообразить, что тогда ее общий член вычисляется по формуле
1 xn = n .
Пример 61 Наоборот, пусть нам известна формула для вычисления общего чле-
на последовательности:
(−1)nn xn = n + 1 .
Тогда сама последовательность (точнее — ее начальная часть) выглядит следующим образом:
− |
1 |
, |
2 |
, |
− |
3 |
, |
4 |
. . . |
|
2 |
3 |
4 |
|
5 |
||||||
Определение 39 (предел последовательности) Пусть имеется числовая последовательность {xn}.
Число a назывется пределом последовательности {xn}, если для любого положительного ε найдется номер N такой, что для всех номеров n > N выполняется неравенство:
|xn − a| < ε .

5.1. Пределы. Непрерывность функций |
97 |
Если такое число существует, то последовательность {xn} называется сходящейся, и то, что ее предел есть a, обозначается
lim xn = a .
n→∞
В противном случае последовательность называется расходящейся.
Ометим здесь же, что геометрически определение означает, что каково бы ни было число ε, все элементы последовательности, начиная с некоторого номера N , будут попадать в ε-окрестность точки a.
Пример 62 Пусть имеется последовательность следующего вида:
0.9 , 0.99 , 0.999 , . . .
Нетрудно записать фомулу для ее общего члена:
1 xn = 1 − 10n .
Зададимся произвольным, сколь угодно малым положительным числом ε. Тогда соотношение
|xn − 1| < ε , или, что то же самое |
|
1 |
< ε |
10n |
|||
будет выполняться для любого номера n, если только n > lg 1/ε. Следовательно, по определению предела последовательности (см. опр. 39, стр. 96),
lim xn = 1 .
n→∞
Пользоваться данным выше определением предела последовательности (см. опр. 39, стр. 96) крайне неудобно. Далее мы получим свойства сходящихся последовательностей, которые позволят проводить вычисления пределов более технично.
Здесь же мы ограничимся тем, что установим необходимый признак сходимости числовой последовательности.
Определение 40 (ограниченность снизу) Последовательность {xn} называется ограниченной снизу, если существует такое число m, что для всех членов последовательности справедливо:
m < xn .
Определение 41 (ограниченность сверху) Последовательность {xn}
называется ограниченной сверху, если существует такое число M , что для всех членов последовательности справедливо:
xn < M .
Определение 42 (ограниченность) Последовательность {xn} называется ограниченной , если она ограничена и снизу, и сверху.
Пример 63 Рассмотрим несколько последовательностей для того, чтобы проиллюстрировать эти понятия.

98 |
Глава 5. Математический анализ |
1.Последовательность xn = 2nограничена снизу, но не ограничена сверху.
Действительно, существует число m = 0 такое, что m < xn = 2n для любого номера n последовательности {xn}. Отсюда, в силу определения (см. опр. 40, стр. 97) данная последовательность ограничена снизу.
Сдругой стороны, если мы попытаемся подобрать число M , ограничиваю-
щее последовательность {xn} сверху, мы убедимся, что для любого такого числа найдется номер n, для которого xn = 2n > M . Отсюда, в силу определения (см. опр. 41, стр. 97) данная последовательность неограничена сверху.
2.Рассуждая аналогично, можно убедиться, что последовательность xn = −n ограничена сверху, но неограничена снизу.
3.Наконец, последовательность xn = arctg n является ограниченной последовательностью.
Действительно, в силу известных свойств функции арктангенс, для любого значения аргумента справедливо:
−π2 ≤ arctg n ≤ π2 .
Следовательно, существуют такие числа m = −π/2 и M = π/2, что для любого номера n выполняются следующие неравенства:
m < xn < M .
Отсюда, в силу определения (см. опр. 42, стр. 97) данная последовательность ограничена.
Теорема 36 (необходимый признак сходимости) Если последовательность {xn} сходится, то она ограничена.
Доказательство Пусть последовательность {xn} является сходящейся, и пусть ее пределом служит число a. Тогда, по определению (см. опр. 39, стр. 96), для любого положительного ε найдется такой номер N , что для любого n > N будет справедливо:
|xn − a| < ε .
Следовательно, если n > N , то по абсолютной величине члены последовательности меньше мексимального из чисел |a − ε|, |a + ε|:
|xn| < max{|a − ε|, |a + ε|} .
Обозначим A = max{|a − ε|, |a + ε|, |x1|, |x2|, . . . , |xN |}. Тогда, для любого номера n справедливо: |xn| < A. По свойству модуля это означает, что
−A < xn < A для любого номера n .
Таким образом, существуют числа m = −A и M = A такие, что для любого номера n выполняются следующие неравентсва:
m < xn < M .
По определению (см. опр. 42, стр. 97) это означает, что последовательность {xn} является ограниченной.
Теорема доказана.
Трудно сказать, что эта теорема имеет практическое значение. Однако при решении реальных задач широко применяется ее логическое обращение — достаточный признак расходимости.

5.1. Пределы. Непрерывность функций |
99 |
Теорема 37 (достаточный признак расходимости) Если числовая последовательность неограничена, то она расходится.
Доказательство Данное утверждение является логическим обращением необходимого признака сходимости (см. теор. 36, стр. 98). Оба они являются истинными или ложными одновременно.
Так как необходимый признак сходимости нами уже доказан, это означает справедливость и текущего утверждения.
Теорема доказана.
Пример 64 Последовательность xn = 2n является расходящейся, так как выше (см. пример 63, стр. 97) мы установили, что она неограничена.
5.1.2Бесконечно малые и бесконечно большие последовательности
Прежде, чем перейти к вычислению пределов3, в данном разделе мы рассмотрим бесконечно малые и бесконечно большие последовательности и установим их свойства. Они понадобятся нам при изучении свойств пределов (см. раздел 5.1.3, стр. 102).
Определение 43 (бесконечно малая последовательность) Числовая последовательность {αn} называется бесконечно малой, если ее предел равен нулю.
Пользуясь определением сходимости (см. опр. 39, стр. 96), данное определение можно выразить так: последовательность {αn} называется бесконечно малой, если для любого, сколь угодно малого положительного ε найдется номер N такой, что для всех номеров n > N выполняется неравенство:
|αn| < ε .
Определение 44 (бесконечно большая последовательность) Числовая последовательность {An} называется бесконечно большой, если ее предел “равен” бесконечности4.
Пользуясь определением сходимости (см. опр. 39, стр. 96), данное определение можно выразить так: последовательность {An} называется бесконечно большой, если для любого, сколь угодно большого положительного M найдется номер N такой, что для всех номеров n > N выполняется неравенство:
|An| > M .
Теорема 38 (о сумме бесконечно малых) Пусть {αn} и {βn} — две бесконечно малые последовательности. Тогда их сумма {αn} + {βn} — также бесконечно малая последовательность.
3Вычисление пределов обозначается еще одним изящным названием: предельный переход.
4Конечно же, это высказывание не является хоть сколько-нибудь математически корректным. Мы используем его скорее интуитивно.
100 |
Глава 5. Математический анализ |
Доказательство Пусть ε — произвольное, сколь угодно малое положительное число. Тогда ε/2 — также произвольно малое положительное число.
В силу определения бесконечно малой последовательности (см. опр. 43, стр. 99) существуют два номера N , N такие, что
|αn| < ε/2 |
для любого |
n > N , |
|βn| < ε/2 |
для любого |
n > N . |
Если N = max{N , N }, то эти неравенства будут выполняться одновременно при n > N . Сложим неравенства:
|αn| + |βn| < ε/2 + ε/2 = ε для любого n > N .
В силу известного свойства модуля (модуль суммы не превосходит суммы модулей), имеем:
|αn + βn| ≤ |αn| + |βn| < ε/2 + ε/2 = ε для любого n > N .
Итак, для любого, сколь угодно малого положительного ε существует номер N такой, что
|αn + βn| < ε для любого n > N .
По определению бесконечно малой последовательности (см. опр. 43, стр. 99) последовательность {αn} + {βn} является бесконечно малой.
Теорема доказана.
Теорема 39 (о произведении бесконечно малых) Пусть {αn} и {βn}
— две бесконечно малые последовательности. Тогда их произведение {αn} · {βn} — также бесконечно малая последовательность.
Доказательство Рассуждая так же, как и в теореме о сумме бесконечно малых (см. теор. 38, стр. 99), можно придти к выводу, что существует номер N такой, что одновременно выполняются неравенства:
|αn| < ε , |βn| < ε для любого n > N .
Так как ε достаточно мало (можно считать, что ε < 1), то, перемножая эти неравенства, получим:
|αn · βn| = |αn| · |βn| < ε · ε < ε для любого n > N .
Итак, для любого, сколь угодно малого положительного ε существует номер N такой, что
|αn · βn| < ε для любого n > N .
По определению бесконечно малой последовательности (см. опр. 43, стр. 99) последовательность {αn} · {βn} является бесконечно малой.
Теорема доказана.
Теорема 40 (о произведении бесконечно малой и ограниченной)
Пусть {αn} — бесконечно малая, а {fn} — ограниченная последовательности. Тогда их произведение — бесконечно малая последовательность.
