
Лекция дискрет 06
.pdf
Лекция № 6 14 октября 2015 г.

§ 1.4. Мощность множества
Мощность (кардинальное число) множества - некоторое инвариантное свойство, которым характеризуется множество, если отвлечься (абстрагироваться) от природы элементов множества, то есть признаков, по которым они включены в множество, а также от порядка расположения элементов в множестве.
1) Понятие мощности множества
Множество М1 называется равномощным множеству М2 (обозначается М1 ≈ М2), если можно установить некоторое взаимно однозначное отношение между М1 и М2
Th.1.4.1 Отношение |
Система классов эквивалентности |
равномощности множеств – |
{C1,…,Ck,…} для множества Х – |
отношение эквивалентности на разбиение множества Х по |
|
множестве множеств |
отношению эквивалентности R; |
|
любой элемент множества Х входит |
ровно в один класс и классы не пересекаются (§ 1.3)
Мощностью (или кардинальным числом) множества М называется класс множеств, равномощных М
Обозначение мощности множества М: card M или │М│

2) Конечные множества
Множество М называется конечным, если оно равномощно множеству Nk = {1, 2, …, k} натуральных чисел, не превосходящих некоторого натурального числа k. Пустое множество - конечное (по определению). Множество, не являющееся конечным – бесконечное.
Числом элементов конечного непустого множества М называется натуральное число k такое, что М ≈ Nk. Число элементов пустого множества - нуль – по определению.
Мощность конечного множества характеризуется числом элементов в нём: │{ m1, m2, … , mn }│= n, │ │= 0

3) Счётные множества
Множество М называется счётным, если оно равномощно множеству натуральных чисел N = {1, 2, …, n, …} Мощность счётного множества обозначается א0 (алеф-нуль)
Th.1.4.6 Любое бесконечное подмножество N N счётно
Следствие Любое бесконечное подмножество счётного множества счётно
Непосредственно из Th.1.4.6 следует, например, счётность следующих множеств натуральных чисел:
множество чётных чисел { n: n = 2 k, k=1,2,… } множество нечётных чисел { n: n = 2 k+1, k=0,1,2,… }
множество квадратов натуральных чисел { n: n = k2, k=1,2,… } множество простых чисел множество составных чисел
Доказали счётность следующих множеств:
множество рациональных чисел множество алгебраических чисел
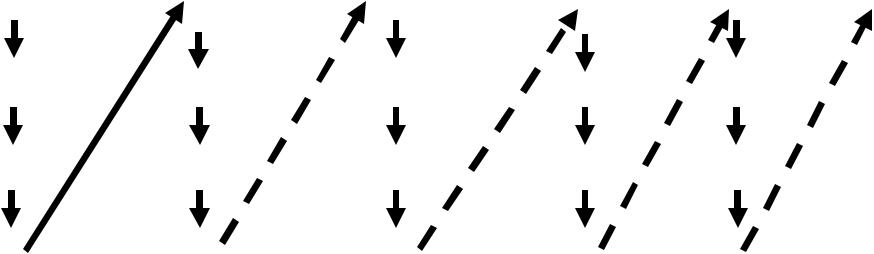
Нумерация объединения конечного множества счётных множеств
а11 |
а12 |
….. |
а1n |
….. |
а21 |
а22 |
….. |
а2n |
….. |
….. |
….. |
….. |
….. |
….. |
аn1 |
аn2 |
… |
аnn |
….. |
Множества занумерованы – от 1 до n. Нумерация объединения идёт по показанной на рисунке схеме: сначала нумеруются первые элементы всех множеств, начиная с множества № 1 и до множества № n, затем вторые …
Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются
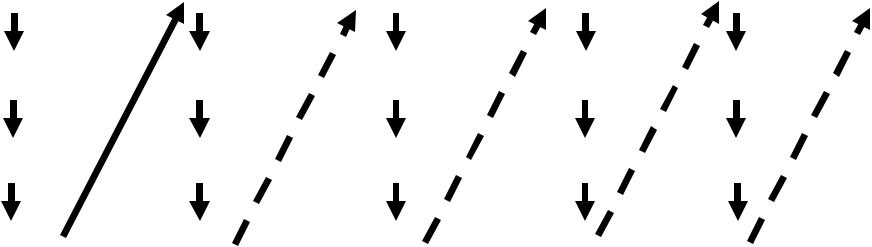
Нумерация объединения счётного множества конечных множеств
а11 |
а21 |
….. |
аm1 |
….. |
а12 |
а22 |
….. |
аm2 |
….. |
….. |
….. |
….. |
….. |
….. |
а1п |
а2n |
2 |
… |
аmn |
….. |
1 |
|
|
|
m |
Множества занумерованы, начиная с № 1, элементы m-го множества имеют номера с 1 до nm. Нумеруем сначала множество № 1, начиная с его первого элемента, затем точно так же множество № 2 и т.д.
Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются
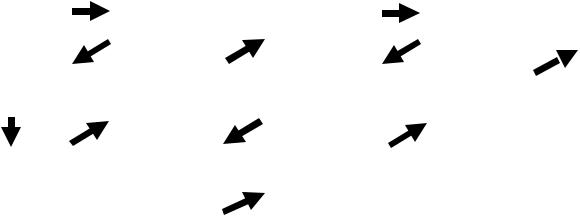
Нумерация объединения счётного множества счётных множеств
а11 |
а12 |
а21 |
а22 |
а31 |
а32 |
….. …..
…..
аn1 |
аn2 |
….. |
….. |
а13 |
а14 |
….. |
а1n |
….. |
….. |
а23 |
а24 |
….. |
а2n |
….. |
….. |
а33 |
а34 |
….. |
а3n |
….. |
….. |
….. |
….. |
|
|
|
|
аn3 |
аn4 |
|
аnn |
….. |
….. |
….. |
….. |
|
….. |
|
|
Множества также занумерованы, начиная с № 1 и т.д. Нумерация объединения идёт по показанной на рисунке схеме – диагональным методом
Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются

4) Континуальные множества
Th.1.4.7 (Теорема Кантора) Множество всех (любых) действительных чисел интервала [0,1] не является счётным
Доказательство Th.1.4.7
Множество действительных чисел интервала [0,1] – это совокупность любых бесконечных дробей вида
0.b1b2b3...bk..., где b1, b2, b3, ..., bk, ... - цифры
Допустим противное: Множество действительных чисел интервала [0,1] счётное, то есть существует его нумерация.
Обозначим действительное число, соответствующее в этой нумерации номеру i, через 0.ai1ai2ai3…aik… и расположим действительные числа интервала [0,1] в порядке номеров.
