Лекция дискрет 09

Лекция № 9 06 ноября 2015 г.

Глава 2. Алгебраические структуры

§ 2.2. Примеры алгебр

Алгебра – множество М с заданной на нём совокупностью операций Ω = { φ1, φ2, … , φm, … }, т.е. структура

A = [ M; φ1, φ2, … , φm, … ]

М– основное множество (носитель) алгебры А

Ω= { φ1, φ2, … , φm, … } – сигнатура алгебры А

Тип алгебры А – вектор арностей её операций

Примеры групп и полугрупп из § 2.1:

[ R \ { 0 }; ] – мультипликативная коммутативная группа

[ N- { 0 } N+; + ] – аддитивная коммутативная группа

[ {Mn}; ] – мультипликативная некоммутативная группа

({Mn} – множество любых квадратных матриц n-ого порядка;- матричное умножение)

[ {Mn}; ] – мультипликативный некоммутативный моноид

(единица – матрица с единичной диагональю; {Mn} – множество невырожденных квадратных матриц n-ого порядка;- матричное умножение)

[ B (M); ] – аддитивный коммутативный моноид (ноль –

пустое множество )

[ B (M); ] – мультипликативный коммутативный

моноид (единица – множество М, выполняющее роль универсума)

y

Модель скрещивания КРС-

моноид [ { a, b, c, d }; ]

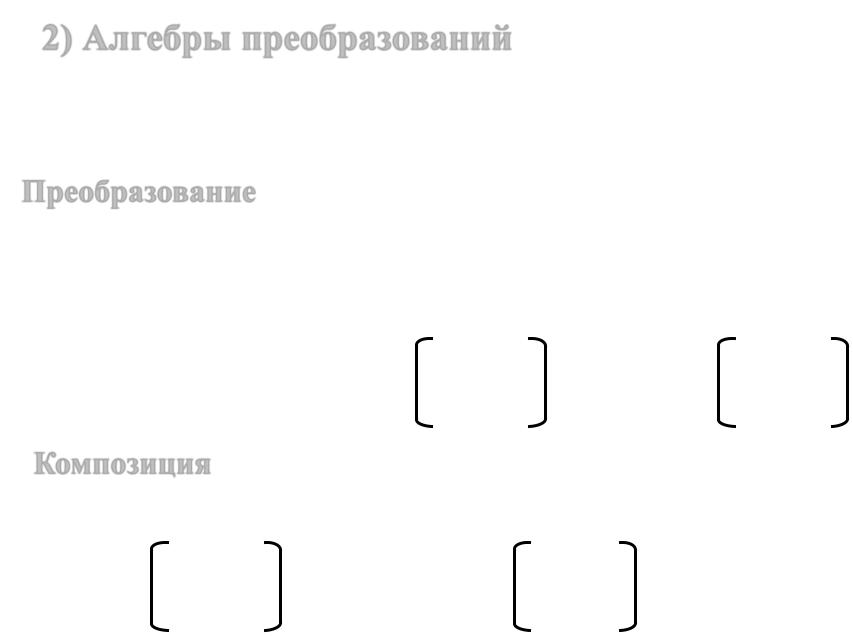
2) Алгебры преобразований

Преобразование множества М – всюду определённое функциональное соответствие f: M Μ (§ 1.2)

Преобразование конечного множества M = { m1, m2, … , mn } - постановка в соответствие каждому элементу mi M элемента mj M того же множества (не требуя при этом сюръективность и инъективность), например:

По построению: операция – ассоциативная. Общее количество преобразований множества M = { 1, 2, 3 } – 33 = 27

Множество всех преобразований T(M) = { α1, α2, … , α27 } в силу своей исчерпывающей полноты замкнуто относительно операции Δ, значит, алгебра [ T(M); ] - полугруппа

Видели на простейшем примере: возможно αΔβ βΔα, значит, в общем случае алгебра [ T(M); ] – некоммутативная

Опять же, в силу своей исчерпывающей полноты множества всех преобразований T(M) = { α1, α2, … , α27 }, в нём имеется, в том числе, тождественное преобразование

Нет инъективности нет гарантии обратного преобразования Итак, некоммутативный моноид преобразований конечного множества M = { 1, 2, 3 }