
Лекция дискрет 13
.pdf

Глава 3. Логические функции
n-арная операция на множестве М – функция φ: Mn M
Логическая функция – n-арная операция на множестве B = {0, 1}, т.е. функция f: Bn B
Множество всех логических функций - P2
Множество всех логических функций n переменных - P2(n)
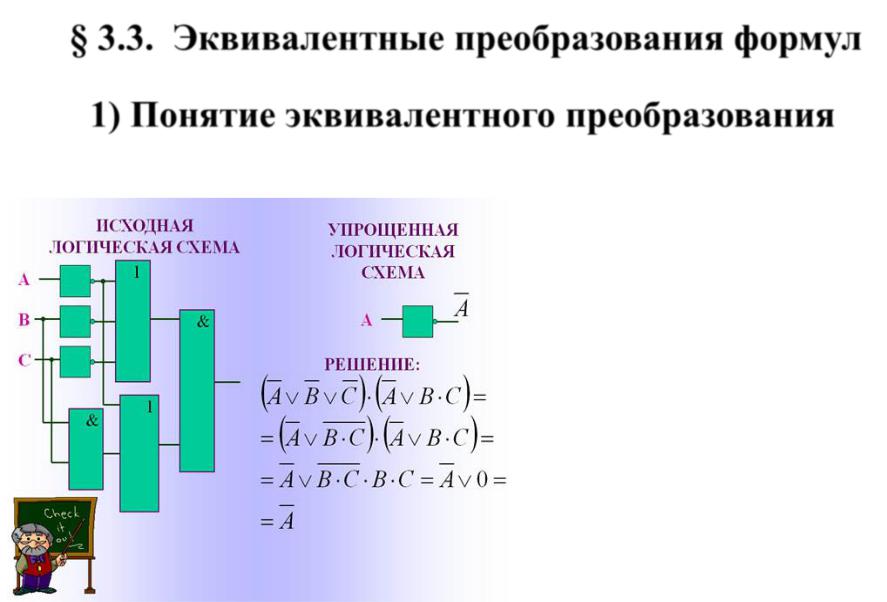
§3.3. Эквивалентные преобразования формул
1)Понятие эквивалентного преобразования
Логические формулы, представляющие одну и ту же логическую функцию, называются эквивалентными или равносильными (§ 3.1)

Из § 3.2: Исходные соотношения (свойства булевских
операций)
Ассоциативность
x1 & (x2 & x3) = (x1 & x2) & x3 |
(3.2.1) |
|
x1 (x2 x3) = (x1 x2) x3 |
|
|
Коммутативность |
|
|
x1 & x2 = x2 & x1 |
x1 x2 = x2 x1 |
(3.2.2) |
Дистрибутивность конъюнкции относительно дизъюнкции
x1 & (x2 x3) = (x1 & x2) (x1 & x3 ) |
(3.2.3) |
Дистрибутивность дизъюнкции относительно конъюнкции
x1 (x2 & x3) = (x1 |
x2) & (x1 |
x3 ) |
(3.2.4) |
Идемпотентность |
Двойное отрицание |
||
x & x = x x x = x |
(3.2.5) |
x = x |
(3.2.6) |
Свойства констант |
|
|
x & 1 = x |
x & 0 = 0 |
|
x 1 = 1 |
x 0 = x |
(3.2.7) |
0 = 1 |
1 = 0 |
|
Правила де Моргана |
|
|
(x1 |
& x2) = x1 x2 |
(3.2.8) |
(x1 x2) = x1 & x2 |
|
|
Закон противоречия |
Закон исключённого третьего |
|
x & x = 0 (3.2.9) |
x x = 1 |
(3.2.10) |

Правило подстановки формулы вместо переменной
При подстановке формулы F вместо переменной x в одно из исходных соотношений (3.2.1) – (3.2.10) или в какую-либо иную логическую формулу должны быть одновременно заменены формулой F все вхождения переменной x в это соотношение (формулу)
Правило замены подформулы на эквивалентную
Если какая-либо формула F содержит F1 в качестве подформулы и F1 эквивалентна F2, то замена F1 на F2 даёт формулу, эквивалентную F, при этом замена всех вхождений F1 в F не требуется
Преобразования формул, использующие исходные соотношения (3.2.1) – (3.2.10), правило подстановки формулы вместо переменной и правило замены подформулы на эквивалентную, называются
эквивалентными преобразованиями
Цель эквивалентных преобразований – приведение формулы к более удобному (каноническому, минимальному, …) виду
2) Полезные соотношения для булевских формул
Поглощение |
|
|
|
x ( x & y ) = x |
(3.3.1a) |
x & ( x y ) = x |
(3.3.1b) |
Склеивание |
( x & y ) ( x & y ) = x |
(3.3.2) |
|
Обобщённое склеивание |
|
||
(x & y) (x & z) (y & z) |
= (x & z) (y & z) |
(3.3.3) |
|
Сопоставление |
x ( x & y ) = x y |
(3.3.4) |
|
Поглощение + Сопоставление |
|
||
x1 f (x1, x2, … , xn) = x1 f (0, x2, … , xn) |
(3.3.5) |
||
3) Эквивалентные преобразования небулевских формул
(A)x y = (¬x & y) (x & ¬ y) = (x y) & (¬x ¬y)
(B)x y = (x & y) (¬x & ¬ y) = (x ¬y) & (¬x y)
(C) x y = ¬x & ¬y |
(D) |
x y = ¬x ¬y |
(E) 0 = x & ¬x (F) |
x y = ¬x y |
(G) 1 = x ¬x |

4) Построение СДНФ |
|
(напоминание - из § 3.1) |
|||
f (x1, … , xn) = |
|
σ1 |
σn |
) |
(▼▼▼) |
f(σ1,…,σn) = 1 |
(x1 |
& … & xn |
|
||
|
|
|
|
|
|
α { 0, 1 }
1 } |
|
0 |
1 |
Было ранее отмечено: x0 = x, x1 = x |
|
{ 0, |
0 |
1 |
0 |
||
|
|||||
x |
|
|
|
|
|
1 |
0 |
1 |
|
||
|
|
||||
|
|
|
|
|
СДНФ (▼▼▼) функции f (x1, … , xn) содержит ровно столько конъюнкций, сколько единиц в векторе значений функции f (x1, … , xn)
Если σi = 1, в качестве xiσi принимается x
Если σi = 0, в качестве xiσi принимается x

Пример построения СДНФ для |
f (w, x, y, z) = (w x) & (y z) |
|||||||||||||||||||
f (x1, … , xn) = |
|
|
|
σ1 |
& … & xn |
σn |
) |
|
|
(▼▼▼) |
||||||||||
|
(x1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
f(σ1,…,σn) = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
|
x |
|
y |
z |
|
f(w,x,y,z) |
||
w |
x |
y |
z |
|
|
f(w,x,y,z) |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
0 |
|
|
|
|
|
1 |
|
0 |
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
1 |
|
1 |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
0 |
|
|
|
|
1 |
|
0 |
1 |
0 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
|
0 |
|
|
|
|
1 |
|
0 |
1 |
1 |
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
0 |
|
|
|
|
|
1 |
|
1 |
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
0 |
1 |
|
1 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
1 |
0 |
|
1 |
|
|
0 |
1 |
1 |
1 |
|
|
1 |
|
|
|
|
1 |
|
1 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
