
Лекция дискрет 13
.pdfДвойственность функций из Р2(1) и Р2(2)
0(x,y) = 0 |
15(x,y) = 1 |
8(x,y) = x y |
14(x,y) = x y |
1(x,y) = x&y |
7(x,y) = x y |
9(x,y) = x y |
6(x,y) = x y |
2(x,y) |
11(x,y) |
10(x,y) = y |
|
3(x,y) = x |
11(x,y) |
2(x,y) |
|
4(x,y) |
13(x,y)=x y |
12(x,y) = x |
|
5(x,y) = y |
13(x,y)=x y |
4(x,y) |
|
6(x,y) = x y |
9(x,y) = x y |
14(x,y) = x y |
8(x,y) = x y |
7(x,y) = x y |
1(x,y) = x&y |
15(x,y) = 1 |
0(x,y) = 0 |
|
|
|
|
0(x) = 0 |
3(x) = 1 |
2(x) = x |
|
1(x) = x |
3(x) = 1 |
0(x) = 0 |
|

Принцип двойственности для булевских формул
Если в булевской формуле Φ, представляющей функцию f, все конъюнкции заменить на дизъюнкции, дизъюнкции
– на конъюнкции, константы 1 – на 0, 0 – на 1, то полученная формула Φ* будет представлять функцию f*, двойственную f
Пример Φ = (¬x & y) (¬x & ¬z) (y & z) Φ* = (¬x y) & (¬x ¬z) & (y z) =
=((¬x & ¬x) (¬x & ¬z) (¬x & y) (y & ¬z)) & (y z) =
=(¬x (¬x & ¬z) (¬x & y) (y & ¬z)) & (y z) =
=(¬x (¬x & y) (y & ¬z)) & (y z) =
=(¬x (y & ¬z)) & (y z) =
=(¬x & y) (y & ¬z & y) (¬x & z) (y & ¬z & z) =
=(¬x & y) (y & ¬z) (¬x & z)
Принцип двойственности
Если в формуле Φ, представляющей функцию f, все знаки функций заменить соответственно на знаки двойственных им функций, то полученная формула Φ* будет представлять функцию f*, двойственную f
Эквивалентное преобразование
Известна эквивалентность формул A B
A = ((x y) x) y B = (x y) (x y)
В силу принципа двойственности имеет место эквивалентность формул A * B *
A * = ((x y) x) y |
B * = ( (x y), (x y)) |
|
4 |
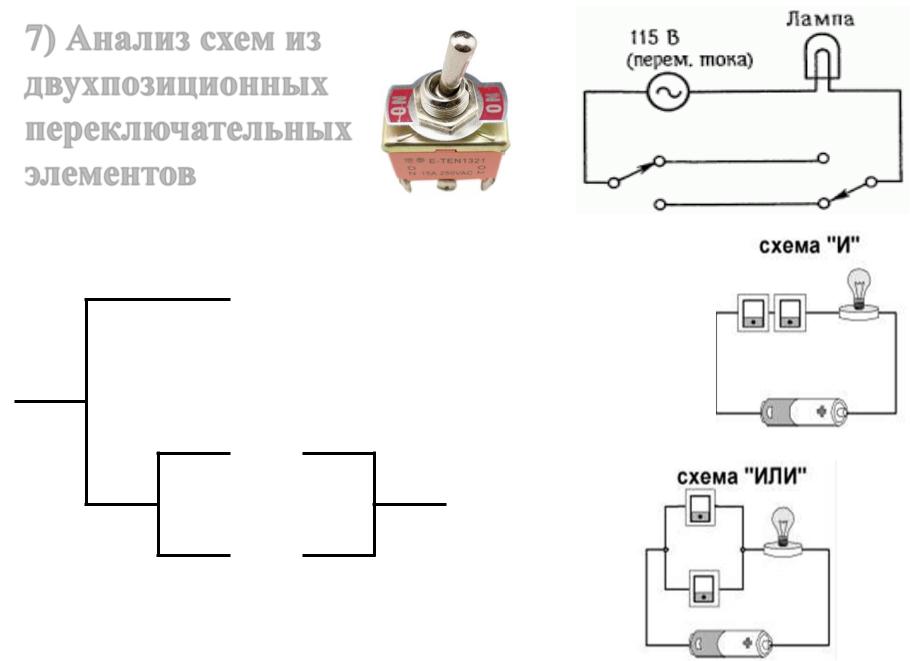
7) Анализ схем из двухпозиционных переключательных элементов
x |
|
y |
|
z
¬y
x
x |
¬y |
|
|
¬ x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|

x |
|
y |
|
z |
|
|
¬y |
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
(x & y) ((x z) & ¬y) = |
||
|
|
|
|||
|
= (x & y) (x & ¬y) (¬y & z) = |
||||
|
|||||
|
|
||||
|
|
|
|
= x (¬y & z) |
|
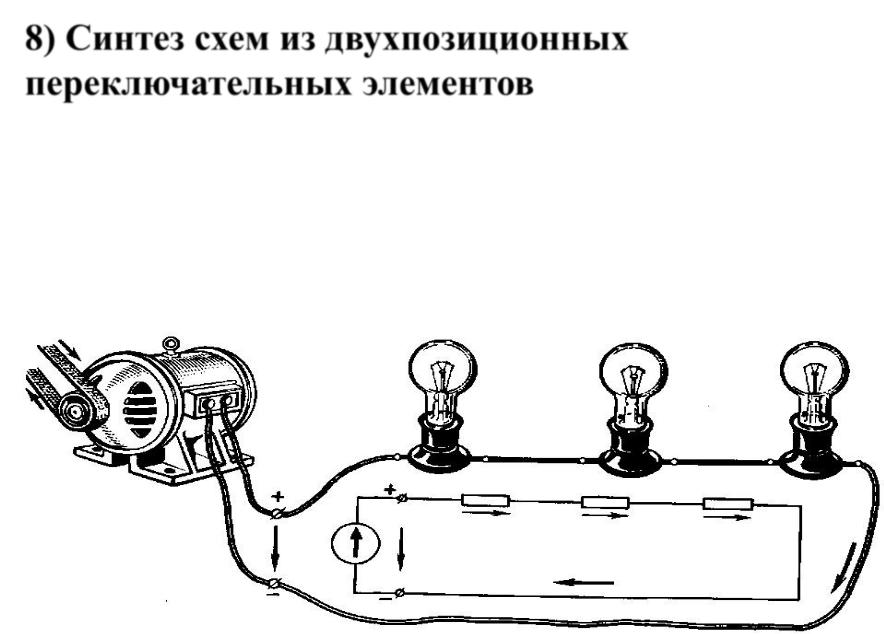
8) Синтез схем из двухпозиционных переключательных элементов
Построить схему электрической цепи для подъезда трёхэтажного дома такую, чтобы двухпозиционным переключателем на любом этаже можно было бы включить или выключить свет во всём подъезде независимо от положения переключателей на других этажах.
Задание на синтез электрической цепи
000 |
0 |
001 |
010 |
100 |
1 |
011 |
101 |
110 |
011 |
110 |
101 |
0 |
001 |
010 |
100 |
010 |
100 |
001 |
1
111 |
111 |
111 |
Отправная точка: 000 – свет в подъезде выключен

Формализация задания на синтез
x |
y |
z |
L |
|
СДНФ (L) = |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
= (¬x & ¬y & z) |
|
0 |
1 |
0 |
1 |
|
(¬x & y & ¬z) |
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
(x & ¬y & ¬z) |
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
||||
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
|
(x & y & z) |
|
|
|
|
|
|
|
|
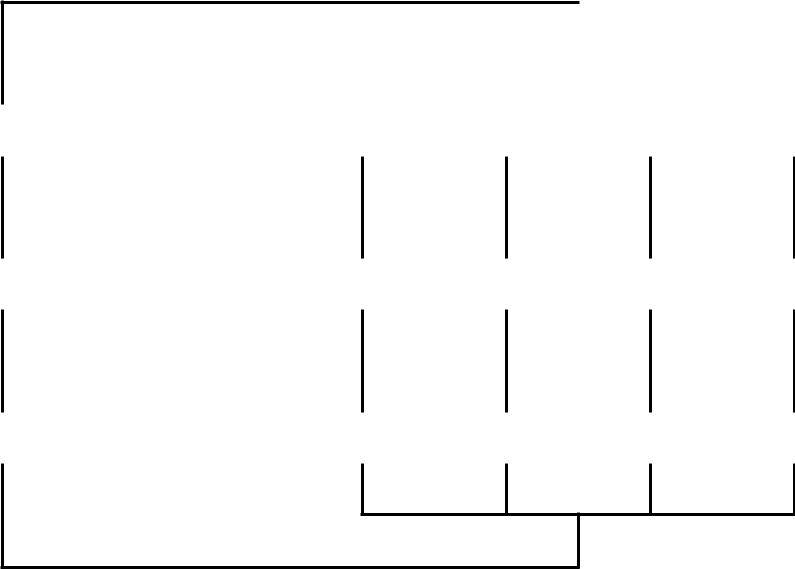
3 этаж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
¬z |
¬z |
z |
|||||
2 этаж |
¬y |
y |
¬y |
y |
|
|
|
|
1 этаж |
¬x |
¬x |
x |
x |
Вопросы к экзамену по дисциплине «Дискретная математика»
1.Основные понятия теории множеств. Операции над множествами: объединение, пересечение,
разность, дополнение. Характеристическая функция множества и её свойства.
2.Основные понятия теории множеств. Декартово произведение множеств. Теорема о мощности декартова произведения множеств.
3.Соответствия и функции. Взаимно однозначные соответствия. Доказательство взаимной однозначности соответствия между булеаном конечного множества и множеством двоичных векторов соответствующей размерности.
4.Соответствия и функции. Свойства соответствий. Критерий существования обратной функции.
5.Отношения. Свойства и виды бинарных отношений. Матрица бинарного отношения, заданного на конечном множестве. Доказательство взаимной однозначности соответствия между бинарными отношениями на конечном множестве и квадратными двоичными матрицами соответствующего порядка.
6.Отношения. Свойства и виды бинарных отношений. Разбиение множества на классы эквивалентности.
7.Равномощность множеств как отношение эквивалентности. Понятие мощности множества.
8.Конечные множества. Теорема о мощности собственного подмножества конечного множества.
9.Конечное множество. Число элементов как характеристика конечного множества.
10.Понятие счётного множества. Счётность бесконечного подмножества счётного множества. Счётность бесконечных множеств рациональных и алгебраических чисел.
11.Понятие счётного множества. Не более чем счётность объединения не более чем счётного
множества не более чем счётных множеств.
12.Теорема Кантора. Понятие континуального множества. Континуальность бесконечных множеств иррациональных и трансцендентных чисел.
13.Обобщённая теорема Кантора. Иерархия мощностей. Примеры гиперконтинуальных множеств.
