
Лекция дискрет 06
.pdf
Соответствие GА В называется взаимно однозначным, если оно удовлетворяет одновременно следующим требованиям: всюду определено; сюръективно; функционально; инъективно
Множество М1 называется
равномощным множеству М2
(обозначается М1 ≈ М2), если существует взаимно однозначное отношение между М1 и М2
Отношение равномощности множеств
– отношение эквивалентности на
множестве множеств
Бинарное отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно
Отношение эквивалентности R на М
m1 |
M |
C1 = { mi M: m1 R mi } |
m2 |
M \ C1 |
C2 = { mi M: m2 R mi } |
……………………..
mk ((…(M \ C1) \ C2)… \ Ck-1
Ck = { mi M: mk R mi }
……………………..
Классы эквивалентности { Ci } по отношению R - разбиение множества М:
1. Ci Cj = i≠j 2. Ci = M
i=1,2,…
Мощностью (или кардинальным числом) множества М называется класс множеств, равномощных М
Мощностью (или кардинальным числом) множества М называется класс множеств, равномощных М
Иерархия мощностей (кардинальных чисел)
Конечные |
Континуумы |
множества |
высших порядков |
Счётные |
Континуальные |
множества |
множества |
Глава 2. Алгебраические структуры
§ 2.1. Основные понятия
Алгебраическая структура [ M; Ω, Θ ]
Алгебра [ M; Ω ] |
|
Модель [ M; Θ ] |
|
|
|
|
сигнатура |
|
Ω – операции на М |
Θ – отношения на М |
|
(l1, l2, … , lp) – тип алгебры |
(s1, s2, … , st) – тип модели |
тип алгебраической структуры

1) Определения
n-арная операция на множестве М – функция φ: Mn Μ
(n – арность операции φ)
Для бинарной (n = 2) операции φ результат её применения к элементам mi M и mj M записывается как
mi φ mj
Внимание! Множество М – не обязательно счётное, запись вида mi M используется только для удобства
Примеры: |
|
φ – соединение (конкатенация) |
|
||
φ – сложение в R |
|
слов (цепочек символов) |
6 φ 7 = 13 |
|
микро φ мир = микромир |
|
|
|

Не всякая функция - операция
Умножение матриц
║С║ = ║A║ ║B║ - операция
Вычисление определителя
квадратной матрицы det (║D║ ) –
функция, но не операция
Векторное умножение векторов A
и B - операция
Скалярное умножение векторов A
и B – функция, но не операция

Бинарная операция φ называется ассоциативной, если для любых элементов mi M, mj M и mk M имеет место равенство
(mi φ mj) φ mk = mi φ (mj φ mk)
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Сложение в R – |
|
|
|
|
Вычитание в R – |
||
|
ассоциативно: |
|
|
|
|
неассоциативно: |
||
|
(6 φ 7) φ 4 = 6 φ (7 φ 4) |
|
(10 φ 5) φ 3 10 φ (5 φ 3) |
|||||
|
|
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
Конкатенация – |
|
Возведение в степень на множестве N – |
|||||
|
ассоциативна: |
|
неассоциативно: |
|||||
|
|
|
|
|||||
(раз φ г) φ ром = |
|
|
(3 φ 2) φ 3 3 φ (2 φ 3) |
|||||
|
= раз φ (г φ ром) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(32)3 3(23)
Бинарная операция φ называется коммутативной, если для любых элементов mi M, mj M имеет
место равенство
mi φ mj = mj φ mi
Примеры:
Сложение в R – коммутативно: |
|
|
Вычитание в R – |
|||||||||||||
|
|
|||||||||||||||
|
|
некоммутативно: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 φ 7 = 7 φ 6 |
|
|
10 φ 5 5 φ 10 |
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
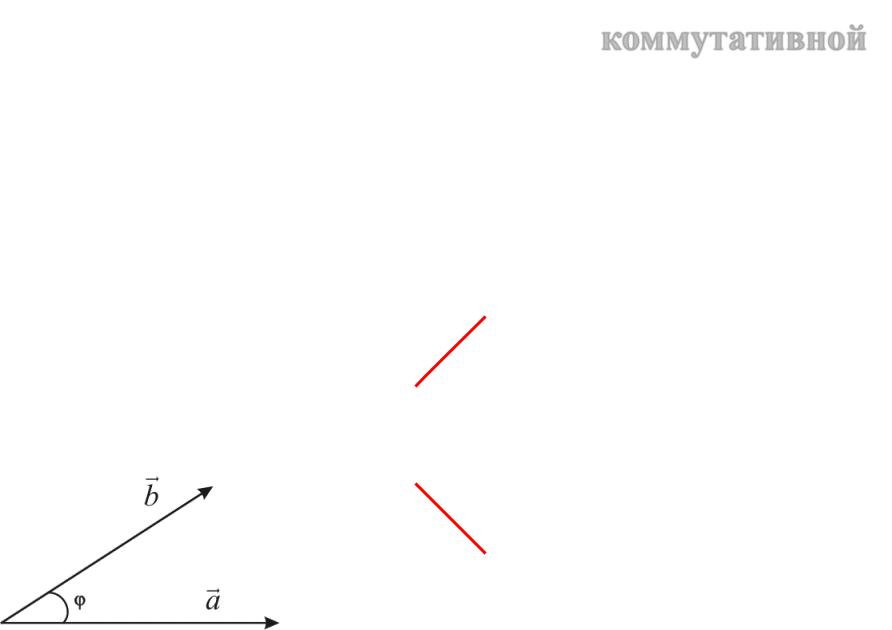
Скалярное произведение |
|
|
|
|
|
|
|
|||||||||
|
|
Конкатенация – некоммутативна: |
||||||||||||||
|
|
|||||||||||||||
векторов – коммутативно: |
|
|
|
|
раз φ гром гром φ раз |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Возведение в степень на N – |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
b) = |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||
|
(a, |
|
|
некоммутативно: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
= │a│ │b│ Cosφ |
|
||||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 φ 2 2 φ 3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Бинарная операция φ называется дистрибутивной слева (справа) относительно бинарной операции ψ, если для любых элементов mi M, mj M и mk M имеет место равенство
(слева) |
mi φ (mj ψ mk) = (mi φ mj) ψ (mi φ mk) |
|
|
(справа) |
(mi ψ mj) φ mk = (mi φ mk) ψ (mj φ mk) |
Примеры: |
ψ- умножение в R |
φ - умножение в R ψ – сложение в R
a (b + c) = (a b) + (a c) (a + b) c = (a c) + (b c)
Дистрибутивность умножения относительно сложения – и слева, и справа
φ – сложение в R a + (b c) (a + b) (a + c)
(a b) + c (a + c) (b + c)
φ - возведение в степень на N
ψ - умножение
справа: (a b)c = ac bc но не слева: ab c ab bc

Элемент е М называется левым (правым) нейтральным элементом относительно бинарной операции φ, если для
любого элемента m M имеет место равенство
 е φ m = m
е φ m = m
«правый»  m φ e = m
m φ e = m
просто «нейтральный»  е φ m = m φ e = m Примеры:
е φ m = m φ e = m Примеры:
На множестве R: 1 – нейтральный элемент относительно умножения, 0 – относительно сложения
На множестве слов нейтральный элемент относительно конкатенации – пустое слово
Возведение в степень на множестве N: правый нейтральный элемент – 1, т.к. для любого n имеет место n1 = n. Левый – не существует: нет такого е, чтобы en = n для любого n
На множестве подмножеств – булеане B (M): нейтральный
элемент относительно операции объединения – пустое множество , относительно пересечения – само множество М, выполняющее в данном случае роль универсума
