2.3 Складна функція

Якщо функція визначена на множині , з областю значень , а функція визначена на множині з областю значень , то функція

називається функцією від функції, або складною функцією, або суперпозицією функцій і , незалежна змінна, проміжна змінна. Областю визначення функції є область , а область зміни — множина . Можлива суперпозиція більшого числа функцій, наприклад

або .

Так можна розглядати як .

Приклади. Подати y як складну функцію від змінної х

1. у= 2z³ , z=tgu , u=.

Розв’язання. Поступово будемо виключати проміжні змінні, підставляючи u= у вираз для z , отримаємо z= tg.Вираз для z підставимо в у= 2z³. В результаті запишемо у=2 (tg)³ =2tg³.

2. ,u= v³ , v=sinw, w=2x+3.

Розв’язання . Із v=sinw і w=2x+3 v=sin(2х+3). Підставимо останній вираз в u= v³ отримаємо

u= (sin(2x+3))³= sin³(2x+3) і, на кінець, =.

Подані нижче складні функції записати за допомогою проміжних аргументів

3. .

Розв’язання. Позначимо u=15х+7, тоді у=u³, або ж, змінивши порядок, у=u³, u=15х+7.

4. .

Розв’язання. y=arcsinu, u=5^v , v=tgw, w=.

Приклади для самостійного розв’язання

Подати змінну у як складну функцію від незалежної змінної х

1. у=,u= 4- 3x.

2. , u= ctgx.

3. , u=, v=cosx.

4. ,u=, w=2x+5.

5. y=arctgu , u=, v=w²+4, w=2^x.

6. Подані далі складні функції записати за допомогою проміжних аргументів у= 7. у=. 8. у=lgtgx. 9. y=. 10. y=.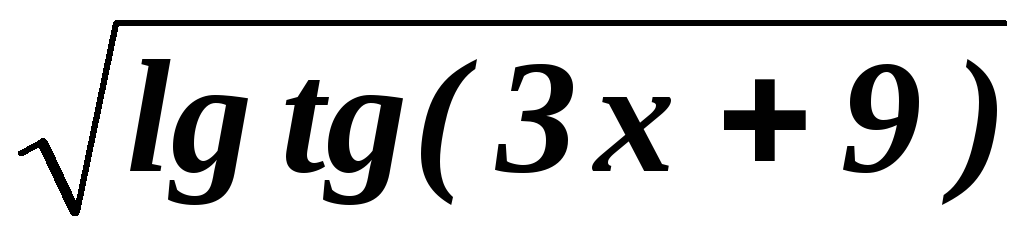

Відповіді. 1. у=2.. 3..

4. . 5.

6. у=,u=4-3x. 7. y=u⁴, u=tgw, w=. 8. y=lgv, v=tgx. 9. y=7^u, u=v³, v=arcsinx. 10. y=, u=lgv, v=tgw, w=3x+9.

2.4 Обернена функція

Розглянемо монотонну функцію визначену на відрізку з областю значень , тобто . Припустимо спочатку, що зростаюча функція:

(див.рис.6)

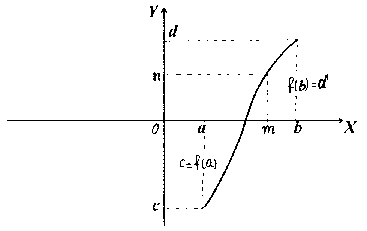
Рис.6.

Найменше значення функція набуває тільки в одній точці, тобто при найменшому значенні аргумента , а найбільше

значення – теж тільки в одній точці, при найбільшому значенні . Всяке інше проміжне значення — в одній і тільки одній точці , що міститься між і . Отже, ми маємо взаємно однозначну відповідність між відрізком осі та відрізком осі . Правило, за яким кожному ставиться у відповідність єдине значення (причому таке, що ) є фукнкцією, визначеною для всіх . Отримана нова функція називається оберненою для функції . Позначимо її буквою , тоді . Таким чином, для всіх . Аналогічно для всіх ,

так що є функцією оберненою для . Очевидно, що теж зростаюча функція, її часто знаходять шляхом розв’язання рівняння відносно . Зауважимо, що графіками функцій і є одна і та ж крива. Функцією називають ще взаємно оберненою для функції .

Позначимо тепер аргумент оберненої функції через , а функцію через , тоді отримаємо в тій же системі координат новий графік .

Графіки функцій та оберненої до неї функції симетричні відносно бісектриси першого–третього координатних кутів. Для цього досить переконатись, що точка графіка і точка графіка , які відрізняються тільки порядком координат, симетричні відносно бісектриси .

Справді, знайдемо спочатку середину відрізка М₁М₂ (див.рис.7):

Рис. 7.

, точка належить бісектрисі . Крім того, трикутник - рівнобедрений (), а, значить,ОМ₀ – є серединним перпендикуляром до відрізка М₁М₂. Отже, точки М₁ і М₂ симетричні відносно бісектриси у=х.

Цю властивість симетріі графіків функції та її оберненої використовують при побудові одного з графіків за відомим іншим.

Зауваження. Всі викладені міркування для монотонно зростаючої функції залишаються вірними для монотонно спадної функції.

Зауважимо ще, що, крім умови монотонності, для існування оберненої функції, потрібна ще умова її неперервності. Це важливе поняття математичного аналізу буде розглядатись пізніше. В даному випадку сприймаємо його інтуїтивною, як суцільність графіка функції, тобто коли ми рисуємо графік на заданому інтервалі, то ручку (олівець) не відриваємо від паперу, на якому зображена частина площини .

Сформулюємо без доведення теорему.

Теорема (про обернену функцію). Нехай – неперервна, строго монотонна (зростаюча або спадна) функція, визначена на відрізку . Нехай , далі, Тоді:

1. існує строго монотонна (зростаюча або спадна) функція , яка є оберненою для , визначена на відрізку , і така, що ;

2. обернена для функція неперервна.

Приклад 1. Розглянемо функцію , яка зростає на

інтервалі . Вона має взаємно обернену функцію . Графіки обох функцій збігаються. При позначенні в останньому співвідношенні аргументу через , а функції через , отримаємо обернену функцію , графік якої симетричний з графіком відносно бісектриси (див. рис. 8).

Рис. 8

Приклад 2. Функція визначена на інтервалі не є ні зростаючою, ні спадною на цьому інтервалі. Отже, згідно означень вона оберненої функції не має. Але якщо розглянемо проміжок , на якому зростає, то оберненою для неї буде функція . На проміжку функція – спадна оберненою для неї — функція (див. рис. 9).

Рис. 9

Сукупність двох однозначних функцій (рис. 9, б)

і можна розглядати, як двозначну функцію:

кожному відповідають два різні значення кореня квадратного і , квадрати яких дорівнюють , тобто і .

Приклади багатозначних функцій зустрічаються в тригонометрії.

Приклад 3. Функція зростає на відрізку шляхом симетричного відображення її графіка відносно бісектриси отримаємо графік функції . (див. рис. 10).

Рис.10

Областю визначення функції є відрізок , а область її значень відрізок , крім того, .

Можна знаходити обернені функції для на інших відрізках, спадання і зростання , в загальному випадку .Кожна з таких обернених функцій визначена на відрізку з областями значень відповідно,.

Сукупність цих обернених функцій дає багатозначну функцію, яка позначається , і, як відомо з тригонометрії, виражається через головне значення за формулою:

Рекомендуємо шляхом симетрії відносно бисектриси побудувати графіки функцій .

Отже , із загальних викладок і розглянутих прикладів 1-3 можна зробити такий висновок : для того щоб знайти обернену функцію для заданої функції, яка задовольняє умовам теореми про обернену функцію необхідно:

1) розв’язати рівняння відносно змінноїх , отримаємо взаємно обернену функцію .

2) у співвідношенні позначити черезу функцію, а аргумент через х , отримаємо обернену функцію .

3) графіки функції і оберненої до неї функції- симетричні відносно бісектрисиу=х.