III. Границі

3.1. Нескінченно малі величини. Границя змінної. Нескінченно великі величини

В цьому розділі при вивчені границь для змінної величини будуть широко використовуватись співвідношення вигляду, . Перш ніж дати їх означення, звернемо увагу на те, що одним із засобів вивчення змінної є порівняння її значення із наперед заданими сталими величинами. Наприклад, вивчаючи зміну температури ми спостерігаємо за зміною стовпчика термометра і відносно зафіксованих поділок шкали можемо судити про підвищення або зниження температури, знайти її значення в даний момент. Значення напруги в електромережі вимірюють за допомогою вольтметра. Зміна положення стрілки відносно фіксованих поділок на шкалі прилада дає нам інформацію про зростання або спадання напруги. За рівнем води в річці, яка може спричинити повінь в даному місці, слідкують за допомогою вертикально закріпленої біля берега рейки з нанесеними на ній поділками. Відносно умовного нуля на рейці, так званого нормального рівня, можна встановити на скільки метрів рівень води підвищився або опустився, прослідкувати за нормалізацією рівня, коли його відхилення від нуля прямують до нуля.

Отже, значення змінної величини весь час порівнюються із наперед заданими сталими величинами, “поділками шкали”. В математичному аналізі значення малої наперед заданої величини прийнято позначати грецькими буквами – епсілон, або – дельта.

Означення 1. Змінна величина х називається нескінченно малою (н.м.) або прямуючою до нуля (позначається ), якщо в процесі зміни абсолютна величина х стане і залишиться меншою , де > 0 – як завгодно мале наперед задане число, тобто

. (1)

Якщо використати символ - будь-який довільний, для будь якого довільного, то означення 1 можна записати в символічній формі:

(2)

Методична порада. Означення 1 легше запам’ятається, якщо постаратись “озвучити” співвідношення (2). Звертаємо увагу на те, що х в означенні змінна величина.

Для кращого розуміння означення 1 рекомендуємо відповісти на такі запитання:

1. Чи можна вважати х н.м., тобто ,якщо умову 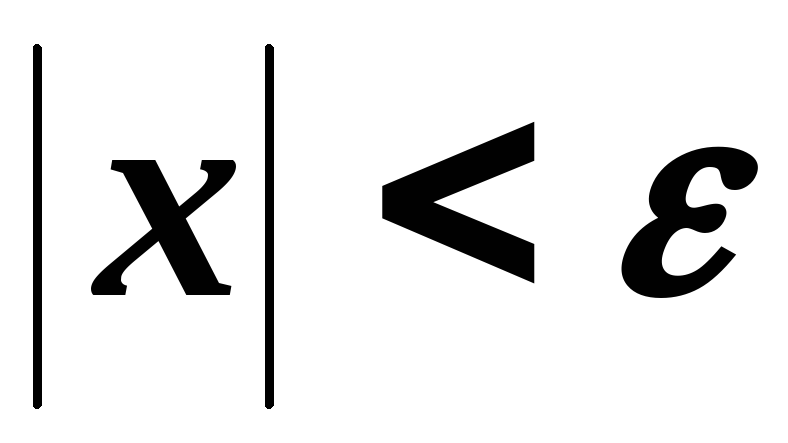в означені 1 змінити на x < ?

2. Чи можна вважати 0,00002 нескінченно малою величиною ?

3. У циліндричну посудину, на стінках якої по вертикалі нанесено поділки, налита рідина, що витікає через відкритий в дні отвір, х – висота рідини відносно дна при цьому зменшується. Фіксуємо поділку ₁, процесі витікання висота х стає меншою ₁ (x< ε₁); фіксуємо нове значення ₂< ε₁, і теж стане х < ₂, і т.д. А тоді в якийсь момент закриємо отвір. Чи є х нескінченно малою величиною?

Означення 2. Змінна х називається прямуючою до числа _, або число єграницею змінної (позначається , або ), якщо їх різниця , нескінченно мала, тобто.

Символічний запис:

(3)

або ж

. (4)

Нерівність (4) згідно з співвідношенням (8) (див. 1.3.) можна замінити еквівалентними

(5)

Означення 3. Інтервал вигляду (5), що містить точку називається -околом (читається: епсілом околом) точки . Позначається - окіл з ценром в точці радіуса . Рівносильним є співвідношення:

(6)

Означення 4. Якщо при функція , то називається нескінченно малою(н.м.) функцією.

Наприклад, н.м. при при ;

при .

Подібно тому, якщо буквою позначаються малі значення для порівняння нескінченно малих, то величини, що зростають, порівнюються із сталими, які позначаються буквою .

Означення 5. Змінна величина називається нескінченно великою або прямуючою до нескінченності (позначається ), якщо в процесі зміни абсолютна величина стане більшою числа , де – як завгодно велике наперед задане число, тобто

В символічному записі співвідношення

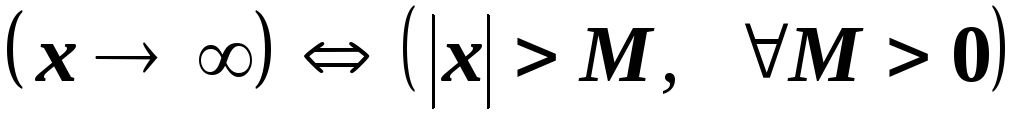(7)

еквівалентні.

Якщо ж і , то пишуть , і якщо , то пишуть .

При вивченні послідовностей приходиться розглядати окремий випадок нескінченно великої змінної , яка приймає значення натуральних чисел . При цьому значення змінної порівнюються з як завгодно великим наперед заданим натуральним числом . Скорочено 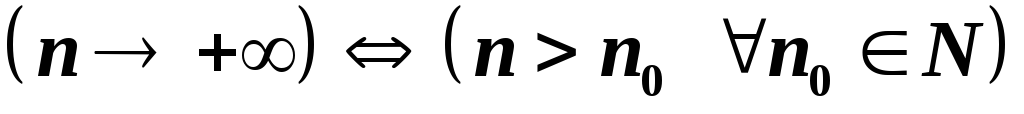, тобто натуральне число є нескінченно великим, або прямуючим до , якщо в процесі зміни воно стане більшим як завгодно великого наперед заданого натурального числа .

Зустрічаються випадки, коли , тоді пишуть .

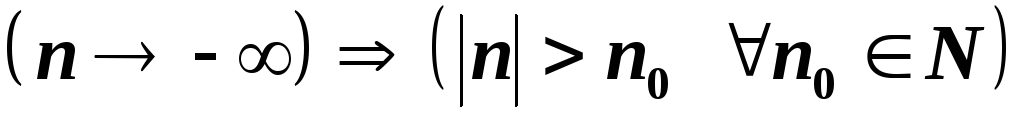Якщо кожному натуральному значенню числа ставиться у відповідність дійсне число , то маємо послідовність чисел або скорочено .

Серед послідовностей теж будемо виділяти н.м.

Означення 6. Якщо при значення деякої послідовності , то така послідовність називається нескінченно малою або, ще говорять, збіжною до нуля.

Точніше, якщо в означенні 6 перейти до нерівності згідно з означенням 1 нескінченно малої, то отримаємо рівносильне означення.

Послідовність називається н.м. (позначається ) при , якщо для довільного як завгодно малого існує номер , який залежить від , такий, що для всіх наступних номерів , виконується нерівність

.

Або якщо ввести ще символ – існує (знайдеться), то в символічному записі маємо:

Приклади.

1. при .

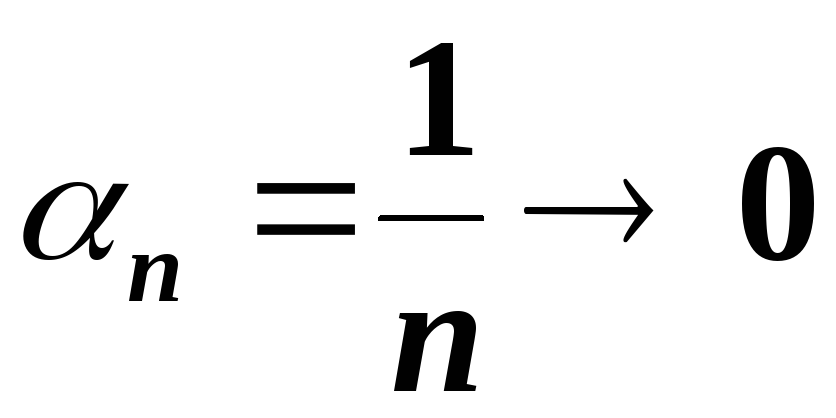2. при .

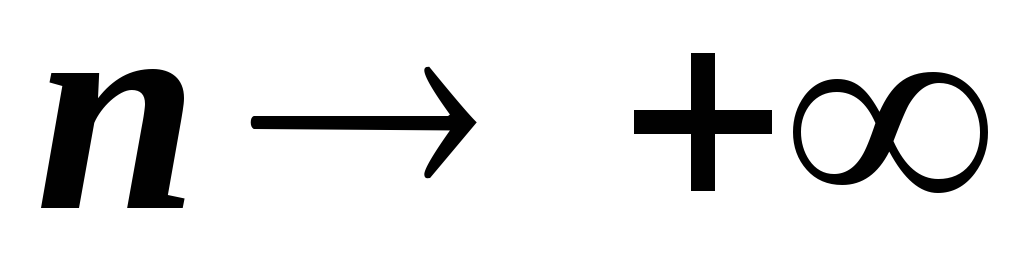За аналогією з означеннями 5 та 6 можна говорити про нескінченно великі функції при та н.в. послідовності при .

Означення 7. Якщо функція при , то її називають нескінченно великою, тобто для існує число таке, що із нерівності

.

Означення 8. Послідовність називається нескінченно великою при , якщо , тобто для натуральне таке, що із нерівності

.

Наприклад:

1. при .

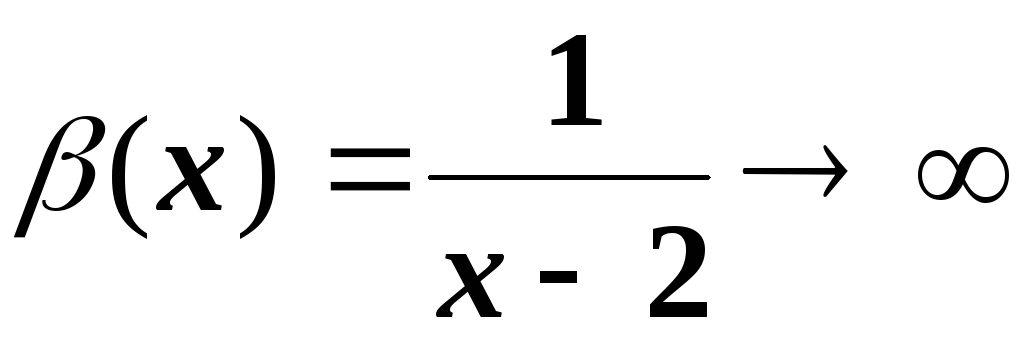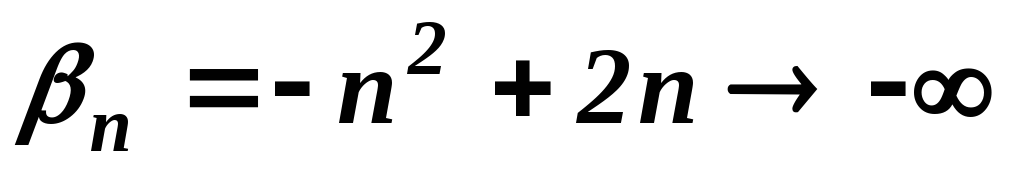2. при .
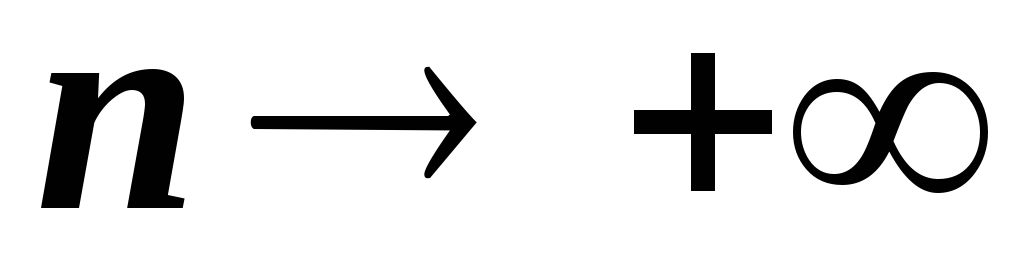