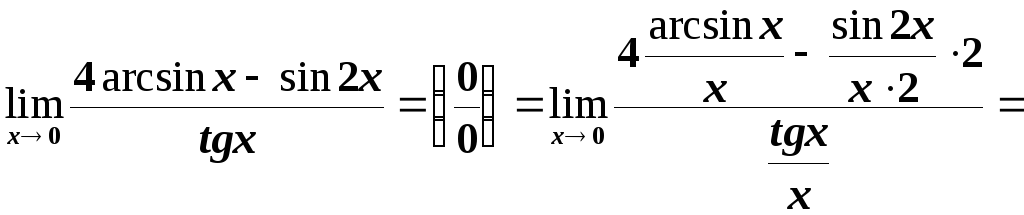- •III. Границі
- •3.1. Нескінченно малі величини. Границя змінної. Нескінченно великі величини
- •3.2. Властивості нескінченно малих, їх зв’язок з
- •3.3 Границя послідовності. Границя функції
- •3.4. Властивості границь
- •3.5. Теореми про існування границь
- •3.6. Односторонні границі
- •3.7. Невизначеності. Приклади знаходження деяких границь
- •3.8. Границя дробово раціональної функції при х
- •Приклади для самостійного розв’язання
- •Приклади для самостійного розв’язання
- •3.11. Друга важлива границя
- •Приклади для самостійного розв’язання.
- •Приклади для самостійного розв’язання
- •1. . 2.. 3..
- •4. . 5.. 6..
3.8. Границя дробово раціональної функції при х
Розглянемо спочатку наступний приклад
= ( добуток н.в. на обмежену є н.в.) = .
З
даного прикладу можна зробити висновок,
що у випадку многочлена із степенями
різних знаків при
![]() може бути невизначеність
може бути невизначеність
![]() .
Щоб її розкрити необхідно винести
старший степінь за дужки. Враховуючи
цей висновок, розглянемо границю дробово
раціональної функції (див. 1.9) при
.
Щоб її розкрити необхідно винести
старший степінь за дужки. Враховуючи
цей висновок, розглянемо границю дробово
раціональної функції (див. 1.9) при
![]() .
.

В кожній з дужок обмежені величини. Можливі три випадки:
 ,
тоді степені скорочуються і границя
дорівнює відношенню коефіцієнтів при
старших степенях
,
тоді степені скорочуються і границя
дорівнює відношенню коефіцієнтів при
старших степенях
 ;
; ,
тоді після скорочення в чисельнику
залишиться
,
тоді після скорочення в чисельнику
залишиться
 ,
тому границя дорівнює ;
,
тому границя дорівнює ;
![]() ,
тоді після скорочення в знаменнику
залишиться
,
тоді після скорочення в знаменнику
залишиться
![]() ,
а обернена до неї
,
а обернена до неї
![]() при
при
![]() ,
в границі отримаємо
,
в границі отримаємо
![]() .
Отже
.
Отже
 (1)
(1)
Приклади для самостійного розв’язання
Знайти границі.
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() .
.
4.
![]() . 5.
. 5.![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8. . 9.
. 9.![]() .
.
10.
 . 11.
. 11. .
.
12.
![]() . 13.
. 13.![]() . 14.
. 14.![]() .
.
15.
![]() .
16.
.
16.![]() .
17.
.
17.![]() .
.
18.
 .
19.
.
19.![]() . 20.
. 20.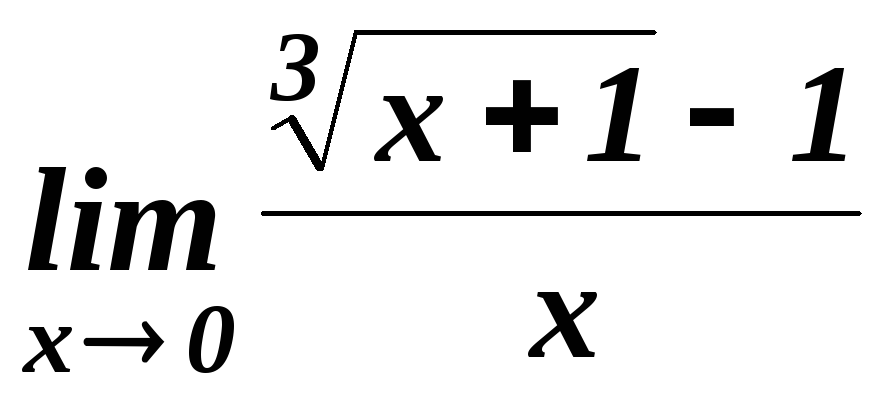 .
.
21.
 . 22.
. 22.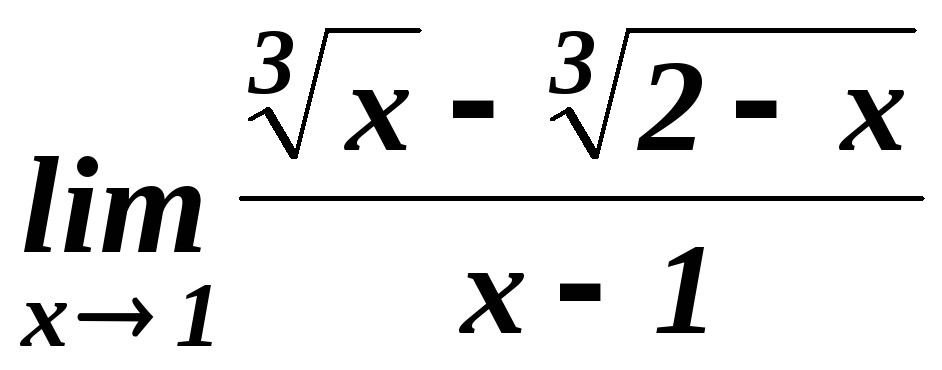 . 23.
. 23.![]() .
.
24.
![]() . 25.
. 25.![]() .
.
26.
![]() . 27.
. 27.![]() .
.
28.
![]() . 29.
. 29.![]() .
.
30.
![]() . 31.
. 31.![]() .
.
32.
![]() . 33.
. 33.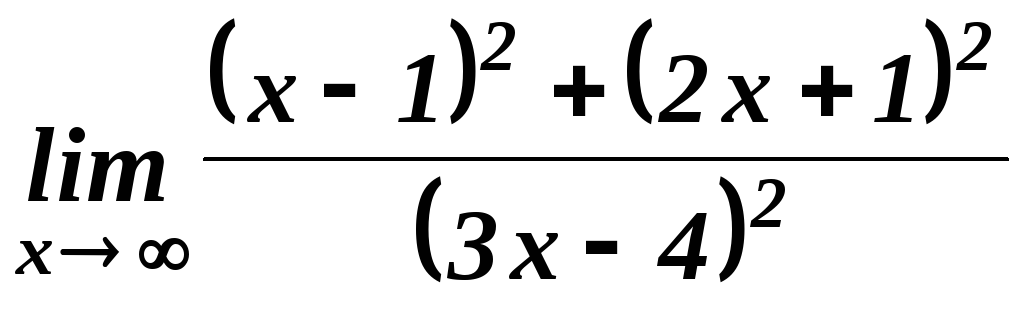 .
.
34.
![]() .
.
Відповіді.
1. 3.
2. 1.
3. 0.
4. -6.
5. 1/4.
6.
-3.
7.3/2.
8.
![]() .
9.
.
9.![]() .
10.
.
10.![]() .
11.
.
11.![]() .
12.
.
12.![]() .
13.
.
13.![]() .
14.
.
14.![]() .
15.
.
15.![]() .
16.
.
16.![]() .
17.
.
17.![]() .
18.
.
18.![]() .
19.
.
19.![]() .
20.
.
20.![]() .
21.2/3.
22.
.
21.2/3.
22.
![]() .
23.
.
23.![]() .
24.
.
24.![]() .
25.
.
25.![]() .
.
26.
![]() .
27.1/2.
28.
.
27.1/2.
28.
![]() .
29.
.
29.![]() .
30.-3.
31.
.
30.-3.
31.
![]() .
32.
.
32.![]() .
33.
.
33.![]() .
34.
.
34.![]() .
.
3.9. Перша важлива границя
Першою важливою називається границя
![]() (1)
(1)
Для доведення (1) будемо виходити із геометричних міркувань (див. рис. 24)
 Рис.
24
Рис.
24
Оскільки
![]() ,
то вважаємо, що кут 2
,
то вважаємо, що кут 2![]() –гострий
центральний кут в колі радіуса
–гострий
центральний кут в колі радіуса
![]() .
Довжина хорди
.
Довжина хорди
![]() очевидно менша довжини дуги
очевидно менша довжини дуги
![]() ,
а дуга
,
а дуга
![]() очевидно менша довжини ламаної
очевидно менша довжини ламаної
![]() ,
тобто
,
тобто
![]()
Із
![]()
![]() .
Довжина дуги
.
Довжина дуги
![]() .
Із
.
Із
![]() довжина дотичної
довжина дотичної
![]() .
Отже, нерівність запишеться
.
Отже, нерівність запишеться
![]()
За теоремою 1 із 2.5 про границю нерівностей маємо
![]()
що рівносильно (1).
На основі (1) отримаємо ще кілька необхідних формул.
![]()
![]() .
(2)
.
(2)


![]() заміна
заміна
![]()
![]()
![]()
![]() .
Якщо
.
Якщо
![]() то
то
![]()
![]() (3)
(3)
Аналогічно
![]() (4)
(4)

![]() (5)
(5)
Приклади.
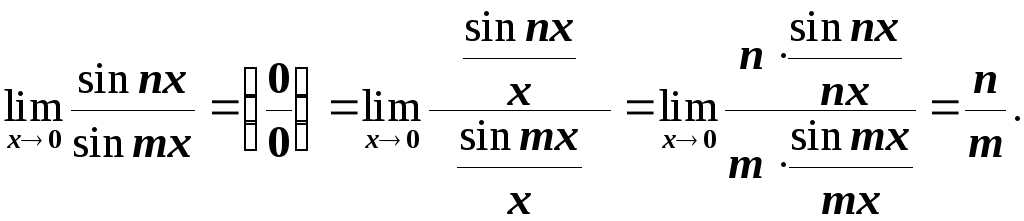


 Заміна
Заміна
 =
=
![]()

![]()
Приклади для самостійного розв’язання
Знайти границі
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() .
.
4.
![]() . 5.
. 5.![]() . 6.
. 6.![]() .
.
7.
![]() . 8.
. 8.![]() . 9.
. 9.![]() .
.
10.
![]() . 11.
. 11.![]() . 12.
. 12.![]() .
.
13.
 . 14.
. 14.![]() . 15.
. 15.![]() .
.
16.
![]() . 17.
. 17.![]() .
.
18.
![]() . 19.
. 19. .
.
20.
 .
.
Відповіді.
1.
![]() .2.
.2.
![]() .3.
.3.
![]() .4.
.4.
![]() .5.
.5.
![]() .6.
.6.
![]() .7.
.7.
![]() .8.
.8.
![]() .
.
9.
![]() .10.
.10.
![]() .11.
.11.
![]() .12.
.12.
![]() .13.
.13.
![]() .14.
.14.
![]() .15.
.15.
![]() .16.
.16.
![]() .
.
17.
![]() .18.
.18.
![]() .19.
.19.
![]() .20.
.20.
![]() .
.
3.10. Натуральні логарифми. Границя, пов’язана з натуральним логарифмом
Розглянемо
функцію
![]() при
при
![]() .
Її область визначення:
.
Її область визначення:
![]() .
Оскільки
.
Оскільки
![]() ,
то функція зростає. При
,
то функція зростає. При
![]() ,
графік проходить через початок координат
(див. рис. 25)
,
графік проходить через початок координат
(див. рис. 25)
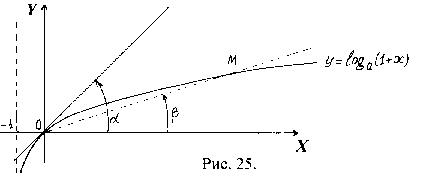
Нехай
![]() довільна точка графіка. Пряму
довільна точка графіка. Пряму
![]() ,
що перетинає графік в двох точках
,
що перетинає графік в двох точках
![]() і
і
![]() ,
називають січною.
Січна
,
називають січною.
Січна
![]() утворює з віссю
утворює з віссю
![]() кут
кут
![]() .
.
Припустимо,
що точка
![]() по кривій наближається до точки
по кривій наближається до точки
![]() ,
тобто
,
тобто
![]()
![]() .
Січна
.
Січна
![]() при цьому буде повертатись навколо
точки
при цьому буде повертатись навколо
точки
![]() ,
кут
,
кут
![]() буде змінюватись. Точка
буде змінюватись. Точка
![]() на кривій може вибиратись як справа,
так і зліва відносно точки
на кривій може вибиратись як справа,
так і зліва відносно точки
![]() .
.
Означення.
Граничне положення січної
![]() ,
що проходить через точку
,
що проходить через точку
![]() ,
при умові що точка
,
при умові що точка
![]() кривої прямує до точки
кривої прямує до точки
![]()
![]() називається дотичною
до кривої
називається дотичною
до кривої
![]() в точці
в точці
![]() .
.
Позначимо
через
![]() кут
нахилу дотичної, тоді згідно означення
маємо
кут
нахилу дотичної, тоді згідно означення
маємо
![]() або
або
![]() (1)
(1)
Тепер
звернемо увагу на положення графіка
![]() в залежності від основи
в залежності від основи
![]() .
Для прикладу розглянемо функції
.
Для прикладу розглянемо функції
![]() При
При
![]() маємо
маємо
![]()
![]()
![]() Схематично положення кривих
Схематично положення кривих
![]() зображено на рис. 26
зображено на рис. 26

Рис.26
В
точці
![]() проведені відповідні дотичні: I, ІІ, ІІІ.
Із рис. 26 зрозуміло, що при збільшені
основи
проведені відповідні дотичні: I, ІІ, ІІІ.
Із рис. 26 зрозуміло, що при збільшені
основи
![]() кут нахилу дотичної до
кут нахилу дотичної до
![]() зменшується, а при зменшені
зменшується, а при зменшені
![]() до
до
![]() цей кут збільшується. Очевидно, що можна
підібрати основу
цей кут збільшується. Очевидно, що можна
підібрати основу
![]() такою, щоб дотична до
такою, щоб дотична до
![]() ,
що проходить через точку
,
що проходить через точку
![]() ,
утворювала з віссю
,
утворювала з віссю
![]() кут в
кут в
![]()
![]() ,
тобто, щоб дотичною стала бісектриса
,
тобто, щоб дотичною стала бісектриса
![]() .
.
Можна
довести, що значення шуканої основи
![]() дорівнює ірраціональному числу
дорівнює ірраціональному числу
![]() яке прийнято позначати буквою
яке прийнято позначати буквою
![]() .
Більш точно
.
Більш точно
![]() .
.
Число
![]() було введено Л. Ейлером1.
було введено Л. Ейлером1.
Логарифми
за основою
![]() називаються натуральними,
замість
називаються натуральними,
замість
![]() пишуть
пишуть
![]() .
.
За формулою переходу до нової основи
![]()
маємо зв’язок між десятковими та натуральними логарифмами
![]() або
або
![]()
Має місце формула
![]() (2)
(2)
Дамо геометричне пояснення формули (2).

Згідно
рис. 27 із
![]() маємо
маємо
![]() кутовий
коефіцієнт січної, але
кутовий
коефіцієнт січної, але
![]() ,
тому
,
тому
![]()
Якщо
![]() ,
то кут нахилу січної
,
то кут нахилу січної
![]() зростає до значення кута нахилу дотичної
зростає до значення кута нахилу дотичної
![]() ,
тому у відповідності із співвідношенням
(1)
,
тому у відповідності із співвідношенням
(1)
![]() Звідки отримуємо (2).
Звідки отримуємо (2).