
- •III. Границі
- •3.1. Нескінченно малі величини. Границя змінної. Нескінченно великі величини
- •3.2. Властивості нескінченно малих, їх зв’язок з
- •3.3 Границя послідовності. Границя функції
- •3.4. Властивості границь
- •3.5. Теореми про існування границь
- •3.6. Односторонні границі
- •3.7. Невизначеності. Приклади знаходження деяких границь
- •3.8. Границя дробово раціональної функції при х
- •Приклади для самостійного розв’язання
- •Приклади для самостійного розв’язання
- •3.11. Друга важлива границя
- •Приклади для самостійного розв’язання.
- •Приклади для самостійного розв’язання
- •1. . 2.. 3..
- •4. . 5.. 6..
3.4. Властивості границь
Теорема
1.
Якщо функцію
![]() при
при
![]() можна представити у вигляді суми сталої
можна представити у вигляді суми сталої
![]() і нескінченно малої
і нескінченно малої
![]() ,
тобто
,
тобто
![]() ,
(1)
,
(1)
то
![]() (
(![]() –
скінченне або
–
скінченне або
![]() ).
(2)
).
(2)
Навпаки,
якщо
![]() ,
то можна записати
,
то можна записати
![]() де
де
![]() н.м. при
н.м. при
![]() .
.
Дійсно,
нехай
![]() тоді
тоді
![]() де
де
![]() н.м.
при
н.м.
при
![]() ,
тобто для
,
тобто для
![]() таке, що із нерівності
таке, що із нерівності
![]() нерівність
нерівність
![]() ,
або
,
або
![]() ,
а це і значить, що має місце рівність
(2).
,
а це і значить, що має місце рівність
(2).
Навпаки,
нехай виконується рівність (2). А це
означає, що для
![]() таке, що із
таке, що із
![]() Позначимо
Позначимо
![]() ,
тоді остання нерівність означає, що
,
тоді остання нерівність означає, що
![]() тобто
н.м.
тобто
н.м.
Наслідок.
Якщо
![]() то
то
![]() тобто
границя сталої величини дорівнює цій
сталій.
тобто
границя сталої величини дорівнює цій
сталій.
Дійсно,
за теоремою 1 маємо
![]() або
або
![]() буде меншою
буде меншою
![]() .
.
Теорема
2.
Нехай існують скінченні границі
![]() і
і
![]() .Тоді
.Тоді![]() ,
,
![]()
![]() за
умови, що
за
умови, що
![]() .
.
Доведемо,
наприклад, другу рівність. За теоремою
1(формула 1) з того, що
![]() і
і
![]() маємо:
маємо:
![]() де
де
![]() і
і
![]() –
н.м. при
–
н.м. при
![]() .
Розглянемо добуток
.
Розглянемо добуток
![]() н.м.
За теоремою 1 маємо, що число
н.м.
За теоремою 1 маємо, що число
![]() є границею функції
є границею функції
![]() при
при
![]() ,
тобто
,
тобто
![]()
![]()
![]()
Рівності перша і третя теореми 2 доводяться аналогічно.
Наслідок.
Сталий множник можна виносити за знак
границі, тобто якщо
![]() то
то
![]()
![]()
оскільки
![]()
Означення
1.
Функція
![]() називається обмеженою при
називається обмеженою при
![]() ,
якщо існує окіл з центром в точці
,
якщо існує окіл з центром в точці
![]() ,
в якому функція
,
в якому функція
![]() обмежена.
обмежена.
Означення
2.
Функція
![]() називається обмеженою при
називається обмеженою при
![]() ,
якщо існує число
,
якщо існує число
![]() таке, що для всіх
таке, що для всіх
![]() ,
які задовольняють нерівності
,
які задовольняють нерівності
![]() ,
функція
,
функція
![]() обмежена.
обмежена.
Теорема
3.
Якщо границя
![]() є скінченною, то функція
є скінченною, то функція
![]() обмежена при
обмежена при
![]() .
.
Доведення
дамо, коли
![]() скінченне.
Із рівності
скінченне.
Із рівності
![]() випливає, що для
випливає, що для
![]() існує
існує
![]() таке, що із
таке, що із
![]() випливає
випливає
![]() тобто
тобто
![]() обмежена.
обмежена.
3.5. Теореми про існування границь
Теорема
1.
Нехай при
![]() (
(![]() скінченне
або
скінченне
або
![]() )
для трьох функцій виконується нерівність
)
для трьох функцій виконується нерівність
![]()
Якщо
існують границі
![]() і
і
![]() ,
які дорівнюють числу
,
які дорівнюють числу
![]() ,
то існує
,
то існує
![]() .
.
Доведення.
Очевидно, що із нерівності
![]()
![]()
За
теоремою 1 із 2.4.
![]() н.м.,
н.м.,
![]() н.м.
при
н.м.
при
![]() .
Це значить, що для довільного
.
Це значить, що для довільного
![]() можна знайти
можна знайти
![]() таке,
що з нерівності
таке,
що з нерівності
![]()
![]()
![]() а, отже,
а, отже,
![]() тобто
тобто
![]() .
.
Теорема
2.
Якщо функція
![]() зростає, і якщо вона обмежена зверху,
тобто
зростає, і якщо вона обмежена зверху,
тобто
![]() ,
,
![]() то ця функція має границю
то ця функція має границю
![]() ,
де
,
де![]() ,
а
,
а
![]() -скінчене
або
-скінчене
або![]() (див.рис.23 ).
(див.рис.23 ).
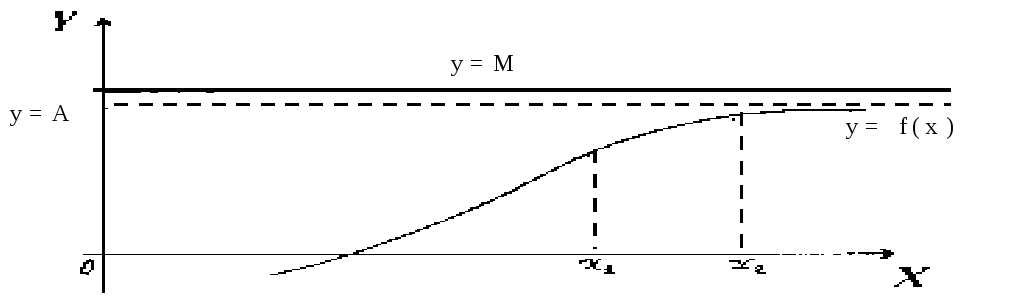
Рис. 23.
Аналогічне
твердження має місце і для спадної,
обмеженої знизу, функції
![]() .
.
3.6. Односторонні границі
Будемо
розглядати процес, коли змінна
![]() ,
але при цьому
,
але при цьому
![]() залишається меншим
залишається меншим
![]() ,
тобто зліва. Цей факт позначають
,
тобто зліва. Цей факт позначають
![]() (зл. – зліва), або зручніше записувати
(зл. – зліва), або зручніше записувати
![]() .
Аналогічно, якщо
.
Аналогічно, якщо
![]() і
і
![]() то будемо говорити, що
то будемо говорити, що
![]() справа, позначають
справа, позначають
![]() або
або
![]() .
.
Означення.
Число
![]() називається лівою
границею
функції
називається лівою
границею
функції
![]() в точці
в точці
![]() ,
якщо вона визначена на деякому
напівінтервалі
,
якщо вона визначена на деякому
напівінтервалі
![]() і для неї існує
і для неї існує
![]() .
.
Аналогічно,
якщо
![]() визначена в напівінтервалі
визначена в напівінтервалі
![]() і
існує
і
існує
![]() ,
то
,
то
![]() називається правою
границею
функції
називається правою
границею
функції
![]() .
.
Ліва – і права границі називають односторонніми. Їх ще прийнято позначати
![]()
Зауваження. Рівності
![]()
еквівалентні
![]() ,
тобто якщо односторонні границі існують
і рівні в точці
,
тобто якщо односторонні границі існують
і рівні в точці
![]() ,
то існує границя функції
,
то існує границя функції
![]() .
.
Якщо ж односторонні границі різні, тобто
![]()
або
хоча б одна з них не існує, тоді не існує
й границя функції
![]() при
при
![]() .
.
3.7. Невизначеності. Приклади знаходження деяких границь
При знаходженні границі ми використовуємо їх властивості, зокрема теорему 2 із 3.4. Можуть виникати такі випадки.
Якщо функція визначена в точці
 ,
то
,
то
 ,
,
тобто
границя функції збігається з її значенням
в точці
![]() .
.
2.
Якщо ж функція в точці
![]() невизначена або
невизначена або![]() ,
то можуть зустрітись співвідношення
вигляду:
,
то можуть зустрітись співвідношення
вигляду:![]()
![]()
![]() ,
які називаютьсяневизначеностями.
,
які називаютьсяневизначеностями.
В
більшості таких прикладів для знаходження
границі над функціями, що стоять під
знаком
![]() необхідно виконати певні тотожні
перетворення, або ще говорять : “позбавитися
невизначеності” або “розкрити
невизначеність”. А там, де невизначеності
не зустрічаються, розв’язання здійснюються
у відповідності теореми 2 та властивостей.
необхідно виконати певні тотожні
перетворення, або ще говорять : “позбавитися
невизначеності” або “розкрити
невизначеність”. А там, де невизначеності
не зустрічаються, розв’язання здійснюються
у відповідності теореми 2 та властивостей.
 Розглянемо
кілька конкретних прикладів з поясненнями
Розглянемо
кілька конкретних прикладів з поясненнями
З
 найти
найти
 згідно теореми 2, а також =
згідно теореми 2, а також =
за наслідками із 2.4
=![]()
![]()
тобто
границя функції збігається з її значенням,
бо
![]() .
.
|
2) |
|
Оскільки
функція в точці
|
=
|
|
=
|
|
Ф-я
|
=
|
.
|
3) |
|
В
точці
|
=
|
|
=
|
|
оскільки
то
на
|
= |
Зауваження. У загальному випадку, якщо
![]() то
необхідно зробити тотожні перетворення
так, щоб
то
необхідно зробити тотожні перетворення
так, щоб![]() і тоді замість
і тоді замість
![]() розглянути
розглянути
![]()
Це,
зокрема, стосується випадку, коли
![]() ,
тоді за допомогою тотожності
,
тоді за допомогою тотожності
![]() (1)
(1)
отримаємо
![]()
де
![]() .
.
Аналогічно
для
![]() береться тотожність
береться тотожність
![]() (2)
(2)
тоді
![]()
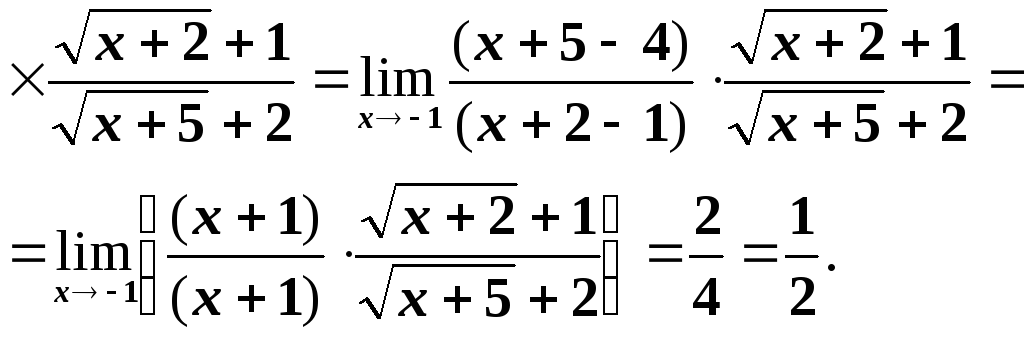
![]()

 6)
6)
![]() див. формулу (2) =
див. формулу (2) =


