VI. Теореми про диференційовні функції

6.1. Теорема Ролля

Теорема. Якщо функціянеперервна на відрізку, диференційовна в інтерваліі приймає рівні значення на його кінцях, тобто, то в інтервалііснує хоча б одна точкатака, що.

Геометрично: знайдеться точка С така, що дотична з цією абсцисою до графіка паралельна осі ОХ (див. рис.39)

Y

f(a) f(b)

a с₁ с₂ b X

Рис.39

Доведення. Оскільки функція неперервна на, то вона досягає на цьому відрізку свого найменшого і найбільшого значень. Якщо б ці значення досягались на кінцях відрізка в точкахі, то за умовою теореминеперервна івипливало б, що функція- стала і тодів кожній точці відрізка. Тому припускаємо, що функціядосягає свого, наприклад, найбільшого значення у деякій точці(див. рис. 39),.

Обчислимо ліву похідну

(1)

і праву похідну

(2)

Згідно диференційовності її ліва і права похідні збігаються, тому із співвідношень (1) і (2) випливає, що.

З рис. 39 видно, що можливі і інші точки, в яких похідна дорівнює нулю .

6.2. Теорема Коші

Теорема. Якщо функції f(x) i (x) неперервні на [a, b] і мають похідні в інтервалі (a, b) і х для х є (a, b), то існує точка , така, що має місце співвідношення:

(1)

Доведення. Розглянемо допоміжну функцію

,

де число підберемо таким, щоб функціязадовольняла теорему Ролля.

Із неперервності на функційівипливає, щотеж неперервна. Крім того, із диференційовностіів інтервалівипливає диференційовність. Залишилось знайти числотаким, щоб, тобто

. (2)

Отже, згідно з теоремою Ролля існує точка , така що, тобто

. (3)

Із рівностей (2) і (3) отримуємо формулу Коші (1).

6.3. Теорема Лагранжа

Теорема. Нехай функція f(x) неперервна на відрізку [a, b] і має похідну на інтервалі (a, b). Тоді існує на інтервалі (a, b) точка c, для якої виконується рівність

Геометричний зміст теореми. Якщо останню рівність записати у вигляді

Y

c

B

A  M

f(a) f(b)

a c b X

то із  АВМ: кутовий коефіцієнт хорди АВ. Згідно теореми існує точка з абсцисою, дотична в якій до графіка буде паралельною хорді.

Якщо покласти у формулі Коші (1) (див. 6.2) (тоді), то отримаємо

- формулу Лагранжа.

6.4. Правило Лопіталя

Теорема 1. Нехай функції f(x) i (x) визначенні і мають похідну в околі точки х₀, а в точці х₀ , тоді якщо існує границя, то існує границя,

причому виконується рівність

Доведення. Функції ізадовольняють умовам теореми Коші в околі точки, тому

,

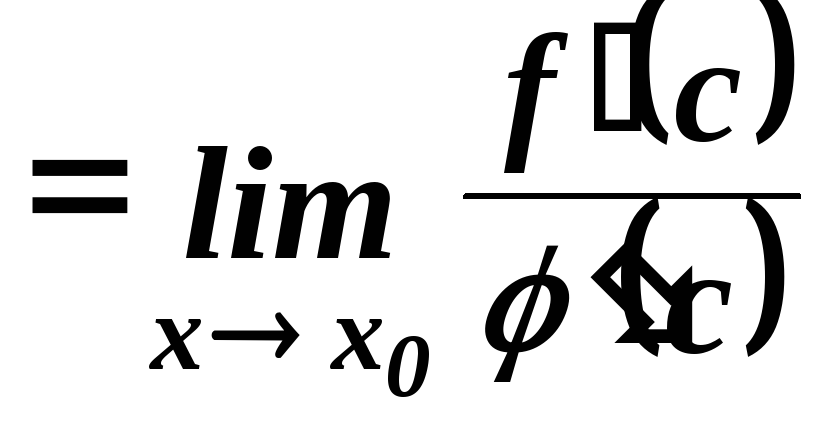де при , а при.

Отже, якщо , то і, тому

.

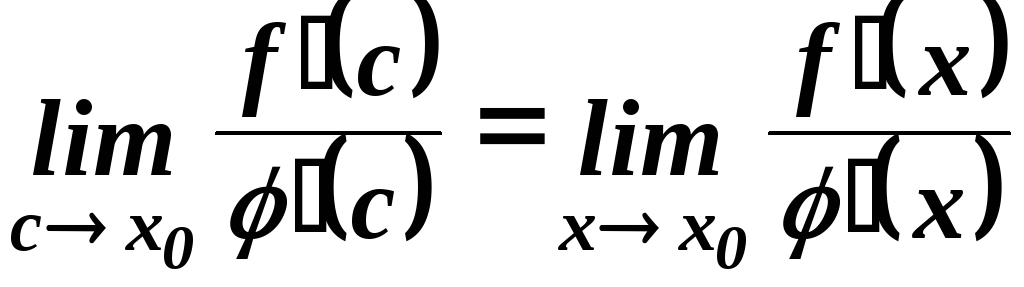В останньому виразі замість змінної можна записати змінну, оскільки границя не залежить від позначення змінної.

За допомогою теореми 1 можна розкривати невизначеність вигляду , причому правило Лопіталя можно застосовувати повторно, якщо в процесі функції і їх похідні задовольняють умовам теореми.

У випадку невизначеності користуються такою теоремою.

Теорема 2. Нехай f i  визначені і мають похідну в околі точки

причому (х), (х)0 в цьому околі, тоді, якщо існує , то існуєі

До викладеного додамо, що правило Лопіталя залишається справедливим при .

Зауваження. За допомогою теорем 1 і 2 розкриваються такі невизначеності:

1. і.

2. Невизначеності іза допомогою алгебраїчних перетворень зводяться до виглядуабо.

3. Невизначеності іза допомогою логарифмування зводяться до невизначеності.

Далі ці випадки розглянемо на прикладах.