Приклади для самостійного розв’язання.

Знайти найменше та найбільші значення функцій на заданих проміжках.

1. . 2..

3. . 4..

5. . 6..

7. .

8. . 9..

Відповіді: 1. . 2..

3. . 4.не існує; .5. . 6.. 7.не існує. 8. не існує. 9. .

7.4. Опуклість і угнутість кривої. Точки перегину

Означення 1. Крива, що описується функцією y=f(x), називається опуклою в інтервалі (a, b) , якщо всі точки кривої лежать нижче довільної її дотичної проведеної в цьому інтервалі.

Аналогічно, якщо всі точки кривої лежать вище довільної дотичної на цьому інтервалі, то крива називається угнутою.

Y

y=f(x)

M

a b c X

рис.46

На рисунку 46 крива y=f(x) – опукла в інтервалі (a, b), і угнута в інтервалі (c,d).

Означення 2. Точка, яка відділяє опуклу частину графіка функції від угнутої називається точкою перегину.

На рис.46 т. М – точка перегину з абсцисою х=b.

Інтервали опуклості і угнутості кривої знаходяться за допомогою слідуючої теореми.

Теорема 1. Нехай y=f(x) має похідні f(x) i f(x) в даному інтервалі. Тоді крива y=f(x) опукла в цьому інтервалі, якщо f(x)<0, i угнута, якщо f(x)>0, для всіх х з цього інтервала.

Так, напр., відповідно на рис.1 f(x)<0, якщо х(a, b), f(x)>0, якщо х(c, d).

Точки перегину знаходяться за наступною теоремою

Теорема 2. (Достатня умова точки перегину). Якщо , або не існує і , змінює знак при переході черезх₀, то х₀ є точкою перегину f(x).

Приклад. Знайти проміжки проміжки опуклості, угнутості та точки перегину функції.

.

Розв’язання. Задана функція визначена для всіх . Знайдемо її похідні

,

.

Щоб знайти інтервали опуклості і угнутості необхідно знайти корені другої похідної, які разом з точками розриву (якщо такі є) розбивають область існування на проміжки.

Якщо на проміжку, то графік угнутий;

Якщо на проміжку, то графік опуклий.

У тих точках, де друга похідна міняє знак, буде точка перегину, за умови, що функція в цій точці неперервна.

Отже, розв’язуємо рівняння

;

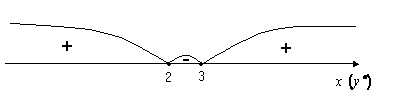
на , графік угнутий;

на , графік опуклий;

на , графік угнутий.

В точках ідруга похідна міняє знак. Це є точки перегину.

.

Приклади для самостійного розв’язання

Знайти проміжки опуклості, угнутості та точки перегину кривих.

1. .

2. .

3. . 4.. 5..

6. . 7..

Відповіді: 1. Опуклість на і на, угнутість на; точки перегинуі.2. Опуклість на і на, угнутість наі на; точки перегину,і.3. Опуклість на і на, угнутість наі на; точки перегину;,.4. Угнутість на і, опуклість на; точка перегину.5. Опуклість на і на, угнутість на; точки перегинуі.6. Опуклість на , угнутість на; точка перегину. 7. Опуклість на, угнутість наі на; точка перегину.

7.5. Асимптоти графіка функції

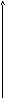Означення. Пряма (l) називається асимптотою графіка функції (кривої (L)), якщо відстань MN від змінної точки кривої (ML) до прямої прямує до нуля, якщо точка М віддаляється в нескінченність, тобто (див. рис. 47,48)

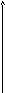Y Y

M

M N

(L) N (L)

(l)

(l) X X

рис.47 рис.48

Асимптоти розрізняють:

1. вертикальні;

2. похилі (окремий їх випадок – горизонтальні).

1. Вертикальні асимптоти. Будемо говорити, що пряма х=а є вертикальною асимптотою графіка функції y=f(x), якщо хоча б одна з односторонніх границь функції дорівнює нескінченості при ха0, тобто

, або .

Y

M N

x x=a X

2. Похилі асимптоти. Знаходяться у вигляді y=kx+b, де

зокрема, якщо k=0, то отримуємо горизонтальну асимптоту y=b, де

Приклади. Знайти асимптоти кривих:

1. . 2..

Розв’язання

1. Із рівняння . Функція існує для.

Вертикальних асимптот функція немає оскільки при і.

Горизонтальних асимптот теж немає, бо .

Знайдемо похилі асимптоти за формулою ,

де .

Знайдемо

;

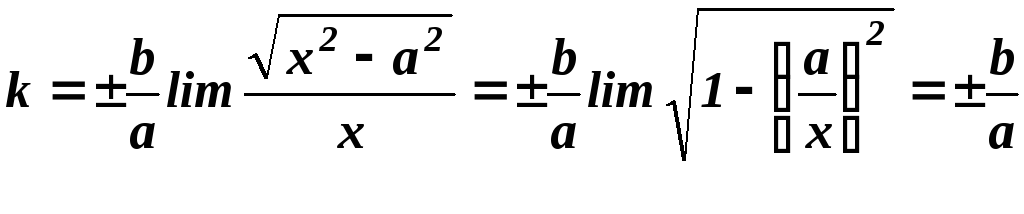Знайдемо вільний член

.

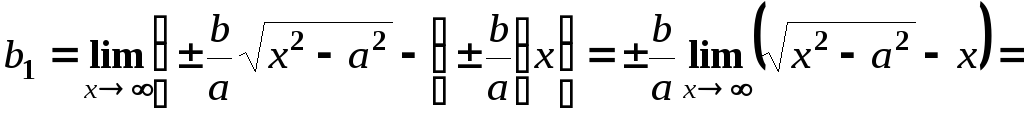
Отже, отримали відомі рівняння асимптот гіперболи

.

2. . Дана функція визначена для , де

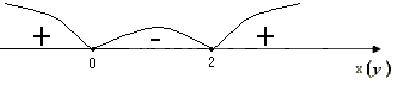
Оскільки

,

то пряма євертикальною асимптотою кривої.

Горизонтальних асимптот крива немає, оскільки

.

Знаходимо похилі асимптоти при і при.

.

.

Отже, існує права похила асимптота .

Знайдемо похилу асимптоту при .

оскільки , то- введемо під корінь

.

.

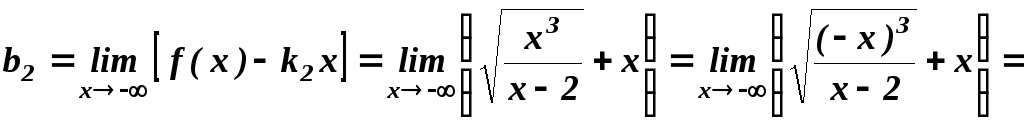
Отже, - ліва похіила асимптота.

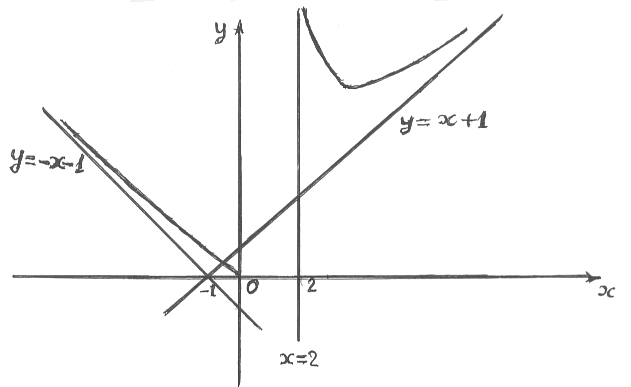
На рисунку зображені асимптоти та графік кривої.