
- •III. Границі
- •3.1. Нескінченно малі величини. Границя змінної. Нескінченно великі величини
- •3.2. Властивості нескінченно малих, їх зв’язок з
- •3.3 Границя послідовності. Границя функції
- •3.4. Властивості границь
- •3.5. Теореми про існування границь
- •3.6. Односторонні границі
- •3.7. Невизначеності. Приклади знаходження деяких границь
- •3.8. Границя дробово раціональної функції при х
- •Приклади для самостійного розв’язання
- •Приклади для самостійного розв’язання
- •3.11. Друга важлива границя
- •Приклади для самостійного розв’язання.
- •Приклади для самостійного розв’язання
- •1. . 2.. 3..
- •4. . 5.. 6..
3.11. Друга важлива границя
Так називається рівність
![]() .
(1)
.
(1)
За
формулою (1) розкривається невизначенність
вигляду
![]() .
.
Для доведення (1) перетворимо співвідношення (2) із 3.10.:
![]()
Перейшовши формально до границі під знаком логарифма в останній рівності, отримаємо
![]()
![]() (2)
(2)
Замінимо
в (2)
![]() (при
(при
![]() )
одержимо рівносильну рівність (1).
)
одержимо рівносильну рівність (1).
Зауважимо, що перехід до границі під знаком логарифма ми здійснили формально. Для його строгого обгрунтування потрібно послатись на властивість неперервності цієї функції. Мова про це піде пізніше.
Приклади


 Виділяємо
цілу частину =
Виділяємо
цілу частину =
![]()
3.

![]() ,
оскільки
,
оскільки

Приклади для самостійного розв’язання.
1.
![]() . 2.
. 2.![]() . 3.
. 3.![]() .
.
4.
![]() . 5.
. 5.![]() .
6.
.
6.![]() .
.
7.
![]() . 8.
. 8.![]()
![]() . 9.
. 9.![]() .
.
10.
![]() .
.
Відповіді.
1.
![]() .
2.
.
2.![]() .
3.
.
3.![]() .
4.
.
4.![]() .
5.
.
5.![]() .
6.
.
6.![]() .
7.
.
7.![]() .
8.
.
8.![]() .
9.
.
9.![]() .
10.
.
10.![]() .
.
3.12. Порівняння нескінченно малих (н.м.)
Відомо,
що дві сталі величини
![]() і
і
![]() можна порівнювати між собою або за
допомогою дій віднімання (
можна порівнювати між собою або за
допомогою дій віднімання (![]() ),
або ділення
),
або ділення
![]() .
При порівнянні н.м.
.
При порівнянні н.м.
![]() і
і
![]() до
згаданих операцій додається ще перехід
до границі, коли
до
згаданих операцій додається ще перехід
до границі, коли
![]() скінченне
або
скінченне
або
![]() .
.
Означення
1.
Якщо відношення
![]() двох нескінченно малих має скінченну
границю
двох нескінченно малих має скінченну
границю
![]() відмінну від нуля, тобто
відмінну від нуля, тобто
![]()
а, значить,
![]()
то
![]() і
і
![]() називаються нескінченно
малими одного порядку.
називаються нескінченно
малими одного порядку.
Приклад.
Функції
![]() і
і
![]() при
при
![]() є н.м. одного порядку, бо
є н.м. одного порядку, бо
![]()
Означення 2. Якщо відношення двох н.м. дорівнює нулю, тобто
![]()
то
![]() називається нескінченно
малою вищого порядку
в порівнянні з н.м.
називається нескінченно
малою вищого порядку
в порівнянні з н.м.
![]() ,
а н.м.
,
а н.м.
![]() є н.м. нижчого
порядку
в порівнянні з
є н.м. нижчого
порядку
в порівнянні з
![]() .
.
Приклади.
Нехай
![]() а
а
![]() і
і
![]() .
Розглянемо
.
Розглянемо
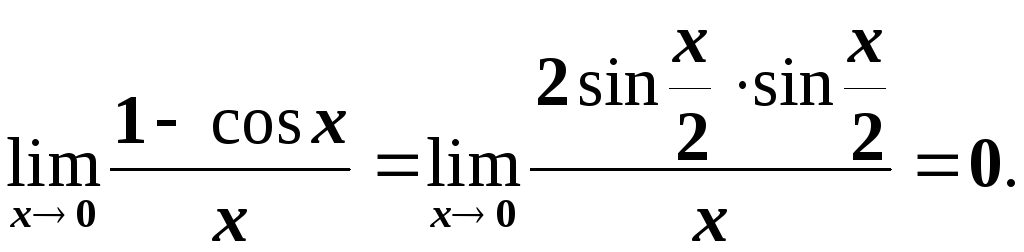
Отже
![]() є н.м. вищого порядку в порівнянні з
є н.м. вищого порядку в порівнянні з![]() .
Це означає, що
.
Це означає, що
![]() швидше зменшується ніж
швидше зменшується ніж
![]() .
Щоб оцінити степінь зменшення однієї
н.м. в порівнянні з іншою, вводиться
поняття порядку зміни.
.
Щоб оцінити степінь зменшення однієї
н.м. в порівнянні з іншою, вводиться
поняття порядку зміни.
Означення
3.
Н.м.
![]() називається н.м.
k-того
порядку
відносно н.м.
називається н.м.
k-того
порядку
відносно н.м.
![]() ,
якщо
,
якщо
![]() і
і
![]() є н.м. одного порядку, тобто
є н.м. одного порядку, тобто
![]()
Приклад.
Нехай
![]() а
а
![]() Оскільки
Оскільки
![]()
то
![]() є
н.м. другого порядку відносно
є
н.м. другого порядку відносно
![]()
Означення
4.
Якщо границя відношення двох н.м.
![]() і
і
![]() дорівнює одиниці, тобто
дорівнює одиниці, тобто
![]()
то
![]() і
і
![]() називаються еквівалентними
н.м. і при цьому пишуть
називаються еквівалентними
н.м. і при цьому пишуть
![]()
![]() .
.
Таблиця основних еквівалентних н.м.
 6.
6.
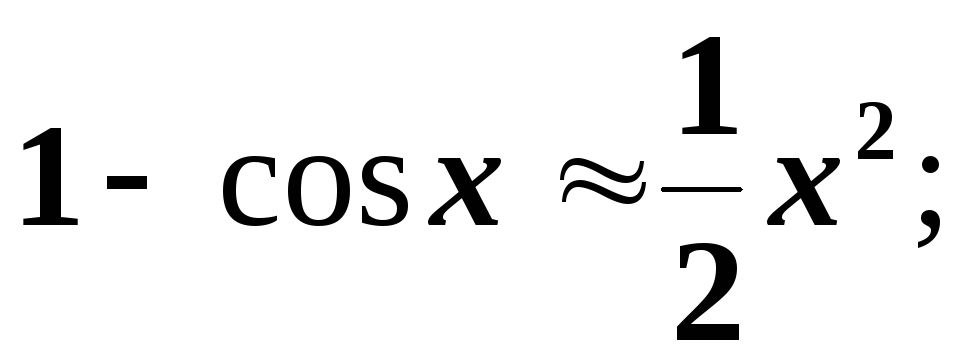
 7.
7.

 8.
8.

 9.
9.


Формули 1–7 були отримані в попередніх параграфах. Розглянемо останню.
![]() Заміна
Заміна
![]() =
=



=
![]()
Наведена таблиця використовувається при розкритті невизначеностей.
Нехай
н.м.
![]() і
і
![]() мають своїми еквівалентними
мають своїми еквівалентними
![]() і
і
![]() ,
тобто
,
тобто
![]() Тоді має місце теорема.
Тоді має місце теорема.
Теорема 1. Границя відношення двох н.м. функцій дорівнює границі відношення їх еквівалентних величин, тобто
![]()
Дійсно,
![]()
Приклад.
![]()
Теорема
2.
Якщо
![]() і
і
![]() –
еквівалентні н.м. (
–
еквівалентні н.м. (![]()
![]() ),
тобто
),
тобто
![]()
то
їх різниця
![]() –
–![]() є н.м. вищого порядку ніж
є н.м. вищого порядку ніж
![]() або
або
![]() .
.
Дійсно,
![]()
![]()
![]()
Теорему 2 треба мати на увазі при знаходженні границь.
Розглянемо
![]()
Хоча
![]() і
і
![]() є н.м. першого порядку в порівнянні з
є н.м. першого порядку в порівнянні з
![]() ,
їх різниця матиме більш високий порядок,
тому використання таблиці
,
їх різниця матиме більш високий порядок,
тому використання таблиці
![]() не допоможе. В даному випадку необхідно
перетворити
не допоможе. В даному випадку необхідно
перетворити

Тепер

Отже,
згідно з означенням 3 можна зробити
висновок, що
![]() є н.м. третього порядку в порівнянні з
є н.м. третього порядку в порівнянні з
![]() .
.

