bludova_t_v_praktikum_z_vishoi_matematiki

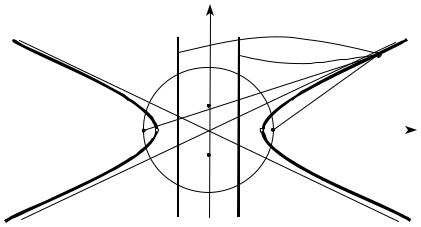
Рис. 5.1

У перерізі прямого конуса площиною П можливі такі криві: коло, якщо площина П b — осі конуса, еліпс, парабола, гіпербола, якщо площина П не проходить через вершину конуса S і відповідно перетинає всі твірні конуса, паралельна одній з його твірних і перетинає обидві порожнини конуса. Такі криві називаються конічними перерізами (рис. 5.1, б).

Якщо параметр а12 = 0, рівняння конічних перерізів, осі симетрії яких збігаються з осями координат декартової площини Оху або паралельні їм, зводяться відповідними перетвореннями до виду канонічних рівнянь залежно від його параметрів (див. таблицю):

Канонічніперерізи, крімпараболи, називаютьсяцентральними кривими.

5.2. Коло

Рівняння кола з центром O1(х0, у0) і радіусом r (позначається: k O1, r ) має вигляд (рис. 5.2):

x x0 2 y y0 2 r2 .

y M3

M1 M2

О1

M

r

Оx

Рис. 5.2

Рівняння кола k O, r з центром у початку координат:

345

х2 + у2 = r2.

Точка М (х1, у1) площини Оху лежить усередині кола, на колі або поза колом, якщо вираз:

Рівнянняназиваєтьсязагальним рівнянням кола, якщоa11 a22 , a12 0,

a132 a232 4a11a33 0.

ЗАДАЧІ

1.Знайти канонічне рівняння кола, заданого загальним рівнянням:

x2 y2 6x 10 y 15 0.

Розв’язання. Утворимо повні квадрати відносно змінних х і у:

x 2 6x 9 y 2 10 y 25 15 9 25

x 3 2 y 5 2 49.

Отже, k(О1, r): О1(3,– 5), r = 7.

5.3. Еліпс

Означення. Еліпсом називається геометрія місце точок, сума відстаней яких до двох заданих точок (фокусів) стала й більша за відстань між фокусами.

Параметри еліпса

Нехай М(х, у) — точка еліпса (рис. 5.3). F1(– с, 0) і F2(с, 0) — фокуси, F1F2 = 2с — міжфокусна відстань; МF1 = r1, MF2 = r2 — фокальні

радіуси: r1 r2 2a 2c .

346

ЗАДАЧА

1.Знайтирівнянняхорди, щопроходитьчерез точку(2, 1) еліпса9х2 +

+25у2 = 225 іподіляєтьсядіаметром2х+ у= 0 пополам.

Розв’язання. Шукана хорда спряжена з діаметром. Тому їхні кутові

коефіцієнти k1k b2 , кутовий коефіцієнт діаметра k1 2 . Тоді ку- a2

5.4. Гіпербола

ли, A1A2 — дійсна вісь (вісь симетрії — головна вісь), ОА1 = ОА2 = а — дійсна піввісь, F1F2 A1 A2 . Координатні осі — осі симетрії, О(0,0) — центр симетрії, B1B2 — уявна вісь.

Прямокутник зі сторонами 2а і 2b, симетричний відносно осей гіперболи і такий, що дотикається до неї в її вершинах, називається основ-

ним прямокутником гіперболи (рис. 5.4).

Число e ac 1 — ексцентриситет гіперболи. Прямі x ae — ди-

ректриси гіперболи відповідно суміжним фокусам F2 (зі знаком «+») і F1(зі знаком «–»).

Формули фокальних радіусів точки М(х, у) гіперболи:

348

Рис. 5.4

Канонічне рівняння гіперболи з центром О(0,0) або О1(х0, у0) має вигляд:

Прямі, що суміщуються з діагоналями основного прямокутника, називаються асимптотами гіперболи (рис. 5.4). Рівняння асимптот

y ba x .

ЗАДАЧІ

1. Знайти канонічне рівняння кривої

5x2 9 y2 30x 18y 9 0

Розв’язання. Оскільки у рівнянні

349

5.5. Парабола

Означення. Параболою називається геометричне місце точок, відстані яких від заданої точки (фокуса) і прямої (директриси) однакові.

Відстань від фокуса параболи до її директриси називається параметром параболи (позначається: р).

y

d

D1 r

350

Рис. 5.5

Канонічне рівняння параболи

Якщо за вісь абсцис узяти пряму, що проходить через фокус і перпендикулярна до директриси, а за початок координат — точку, що є серединою відрізка осі абсцис між фокусом і директрисою (рис. 5.5), то канонічне рівняння параболи має вигляд:

DD1 Oх — директриса параболи; r = MF — фокальний радіус точки

пряма х = х0 — вісь симетрії параболи.

Можливі положення параболи в системі координат Оху зображено на рис. 5.6.

Діаметр параболи — пряма, що проходить через середини паралельних хорд параболи. Усі діаметри параболи паралельні між собою.

351

Рис. 5.6

ЗАДАЧІ

1. Знайти канонічне рівняння кривої 2-го порядку

гляду y y0 2 2 p x x0 .

Перетворення: y2 2 3 y 9 12x 57 9 y 3 2 12 x 4

— це парабола з вершиною О1 (– 4, 3), параметром р = 6; рівняння директриси х = – 1,

F (– 7, 3), у =3 — вісь параболи;

352

6. Дослідження загального рівняння лінії 2-го порядку

6.1. Основні поняття

Нехай маємо загальне рівняння лінії 2-го порядку:

відповідного перетворення координат (паралельного перенесення та повороту) можна подати це рівняння в канонічному вигляді, перейшо-

вши до системи O1 X Y із базисом i1, j1 .

Рівняння (1) визначає не лише геометричні властивості лінії, а й особливості її розміщення на координатній площині. При перетворенні координат розміщення лінії змінюється, а отже, змінюється і її рівняння, при цьому властивості рівняння, які характеризують тип лінії (форму і розміри) лишаються незмінними — інваріантними відносно перетворення координат.

6.2. Еліпс і гіпербола — центрально симетричні лінії 2-го порядку

352

При паралельному перенесенні базису i, j рівняння (1) у системі координат О1хґуґ з початком O1 x0 , y0 перетворюється на таке рівняння:

де — дискримінант рівняння (1),

a11 a12 a13

a21 a22 a23 . a31 a32 a33

За допомогою перетворення координат

x X cos Y sin , y X sin Y cos

дістаємо систему координат О1ХY, яка утворюється поворотом базисуi, j на такий кут , щоб рівняння перетворилося на канонічне:

tg k — кутовий коефіцієнт осі О1Х в системі координат Оху.

Різні випадки дослідження загального рівняння 2-го порядку наведено в таблиці.

353