Раздел 2. Опыт формирования устных вычислительных навыков как основы вычислительной культуры на уроках математики в 5 классе

2.1. Система работы по формированию устных вычислительных навыков

Целью моего проекта является формирование у учащихся устных вычислительных навыков, как основы вычислительной культуры.

Предполагаю, достижение поставленной цели позволит мне, как учителю математики повысить качество знаний по математике, повысить эффективность уроков за счет сокращения времени на вычисления, создать условия для качественной подготовки учащихся к успешному усвоению не только математики, но и других предметов.

Одна из задач, стоящих предо мною: познакомить учащихся с некоторыми приемами упрощенных устных вычислений, которые и помогают формировать вычислительную культуру учащихся. Если на первых этапах знакомства с приемами устных вычислений возникают трудности у некоторых учащихся, то сначала следует проделать вычисления в письменном виде, а уже затем устно. Это даст возможность от приобретения небольшого навыка перейти к большому применению приемов упрощенных и сокращенных вычислений как устно, так и письменно. Все предложенные способы и приемы сокращенных вычислений помогут учащимся в приобретении навыков быстрого счета не только на уроках, но и во внеклассной работе. Необходима постоянная вычислительная тренировка.

Нетрадиционные приемы устного счета основаны на законах математических действий. Отдельные задания помогут восполнить пробелы знаний учащихся по некоторым темам. В наших учебниках этих приемов очень мало, на них нет должного акцентирования и специальной литературы по данному вопросу нет. Поэтому материал по данному вопросу – сборный, из различных источников.

Основная задача - обучить учащихся наиболее эффективным приемам устного счета с дальнейшим использованием их на практике в повседневной жизни, а также при изучении математики и других школьных дисциплин.

Хорошо развитые у учащихся навыки устного счета – одно из условий их успешного обучения в старших классах. Учителю надо обращать внимание на устный счет с того самого момента, когда учащиеся переходят к нему из начальной школы. Именно в 5 классах мы закладываем основы обучения математике наших учеников. Не научим считать в этот период - будем и сами в дальнейшем испытывать трудности в работе, и своих учеников обречем на постоянные обидные промахи.

Для достижения правильности и беглости устных вычислений в течении всего периода обучения на каждом уроке математики необходимо выделять 5-7 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса. Кроме того, приемы устных вычислений, обучение которым требует больших затрат по времени проводятся на лицейских часах, которые проводятся во второй половине дня и направлены на углубленное изучение предмета.

В содержание устной работы, по-возможности, нужно включать упражнения следующих типов: на закрепление и отработку текущего материала; на повторение; с элементами творчества (например, для подготовки к восприятию нового материала, с новой для ребят проблемной ситуацией и т.д.); развивающего характера (в том числе нестандартные упражнения, на сообразительность, занимательные).

Правильно организованные упражнения учащихся в решении задач – важное средство активизации мыслительной деятельности учащихся и развитие их творческих способностей.

Устный счет лучше всего проводить так, чтобы ребята начинали с легкого, а затем постепенно брались за вычисления все более и более трудные! Если сразу обрушить на учащихся сложные устные задания, то ребята обнаружат свое собственное бессилие, растеряются, и их инициатива будет подавлена.

Следует разделять два вида устного счета. Первый – это тот, при котором учитель не только называет числа, с которыми надо оперировать, но и демонстрирует их учащимся на экране проектора или интерактивной доске. Подкрепляя слуховые восприятия учащихся, зрительный ряд фактически делает ненужным удерживание данных чисел в уме, чем существенно облегчает процесс вычислений.

Однако именно запоминание чисел, над которыми производятся действия, - важный момент устного счета. Тот, кто не может удержать чисел в памяти, в практической работе оказывается плохим вычислителем. Учащиеся при этом ничего не записывают и никакими наглядными пособиями не пользуются.

Естественно, что второй вид устного счета сложнее первого. Но он и эффективнее в методическом смысле – при том условии, что этим видом счета удастся увлечь всех учащихся. Последнее обстоятельство очень важно, поскольку при устной работе трудно контролировать каждого ученика. Я стараюсь сделать так, чтобы устный счет воспринимался учащимися как интересная игра. Тогда они сами внимательно следят за ответами друг друга. Но при всем при этом не надо забывать, что этот вид устных упражнений требуют от учащихся большого умственного напряжения, и поэтому сравнительно быстро утомляют их.

Проводимые в начале урока устные упражнения помогают учащимся быстро включиться в работу; в середине или в конце урока служат своеобразной разрядкой после напряжения и усталости, вызванных письменной или практической работой. В отличие от письменных упражнений, содержание устных таково, что решение их не требует большого числа рассуждений, преобразований, громоздких вычислений.

5а класс – это вновь сформированный класс, где собраны учащиеся из трех разных классов и вновь прибывших учащихся из других школ. Соответственно, не смотря на критерии отбора (контрольные работы и тесты по математике, обследование психолога) в пролицейский класс с углубленным изучением математики, физики и информатики дети имеют разный уровень подготовленности по предмету.

На первом уроке в 5 классе я всегда знакомлю учащихся с учебником (Н.Я. Виленкин и др. Математика. 5). Изучение нового материала начинаю с первого урока, но вот первая домашняя необычная: прошу ребят принести к следующему уроку красочно оформленное сочинение «Математика в профессии моих родителей» или «Почему моим родителям математика не нужна». Ребят это всегда удивляет, но они делают это с удовольствием.

На каждом уроке обязательно уделяю 5-7 минут устным упражнениям. Это и решение примеров, направленных, на повторение и закрепление навыков полученных в начальной школе, и на отработку изучаемого материала.

При проведении устного счета придерживаюсь следующих правил:

• Упражнения для устного счета выбираются не случайно, а целенаправленно.

• Задания должны быть разнообразными, предлагаемые задачи не должны быть легкими, но и не должны быть «громоздкими».

• Тексты упражнений, если требуется, готовлю заранее.

• К устному счету должны привлекаю всех учеников.

• При подборе упражнений следует учитываю индивидуальные особенности учащихся (по мере знакомства с ребятами, на основе рекомендаций учителей начальной школы, собственных наблюдений и выводов школьного психолога) .

Применяю дидактические игры. Приведу примеры некоторых из них.

«Помоги старушке подняться по лесенке».

Каждая ступенька результат арифметических действий. Выполнил верно – помог старушке преодолеть лесенку. Можно использовать как в командных соревнованиях, так и в индивидуальной работе.

«Восстанови цепочку».

Н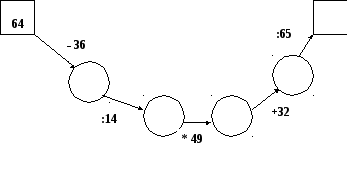еобходимо вписать в кружочки и прямоугольники результаты арифметических действий. Можно использовать для индивидуальной и командной работы.

«Телепатия». Отгадывание задуманного числа.

(Особый вид устных упражнений, когда ничего записывать нельзя. Развивает память, логическое мышление, тренирует внимание)

Учитель предлагает ребятам загадать число, не произнося его вслух. И говорит, что сможет угадать результат после выполнения с этим числом некоторых арифметических действий.

Задумайте двузначное число умножьте его на 2к произведению прибавьте 4сумму умножьте на 4из произведений вычтете 16разность разделите на задуманное число = Должно у всех получиться 8.

Математическая зарядка

Если замечаю, что учащиеся устали. Провожу устный счет в виде математической зарядки. Заранее готовлю несколько карточек с простейшими примерами. Примеры даются с ответами. На одних карточках ответы верные, на других – неверные. Каждое упражнение зарядки состоит их двух движений. Учитель поочередно показывает классу карточки, а ученики делают определенное движение. Например, если верный ответ – руки вверх, неверный – руки вперед. Сначала дети не могут собраться, не попадают в ритм. Но постепенно сосредотачиваются, а темп зарядки увеличивается. И в результате получаю класс, полностью подготовленный к работе.

Дважды в неделю во второй половине дня учащиеся приходят в полном составе на лицейские часы по математике. Это не кружок, а обязательные занятия, где ребята обучаются по программе, которую я разработала специально для учащихся 5 класса. Она направлена на развитие творческих способностей, включает исторический материал, занимательные задачи, изучение материала, не входящего в школьную программу, но интересного и доступного для школьников данного возраста.

Особое место в этой программе занимает материал, позволяющий изучить ребятам нетрадиционные приемы устного счета.

Промежуточное приведение к "круглым" числам.

Если хотя бы одно слагаемое близко к "круглому" числу десятков, сотен, тысяч и т.д. (100, 300, 1000, т.е. (А10n - z), где z - сравнительно мало), то вычисления можно упростить: приведя одно из слагаемых к ближайшему "круглому" числу; выполнив более легкое вычисление с "круглым" и затем учтя поправку.

Использование изменения порядка счета.

При сложении чисел нередко бывает полезно складывать их, начиная со старших разрядов. Тогда в ходе вычисления приходится помнить все более длинное число, но зато мы прибавляем к нему каждый раз только число одно-двузначное. Это существенно облегчает устное вычисление.

Вычитание поразрядно с изменением порядка счета.

При вычитании чисел иногда удобно бывает выполнять вычитание поразрядно, начиная со старших разрядов.

Русский способ умножения.

Один из сомножителей увеличить в несколько раз, а другой во столько же раз уменьшить.

Способ Гаусса.

Гаусс заметил, что всякое умножение чисел можно привести к умножению одного из них на 5; 2 и 1 или на круглые числа, записанные только этими цифрами (и нулем) путем замены другого множителя суммой или разностью соответствующим образом подобранных чисел.

Представление делимого в виде суммы.

Делимое представляют в виде суммы или разности чисел, каждое из которых легко делится на делитель.

Кроме того на лицейских часах провожу дидактические игры подвижные, направленные сохранение физического здоровья, воспитания ответственности, умения работать в команде и еще… - на закрепление навыков устного счета.

Например, «Команда спасателей».

Играют три команды. Необходимо спасти плюшевого мишку, которого «бросила хозяйка». Его местоположение указано в конверте. Конверт спрятан под грудой учебников. Убрать один учебник может только тот, кто верно решит пример на вычисление (три стопки учебников, три столбика примеров на доске). Побеждает команда, которая первой доберется до конверта и спасет мишку (это может быть ученик, закрытый в соседнем кабинете, а в конверте может лежать ключ с биркой, где указан номер кабинета).

Если дети устали можно играть в парную игру.

«Гарри Поттер». Почувствуй себя волшебником.

Чтобы войти в магическую комнату, необходимо открыть дверь, заколдованную Дамблдором (волшебная палочка не помогает и заклинания тоже). Необходимо таблички с числами 5, 10, 15, 20, 25, 30, 35, 40, 45 лежащие у двери разместить в девятиклеточном квадрате на двери так, чтобы в любом столбце, строке или диагонали получилось 75.

«Египетский фараон».

Решение на скорость числовых пирамид. Составить числовую пирамиду, умножая последовательно числа 12, 123, 1 234, …, 123 456 789 на 9 и прибавляя к каждому произведению соответственно 3, 4, 5, 6, 7, 8, 9, 10. В результате вычисления получатся числа: 111, 1 111, 11 111,..., 1 111 111 111.

Для мгновенного контроля провожу игру «Счастливый билет».

Это игра индивидуальная.

Выигрывает тот, кто заполнит карточку первым. Каждый ученик получает набор карточек в конверте, которых обычно больше, чем ответов на большой карточке, тоже вложенной в конверт. Например, маленьких карточек 7-8, а ответов на большой карточке только 6. На маленьких карточках написаны примеры. На большой карточке нарисованы таких же размеров прямоугольники с ответами. Решил пример, закрыл соответствующий прямоугольник маленькой карточкой, лицевой стороной вниз. Если все примеры решены правильно, то обратные стороны наложенных карточек составляют какой-то условный шифр: рисунок, чертеж, букву.

Как уговорить ребенка заниматься математикой, еще и приемы устного счета изучать. Ведь есть калькулятор, компьютер. Да и ребенок собирается стать ветеринаром. Зачем ему математика? Мама у него техничка, отец – слесарь. (Здесь профессии могут быть разными).

Моделируется CASE. У бабушки в деревне заболел поросенок. Внуку ветеринару нужно срочно сделать поросенку инъекцию. Взрослой свинье, которая весит 100 кг, доза лекарственного препарата составляет 2 мг на 20 кг живого веса. А для маленьких поросят половина 1 мг на 10 кг веса. Поросенок весит хкг. Сколько мг лекарственного препарата необходимо ввести поросенку? Свет в деревне отключили, батарейка мобильного телефона не заряжена, калькулятора у бабушки нет. До райцентра 22 км. Из транспортных средств - велосипед. Дорога – ухабы да кочки. Если лекарство не ввести в течение 20мин, поросенок умрет. А у бабушки даже ручки и карандаша в сарае не оказалось. Она пошла искать карандаш и бумагу. Бабушка старенькая, ходит медленно. Время тикает. Что делать? Три команды специалистов должны решить этот вопрос. (Числа могут быть разными, в зависимости от изучаемой темы).

Решение. 1)100 : 20 2 = 10 мг лекарства необходимо свинье.

2) х : 10 1 : 2 мг = мг лекарства необходимо поросенку.

Как определить вес поросенка, если весов у бабушки тоже нет – задание на дом. Создается ситуация поисковая, для учащихся 5 класса довольно сложная. Решение ее потребует творческого похода, поиска решения за страницами учебника математики.

Не менее интересно вовлечение учащихся в проектную работу. Начинаю с провокации. Утверждаю, что числа миллион и миллиард в наш век освоения космоса не очень-то и большие. И прошу найти информацию о происхождении этих слов, т.к. миллион слишком уж похоже на миллиметр и миллиграмм и прошу перевести миллион и миллиард минут в часы, а может даже в дни, года… А если взять 1 млрд кусочков сахара – сколько можно выпить ведерных (10л) самоваров чая, если в чашку 200 г класть 3 кусочка сахара? Сохранятся ли при этом Ваши зубы?

Все эти приемы, формы и методы учитывают психофизиологические особенности учащихся 5-6 класса и успешно используются в работе уже не один год.