Изменение матрицы линейного оператора при переходе от базиса к базису
Пусть линейный оператор : V V в векторном пространстве V имеет матрицу []e в базисе e = (e1 , … , en). Выясним, как изменится эта матрица при переходе к новому базису f = (f1 , … , fn).
Имеем (e) = e[]e , (f) = f[]f , f = eTe, f . Поэтому (f) = f[]f = = eTe, f []f и (f) = (eTe, f) = (e)Te, f = e[]eTe, f . Значит Te, f []f = = []eTe, f и (учитывая обратимость матрицы перехода Te, f) получаем
.
Пример. Пусть : F3 F3 – линейный оператор, имеющий в базисе e = (e1 , e2 , e3) матрицу []e . Найдём []f , если
f = (e1 – e3 , e1 + e2 , 2e2 + e3).
Имеем
Te,
f
=
,
Te,
f–1
=
,
так что
получаем по формуле []f
=
[]e
.
Свойства матрицы линейного оператора
10. Линейный оператор однозначно определяется своей матрицей в любом базисе, т.е. если : V V и : V V – два линейных оператора в векторном пространстве V , причём для базиса e = (e1 , … , en) выполнено равенство []e = []e , то = .
В самом деле, поскольку линейный оператор однозначно определяется значениями на базисных векторах, достаточно доказать, что (e) = (e). Это следует из равенств (e) = e[]e = e[]e = (e).
20. В любом базисе e векторного пространства V матрица суммы линейных операторов : V V и : V V равна сумме матриц этих операторов в том же базисе: [ + ]e = []e + []e .
Действительно, по определению суммы линейных операторов e[+]e = = (+)(e) = (e) + (e) = e[]e + e[]e = e([]e + []e ), откуда и следует доказываемое равенство.
30. В любом базисе e векторного пространства V матрица произведения линейных операторов : V V и : V V равна произведению матриц этих операторов в том же базисе: []e = []e[]e .
В самом деле, по определению произведения линейных операторов имеем e[]e = ()(e) = ((e)) = (e[]e ) = (e)[]e = e[]e[]e , откуда всё следует.
40. В любом базисе e векторного пространства V матрица произведения линейного оператора : V V на скаляр F равна произведению матрицы этого оператора в том же базисе на тот же скаляр:
[]e = []e .
Действительно, по определению произведения линейного оператора на скаляр имеем e[]e = ()(e) = (e) = (e[]e ) = e((In)[]e ) = = e([]e ), что и требовалось.
§ 5. Образ, ядро, ранг и дефект линейного оператора
Пусть V, W – два векторных пространства над одним и тем же полем F, : V W – линейный оператор. Тогда множества
Im() = {w W | v V w = (v)}, Ker() = {v V | (v) = 0W }
называются соответственно образом и ядром линейного оператора (от английских слов Image и Kernel). Графически образ и ядро можно условно изобразить так:
Лемма (об образе и ядре линейного оператора). Для любого линейного оператора : V W справедливы следующие утверждения:
(1) Im() и Ker() – подпространства в W и в V соответственно,
(2) Если e = (e1 , … , en) – базис V, то Im() = L((e1), … , (en)),
(3) Если V = W и e = (e1 , … , en) – базис V, то
Ker() = {v = e[v]e V | []e[v]e=0 nF },
(4) ( инъективен) Ker() = {0V}.
Доказательство. (1) Во-первых, равенство (0V) = 0W показывает, что 0V Ker(), 0W Im(), так что Im() , Ker() . По лемме о подпространстве нужно проверить замкнутость Im() и Ker() относительно сложения и умножения на скаляры.
+: если w1 , w2 Im(), то v1 , v2 V wi = (vi) (i = 1, 2) и w1 w2 = = (v1) (v2) = (v1 + v2) Im() .
Если v1 , v2 Ker(), то (vi) = 0W (i = 1, 2) и (v1 + v2) = (v1)(v2) = = 0W + 0W = 0W , т.е. v1 + v2 Ker().
: если F, w Im(), то v V w = (v) и w = (v) = = (v) Im() .
Если F, v Ker(), то (v) = 0W и (v) = (v) = 0W = 0W , т.е. v Ker() .
Таким образом, Im(), Ker() – подпространства в W и в V соответственно.
(2) Поскольку (ei) Im() (1 i n) , то L((e1), … , (en)) Im(). Для доказательства обратного включения рассмотрим произвольный вектор w Im() и представим его в виде линейной комбинации базисных векторов (e1), … , (en). Пусть w = (v), где v = 1e1+ … + nen V. Тогда w = = (v) = (1e1+ … + nen) = 1(e1) … n(en) L((e1), … , (en)).
(3) Ker() = {v V | (v) = 0V } = { v = e[v]e V | e[(v)]e = 0V } =
= {v = e[v]e V | e[]e[v]e = 0V } = { v = e[v]e V | []e[v]e = 0 nF }, что и требовалось.
(4) () Пусть линейный оператор инъективен: из (x) = (y) следует x = y для любых x, y V. Если v Ker(), то (v) = 0W = (0V) и значит v = 0V , т.е. Ker() = {0V}.
()
Пусть Ker()
= {0V}
и x,
y
V,
причём (x)
= (y).
Тогда (x
– y)
= = (x)
(y)
= 0W
, т.е. x
– y
Ker()
= {0V}
и x
= y
.
Лемма доказана.
Числа dim(Im()) и dim(Ker()) называются соответственно рангом и дефектом линейного оператора и обозначаются через rg(), def() соответственно.
Примеры: 1. Пусть линейный оператор : F3 F3 задан правилом (x; y; z) = (x + 2y; y – z; x + z). Найдём Im(), Ker(), rg(), def().
Выберем стандартный базис e = (e1 = (1; 0; 0), e2 = (0; 1; 0), e3 = (0; 0; 1)) в F 3. Тогда Im() = L((e1), (e2), (e3)), где (e1) = (1; 0; 0) = (1; 0; 1), (e2) = (0; 1; 0) = (2; 1; 0), (e3) = (0; 0; 1) = (0; –1; 1). Итак,
Im() = {1(1; 0; 1)+2(2; 1; 0)+3(0; –1; 1) F3 | 1 , 2 , 3 F} =
= {(1 + 22 ; 2 – 3 ; 1 + 3) F3}.
При
этом векторы
(1; 0; 1), (2; 1; 0), (0; –1; 1)
линейно независимы (т.к.
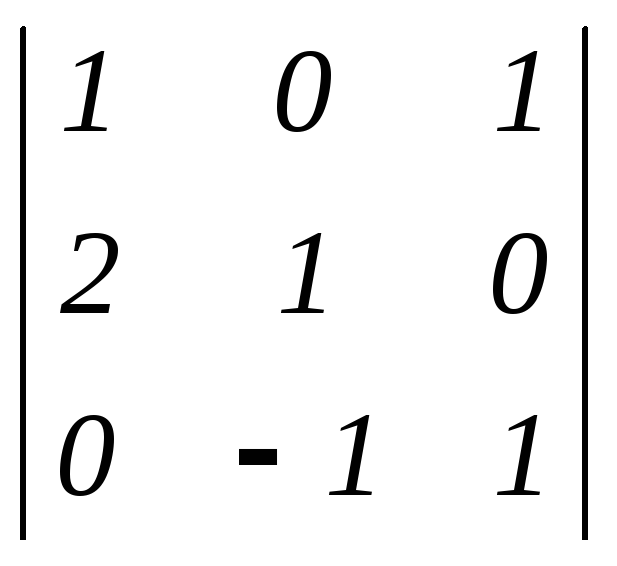
0) и поэтому
образуют базис Im().
Значит,
rg() = dim(Im()) = 3 = dim F3.
Таким образом, Im() = F3 и – эпиморфизм. Далее,
Ker() = { v F3 | (v) = 0} = {(x; y; z) F3 | (x + 2y; y – z; x + z) = (0, 0, 0)} =
=
{(x, y, z)
F3
|
} = {(0, 0, 0)}.
Последнее равенство выполнено т.к. определитель основной матрицы однородной системы линейных уравнений не равен нулю. Таким образом, Ker() = 0, базис ядра не определён, def() = dim(Ker()) = 0, – эпиморфизм и мономорфизм, а значит изоморфизм.
2.
Пусть V
– трёхмерное векторное пространство
с базисом e
= (e1
, e2
, e3),
: V
V
– линейный оператор с матрицей []e
=
. Найдём
Im(),
Ker(),
rg(),
def().
Имеем Im() = L((e1), (e2), (e3)) = L(e1 – e2 , –e1 – e3 , 2e1 – e2 + e3), причём 2e1 – e2 + e3 = (e1 – e2) – (–e1 – e3) , а векторы e1 – e2 и –e1 – e3 линейно независимы (?!). Таким образом,
Im() = L(e1 – e2 , –e1 – e3) = {1(e1 – e2) + 2(–e1 – e3) V | 1 , 2 F} =
= { (1 – 2)e1 – 1e2 – 2e3 V | 1 , 2 F }.
Поэтому rg() = dim Im() = 2 < dim V и не является эпиморфизмом.
По лемме об образе и ядре получаем:
Ker()
= {v
= 1e1
+ 2e2
+ 3e3
V
|
}.
Решаем полученную систему:
Таким
образом, общее решение системы {
F3
| 3
F}
и
Ker() = {v = –3e1 + 3e2 + 3e3 V | 3 F} =
= {v = 3(–e1 + e2 + e3 ) V | 3 F)}.
Базисом ядра будет вектор –e1 + e2 + e3 V, def() = dim Ker() = 1.
Рассмотренные примеры показывают, что для оператора в n-мерном арифметическом пространстве справедливы формулы
dim(Im()) + dim(Ker()) = n, rg() + def() = n.
Оказывается, что имеет место общая
Теорема (о сумме ранга и дефекта линейного оператора). Для любого линейного оператора : V W верно dim(Im()) + dim(Ker()) = dim V, т.е. rg() + def() = dim V.
Д
оказательство.
В случае Im()
= {0W}
имеем
rg()
= 0, Ker()
= V,
def()
= dim V
и доказываемые
формулы очевидны. Если же Ker()
= {0V},
то
– мономорфизм,
dim(Im())
= dim V
, и формулы также выполняются. Таким
образом, можно предполагать, что Im()
{0W}
и
Ker()
{0V}.
Пусть w = (w1 , … , wk) – базис Im() {0W}. Тогда найдутся vi V со свойствами wi = (vi) (1 i k). Пусть, кроме того, k = (k1 , … , ks) – базис Ker() {0V} и e = (v1 , … , vk , k1 , … , ks). Докажем, что e является базисом V. Тогда соотношение dim V = s + k = dim(Im()) + dim(Ker()) станет очевидным.
Линейная независимость: если 1v1 + … + kvk + 1k1 + … + sks = 0V, то
0W = (0V) = 1(v1) … k(vk) 1(k1) … s(ks) =
= 1w1 … kwk ,
откуда (т.к. w – базис Im()) получаем 1 = … = k = 0. Значит, будет верно 1k1 + … + sks = 0V и (т.к. k – базис Ker()) 1 = …= s = 0, что и требовалось.
Система образующих: Пусть v V. Тогда (v) Im() , и значит, найдутся такие 1 , … , k F, что
(v) = 1w1 … kwk = 1(v1) … k(vk) = (1v1+…+kvk).
Таким образом, (v – (1v1+…+kvk)) = 0V , т.е. v – (1v1+…+kvk) Ker() и поэтому найдутся такие 1 , … , s F, что
v – (1v1 + … + kvk ) = 1k1 + … + sks ,
т.е. v = 1v1 + … + kvk + 1k1 + … + sks , что и требовалось.
Теорема доказана.
Следствие 1 (о размерности пространства решений однородной системы). Пространство L решений однородной системы Ax = 0 m линейных уравнений с n неизвестными над полем F имеет размерность n – rg(A).
Доказательство. Рассмотрим линейный оператор : nF mF, заданный правилом (x) = Ax (x nF). Тогда Ker() = {x nF | Ax = 0} = L , а Im() = L((e1t) , … , (ent)), где e1t , … , ent – стандартный базис в nF , и по теореме dim nF = n = dim(Im()) + dim(Ker()). Поскольку (eit) = Aeit = = a(i), то dim(Im()) = dim L(a(1), … , a(n)) = rg(A), так что
dim L = dim(Ker()) = n – dim(Im()) = n – rg(A).
Следствие 1 доказано.
Следствие 2 (о рангах аннулирующих друг друга матриц). Для любых матриц A M(m, k, F), B M(k, n, F) со свойством AB = 0m n выполняется неравенство rg(A) + rg(B) k .
Доказательство. Столбцы матрицы В являются решениями однородной системы линейных уравнений Ax = 0. Поэтому rg(B) = dim L(b(1), … , b(n)) dim L = k – rg(A), что и требовалось доказать.
Следствие 2 доказано.